是否单射， 这个是函数的一个属性。
单射(injective)定义
单射函数（Injective Function）是指一种函数，它满足以下条件：
对于任意两个不同的输入值 x1 和 x2，如果 x1 ≠ x2，则函数的输出值 f(x1) 和 f(x2) 也必须不同，即 f(x1) ≠ f(x2)。
换句话说，单射函数是指一个函数，它将不同的输入值映射到不同的输出值。
公式定义：
∀x1,x2∈X, x1≠x2⇒f(x1)≠f(x2)\forall x_1, x_2 \in X, \ \ \ x1 ≠ x2 ⇒ f(x1) ≠ f(x2)∀x1,x2∈X, x1=x2⇒f(x1)=f(x2)
单射函数的一些例子
1. 常见的一次函数(线数)
下面这个函数 就是1个单射函数
f(x)=3x+1,x∈Rf(x) = 3x + 1 , x \in Rf(x)=3x+1,x∈R
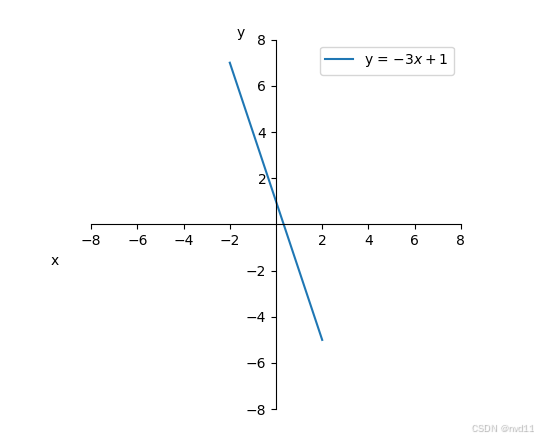
2. 3次函数
f(x)=x3+1,x∈Rf(x) = x^3 + 1, x \in Rf(x)=x3+1,x∈R
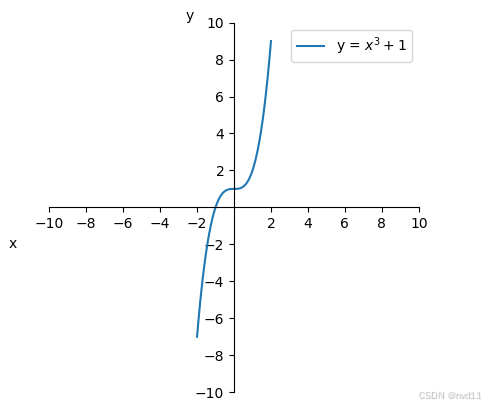
单射函数的主要特征
从函数图像大概可以得知， 单射函数随着x -> 增大， y的值是始终有个增加方向的， 从图像得知， 函数图像始终朝着1个方向， 要么向上， 要么向下， 不能回头。
但是这个特征不是绝对的， 只适用于连续的函数图像.
例如下面的单射函数就不符合上面的特征了
f(x)=1x,x∈R∧x≠0f(x) = \dfrac{1}{x}, x \in R \land x \neq 0f(x)=x1,x∈R∧x=0
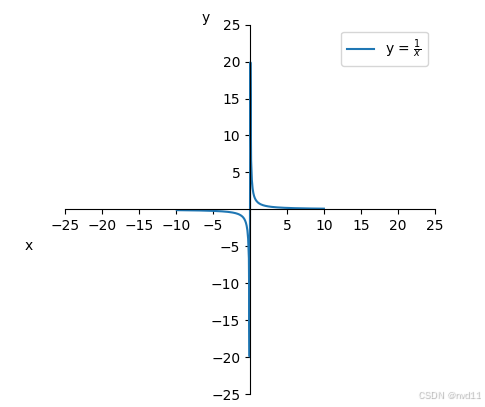
非单射函数的一些例子
1. 常函数
f(x)=3f(x) = 3f(x)=3
这种无论x 取什么值， y都是固定值， 在函数图像的展示就是1条直线， 违反了单数函数的定义
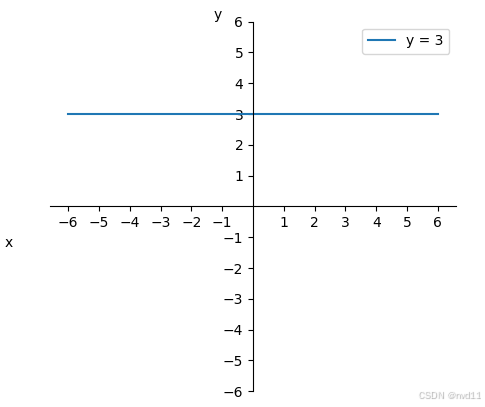
2. 二次函数(抛物线)
例子：
f(x)=x2−4f(x) = x^2 -4f(x)=x2−4
当x=−7x = -\sqrt{7}x=−7 或者 7\sqrt{7}7 时 f(x)的值 都等与3, 违反了单射函数的定义
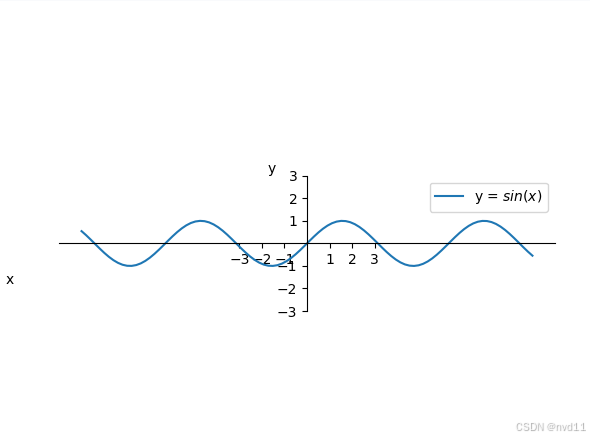
2. 正弦函数
f(x)=sin(x)f(x) = \sin(x)f(x)=sin(x)
更加明显了， 多个循环， 只要x 是 π\piπ的整数倍， f(x) 的值都是0
扫一扫
559
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
