刷题日记day6 (2025/11/19)

Acwing 1227. 分巧克力

解题思路:

        常规二分,主要要理解该巧克力边长,要(h[i]/n)*(w[i]/n)>k

代码

#include<iostream>
using namespace std;


const int N=1e5+10;
int h[N],w[N];
int n,k;

bool check(int mid){
    int num=0;
    for(int i=1;i<=n;i++){
        num+=(h[i]/mid)*(w[i]/mid);
        if (num>=k)return true;
    }
  
  return false;
}



int main(){
    
    
    cin>>n>>k;
    for(int i=1;i<=n;i++){
        cin>>h[i]>>w[i];
    }
    
    
    int l=1,r=1e5,mid;
    while(l<r){
        mid=l+r+1>>1;
        
        if(check(mid)){
            l=mid;
        }
        else{
            r=mid-1;            
        }
        
    }
    
    cout<<l;
    
    return 0;
}

Aciwng 795. 前缀和

解题思路

就是用一个Sn数组去装入a[1]到a[n]的和,方便后续查询访问(时间复杂度为1)

代码

#include<iostream>
using namespace std;

const int N=1e6+10;
int a[N],s[N];
int n,m,l,r;

//核心就是s[i]=s[i-1]+a[i]
//可以省去访问时要重复循坏累加
//预处理时间复杂度为On(n)
//查询时间复杂度可以降到On(1)


int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        cin>>a[i];
        s[i]=s[i-1]+a[i];
    }
    
    
    
    
    while(m--){
        cin>>l>>r;
        cout<<s[r]-s[l]+a[l]<<endl;
    }
    
    
    
    return 0;
}

Acwing 796. 子矩阵的和(二位前缀和)

解题思路

与一维相似,但要注意理清面积直接的关系,同时要记住 终点全包含起点前一行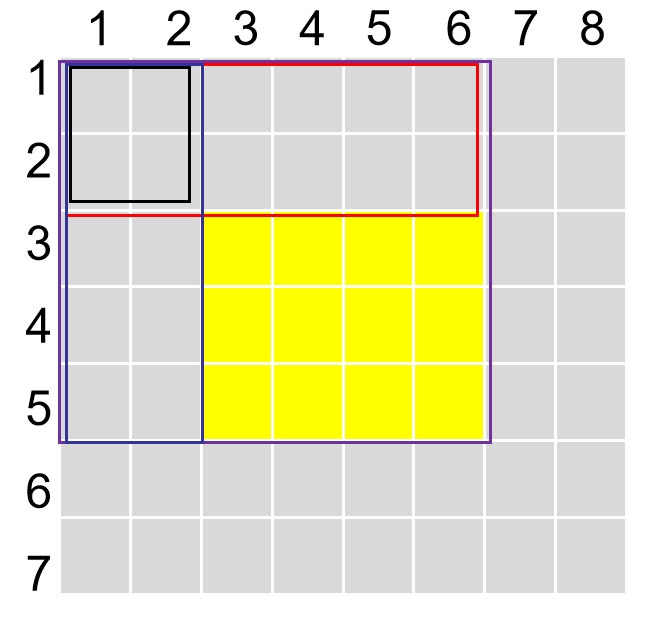

代码

#include<iostream>
using namespace std;

const int N=1000+10;

int a[N][N],s[N][N];
int n,m,q;

int main(){
    cin>>n>>m>>q;
    
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            cin>>a[i][j];
            
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
             s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];
    
    while(q--){
        int x1,x2,y1,y2;
        cin>>x1>>y1>>x2>>y2;
        //终点全包含，起点前一行
          cout << s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 - 1][y1 - 1] << endl;
    }
    
    return 0;
}