刷题日记day1 (2025/11/3)

acwing 95. 费解的开关(递归+二进制枚举)

问题描述

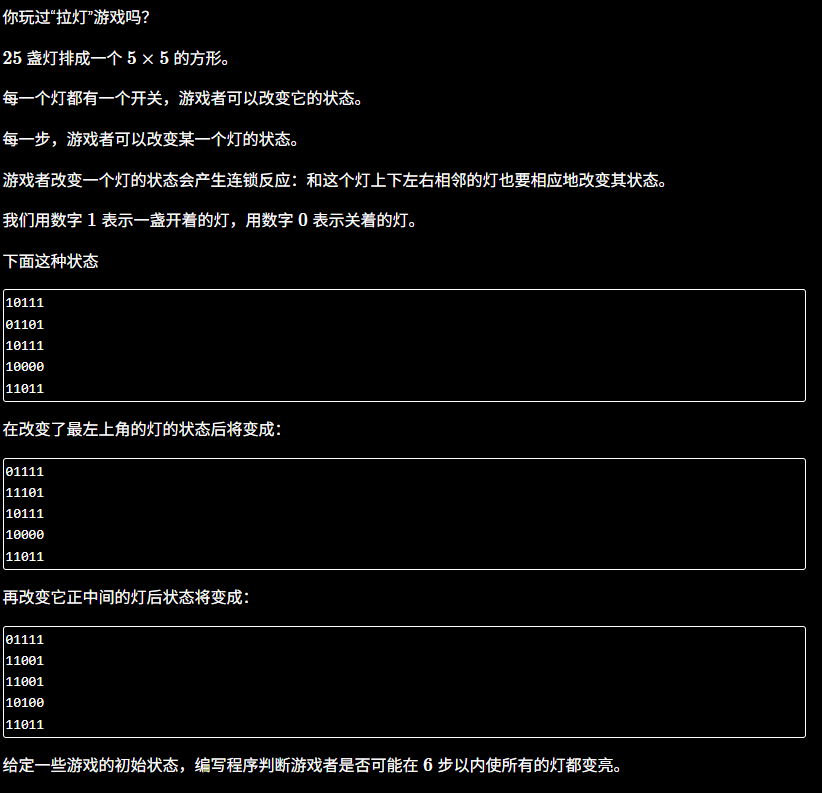
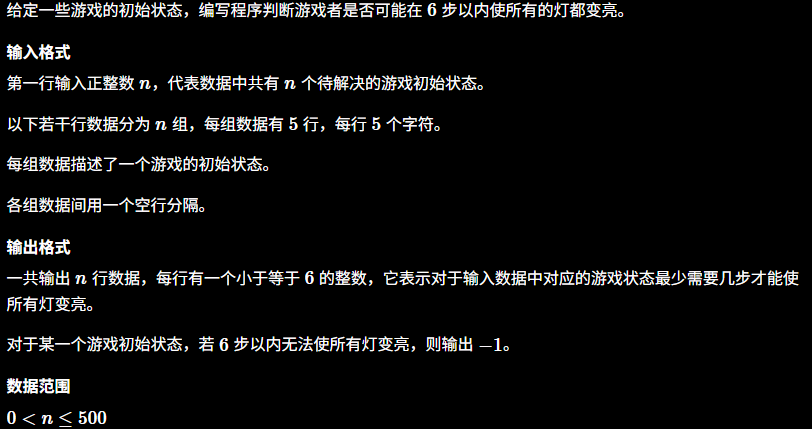
• 5×5的灯阵，每个灯有开(1)或关(0)两种状态

• 按一个灯会翻转它自己及上下左右相邻灯的状态

• 目标：最少步数让所有灯都亮起来

• 限制：最多6步，超过输出-1

解题思路

很明显要想改变灯的状态,就必须从它的下一层电亮,同理我们又不得不再次从他的下一层开始

继续点亮.

步骤1：枚举所有可能的第一行操作（32种）

步骤2：对每种方案，执行第一行预定操作

步骤3：递推处理第1-4行（修复灭的灯）

步骤4：检查最后一行是否全亮

步骤5：记录最小步数

之所以要进行步骤1而不直接进行步骤3,是因为可能会忽略一些看似多此一举操作的最优解.

🎯 算法总结

核心技巧

• 二进制枚举：处理小规模组合问题

• 递推思想：利用问题结构减少搜索空间

• 位运算：高效的状态操作

适用场景

• 开关灯类游戏

• 网格翻转问题

• 每个操作有局部影响的问题

• 问题规模适中（n ≤ 20）

解题过程

#include<iostream>
#include<cstring>
using namespace std;

int  n;
char g[5][5],backup[5][5];

//表示要切换电灯的自己,上,下,左,右
//在二维数组中：
//g[x][y]其中：
//x是行坐标（垂直方向）
//y是列坐标（水平方向）
int dx[5]={0,-1,1,0,0},dy[5]={0,0,0,-1,1};

//切换电灯状态
void turn(int x,int y){

    for(int i=0;i<5;i++){
        int a=x+dx[i],b=y+dy[i];
        
        if(a>=0&&a<5&&b>=0&&b<5)g[a][b]^=1;
    }
    
}

int solve(){
    
    
         int ant=10;
        
        //第一行按或不按,有2的五次方的方案
        for(int op=0;op<32;op++){
            //<cstring>中用来复制数组
            memcpy(g,backup,sizeof(backup));
            int step=0;
             bool success=true;
            //把第一行每一种可能都写出来(依靠此循环与op)
            for(int i=0;i<5;i++){
                
                //这里的是二进制枚举,1是按了没按,不是灯的状态
                //10101 最右边开始第i个是原本灯组左边第i个
                if(op>>i&1){
                    turn(0,i);
                    step++; }
            }
            
               //从第1行开始切换灯状态     
           for(int i=0;i<4;i++){
               for(int j=0;j<5;j++){
               if(g[i][j]=='0'){
                   turn(i+1,j);
                   step++;}
               }
           }         
                    
       
        
        for(int i=0;i<5;i++)
            if(g[4][i]=='0'){
            success=false;
            break;
            }
            
             if(success)ant=min(ant,step);
        }
        
      

            if(ant>6)return -1;
            return ant;
        

}

int main(){
    
    int n;
    cin>>n;
    
    while(n--){
        for(int i=0;i<5;i++)cin>>backup[i];
        cout<<solve()<<endl;
    }
    
    
    
    return 0;
}