Safe Trajectory Generation for Complex Urban Environments Using Spatio-Temporal Semantic Corridor

论文做了两个工作：一是环境中有动静态障碍物、红路灯、限速等不同类型的语义预算，使用统一的时空语义走廊进行建模，二是多数基于优化和Lattice的方法，只能在采样点保证无碰撞约束，使用分段贝塞尔曲线，在时空语义走廊内进行时空联合轨迹规划，保证整个轨迹的安全性。

1. 时空语义走廊

时空语义走廊是$slt$的$3D$空间，采用$Frenet$坐标系是因为，一是交通灯、限速等语义信息是和道路相关的，二是人类驾驶行为可以分为横向和纵向。采用$Frenet$的另一个好处，个人认为时空走廊的配置空间$sl$可以限制在一定范围内，如果使用笛卡尔坐标系，$xy$范围会有较大的变化，比如在高速路和城区的十字路口。

1.1 输入

• 地图；
• 动态障碍物预测轨迹；
• 参考车道；
• 初始解(粗解)；

时空走廊是基于初始解生成的，初始解由上游行为决策模型生产。

1.2 分类

• Obstacle-like semantic elements：比如动静态障碍物、红灯，会占据$slt$的三维空间；
• Constraint-like semantic elements：表示$slt$一个维度或者两个维度的约束，比如限速、换道时间等；

1.3 时空走廊生成

如算法$1$所示，时空走廊的生成包含四个步骤：seed generation (Line 3), cube inflation (Line 4), constraint association (Line 5) and cube relaxation (Line 6)。

1.3.1 seed generation

将行为决策和$ADC$初始状态映射在$slt$配置空间上，由于行为决策得到的初始解状态是离散的，因此时空走廊的可行性依赖于环境的复杂性和seed的分辨率($slt$的分辨率？)。为了保证可以生成时空走廊，就需要使两个相邻seed形成的cube是无碰撞的，当相邻两个seed形成的cube有碰撞，则时空走廊生成在此终止，也就是$ADC$要停在这个位置。

1.3.2 cube inflation

依次遍历seed，如果上一个已经膨胀处理过的cube已经包含这个seed，则跳过处理下一个seed。当前seed和上一个inflated cube的最后一个seed作为两个对角的顶点生成初始的cube，然后计算可以膨胀的方向，直到发生碰撞终止相应方向的碰撞，然后生成inflated cube。

膨胀方向的终止，一是进入Obstacle-like semantic elements范围，二是进入Constraint-like semantic elements范围。个人认为使每一个inflated cube都在一个Constraint-like semantic elements范围内，是为了在使用分段贝塞尔曲线进行轨迹优化时，使对应的分段的贝塞尔曲线的一阶导数约束更加容易处理。

由于后续的优化问题不对每一段轨迹(贝塞尔曲线)的行驶时间进行优化，因此相邻cube的在$t$轴上依次相连的，没有间断和重合部分。

1.3.3 cube relaxation

由于一些约束是软约束，例如换道时间等，为了使后续的优化问题有足够的解空间，膨胀后的cube需要使其在$s$和$l$方向上进行松弛，即相邻的cube在$s$和$l$方向有重合部分。

论文并没有对constraint association进行解释，个人认为时空走廊主要使求解cube，constraint association是将Constraint-like semantic elements作为附加的约束添加在相应的cube上。

论文对时空走廊计算的示例说明如下：

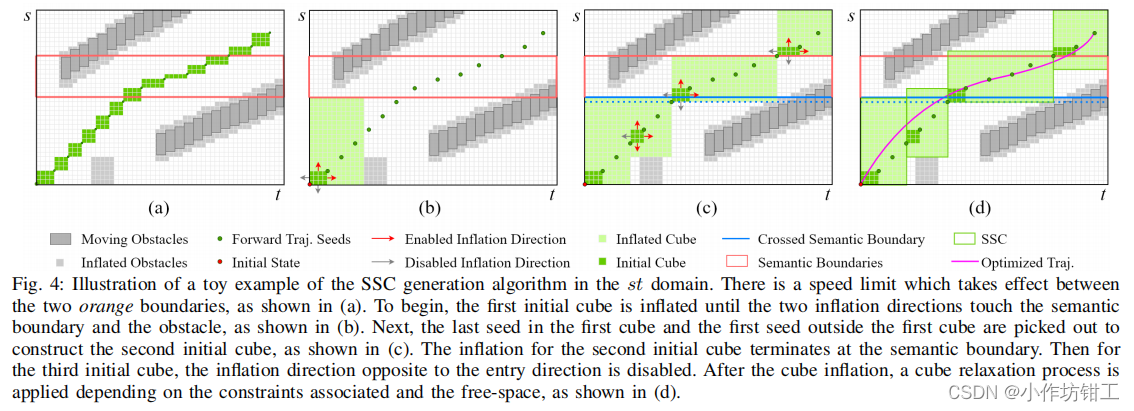
2. 轨迹生成

作者表述单个五次多项式曲线不能满足复杂场景下的轨迹规划，并且多项式形式曲线不能满足复杂的碰撞约束和动力学约束。而贝塞尔曲线由于其凸包性可以很好处理碰撞约束，而 hodograph property又可以很好的处理动力学约束，因此使用分段$5$阶贝塞尔曲线及逆行轨迹规划。

2.1 贝塞尔曲线性质

$m$阶贝塞尔曲线$f(t)$可以由$m+1$个控制点$p_i$在$t\in [0,1]$范围内插值表示：
$$f(t)=p_0{b}_m^0(t)+p_1$$