Spss离散的统计变量的显著性分析firedman，Wilcoxon

已于 2023-12-14 09:27:39 修改
阅读量5.5k 收藏 17
点赞数 3
CC 4.0 BY-SA版权
分类专栏： 数学与实验数据处理 文章标签： 人工智能
于 2018-09-23 15:39:18 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/moonlightpeng/article/details/82822325
本文详细介绍使用SPSS进行非参数检验的过程。首先利用Friedman test进行整体显著性分析，然后采用Wilcoxon符号秩测试进行两两比较。文章提供了具体的操作步骤和参数设置，帮助读者理解和应用这些统计方法。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

实验情况 是within三种或三种以上，且非参检验时先用firedam整体测试，再用wilcoxon两两测试

nSpss：对各调查问题下的数据整体采用firedman test进行显著性分析（ α=0.05 ），获得对应自由度下χ2和p

nSpss：采用Wilcoxo符号秩测试对各研究问题下不同实验条件进行两两分析（α=0.05 /n ，例如三种情况 0.05/C32=0.05/3=0.0167四种实验条件下， α=0.05 /C42=0.05/6），获得Z和p

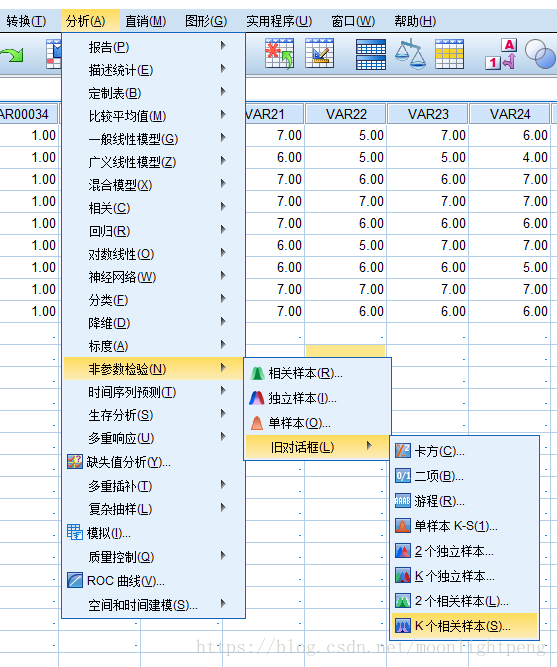
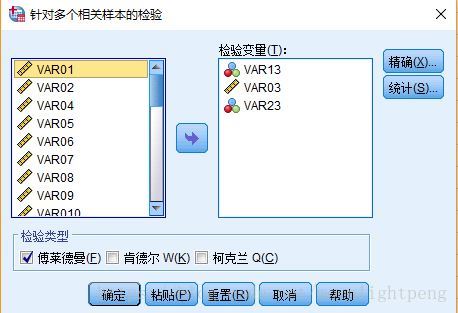
不同情况的每一个问题只能一个一个的整体分析

如果整体分析有差异则用Wilcoxo两两分析

0.05/Cn,m

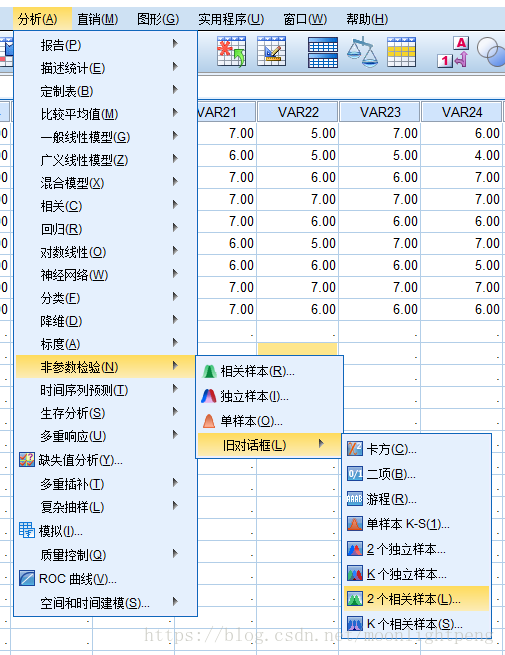
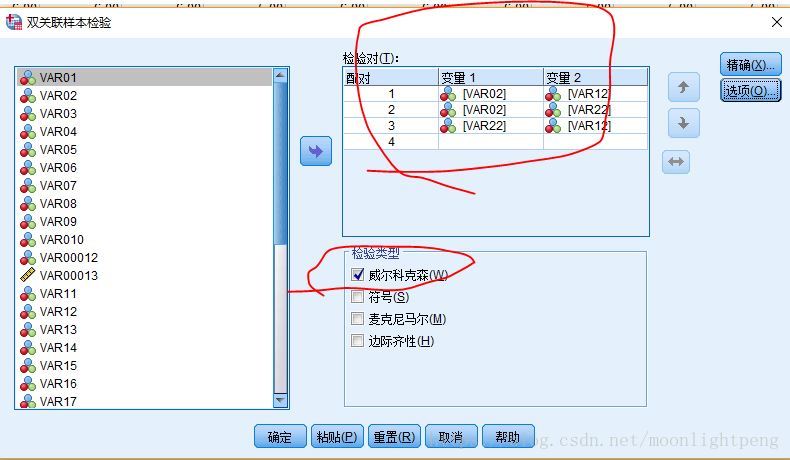
分析后如果描述参考SPSS官方文档

Friedman Test in SPSS Statistics

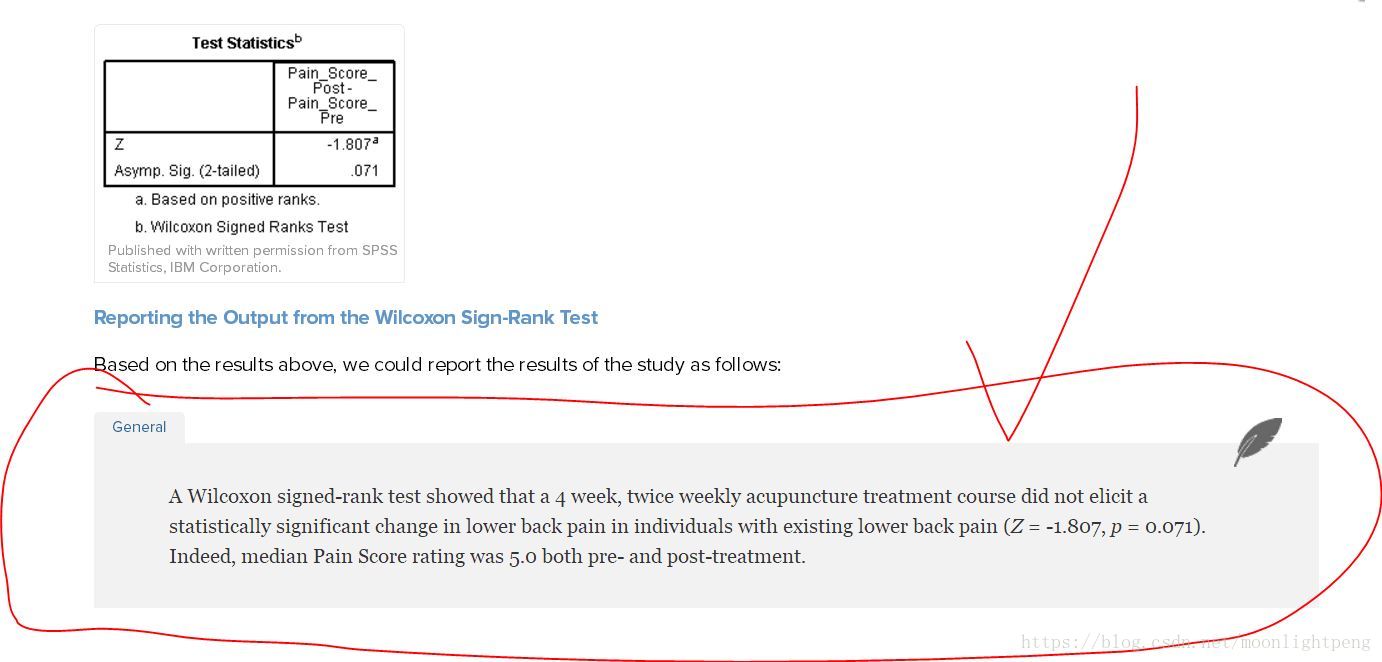
Wilcoxon Signed-Rank Test using SPSS Statistics

SPSS-两变量相关性分析（转）
dihong0615的博客
08-07 5074
两个变量之间存在确定性:关系和不确定关系（会存在一定的波动范围），就好比你的亲生母亲绝对只有一个，而你的亲叔叔可能有好几个（可以在1叔—4叔之间波动） 相关性一般分为 1：强正相关关系 （一个值会随着另一个值的增加而增加，增加幅度很明显） 2：弱正相关关系 （一个值会随着另一个值的增加而稍增加，增...
Prism和SPSS的显著性分析
liangjinghui123的博客
08-16 3748
Prism和SPSS的显著性分析
离散变量可不可以做方差分析_资料如何做统计分析
weixin_39722965的博客
12-05 1616
研究设计、资料搜集与整理分析是科学研究的三个紧密联系的阶段。在研究设计时要同时制订详尽的统计分析计划,以规范数据的管理和统计分析方法,使之与设计相匹配。事先无计划,或疏虞计划,在获取研究数据以后,多方计算,以求得研究者期待的结论,这样的事后分析(post hoc analysis)往往导致虚假结果。在研究过程中,统计分析计划允许修订或补充,但必须具有充足的理由。数据录入与数据库建立数据核...
多样本Friedman检验的具体示例和软件操作步骤
最新发布
SPSSAU的博客
06-24 423
假设SPSSAU(在线SPSS)输出的多样本Friedman检验结果显示P值小于0.05，说明4种剂量组雌性家兔子宫质量的总体分布存在显著性差异。进一步通过Nemenyi法多重比较，可以具体了解哪些剂量组之间存在差异。在某项随机区组设计的动物实验中，不同种系雌性家兔注射不同剂量雌激素后子宫质量（g）数据如下表所示。试比较4种剂量组雌性家兔子宫质量的差别有无统计学意义。多样本Friedman检验的具体示例和步骤。
SPSS--Friedman检验步骤
weixin_44549563的博客
09-26 2万+
一.Friedman检验原理 二.使用SPSS进行Friedman检验 步骤 操作 （1） 导入数据：以3X29维数据为例，即有三中对比数据，每个数据维29维 （2） 双击变量区域切换界面更改对比数据名称，改完名称后双击数字区域返回原始界面 （3） 数据检验，点击分析—非参数检验—旧对话框—K个相关样本 （4） 分别添加待检验数据到右侧数据框中，选择弗莱德曼，点击确定 （5） 数据生成 三.表格数据指
非参数检验——Wilcoxon 检验 & Friedman 检验与 Nemenyi 后续检验
qq_59747472的博客
04-15 7656
2​中第3 个元素的值都等于 5，且这 2 个 5 在整个序列中的排名分别是第 5 和第 6，因此这两个元素的排名为5 + 6 2 = 5.5 \frac{5+6}{2}=5.525+6​=5.5。在秩和检验中，我们不要求被检验的 2 组数据包含相同个数的元素，换句话说，秩和检验更适用于非成对数据之间的差异性检测。因而，与参数检验一样，非参数检验包括许多方法。首先需要得到每个算法在每个数据集上的测试结果，可以是准确率，也可以是均方误差，然后在每个数据上根据测试性能的好坏进行排序，并赋予序值 1，2，…
spss之数据处理（离散化）
yuandebaba的博客
08-23 7977
把无限空间有限个体映射到有限空间里有限白话：在不改变数据相对大小的条件下，对数据进行相对的缩小例如：原数据：7 1 4 3 处理后： 4 1 3 2原数据：{100,250}{200,400} 处理后{1,3}{2,4}
在SPSS里用Duncan法进行多组样本间差异显著性分析.doc
09-30
SPSS 是一种常用的统计分析软件，在 SPSS 中可以使用 Duncan 法进行多组样本间差异显著性分析。 Duncan 法的优点是可以对多个样本之间的均值进行比较，并可以确定每对样本之间的差异是否显著。该方法可以避免多重...
问卷数据分析|SPSS之分类变量描述性统计
Hou556的博客
02-06 1153
1.点击分析--描述统计--频率2. 选中分类变量，点击中间箭头3.图表选中条形图，图表值选择百分比，选择确定4.这里显示出了描述性统计的结果5.下面就是图形，但SPSS画的图形都不是很好啊看，建议用其他软件画图（饼图或者条形图可看案例）
SPSS - 显著性分析 一般线性模型的单因素与多因素选择
热门推荐
Poisson_SHAN的博客
10-23 2万+
SPSS中可以使用分析-一般线性模型中的分析来做显著性分析 其中又有两个选择，单因素与多因素。 查看SPSS官方帮助文档，即点击左下角的“？”，找到了两者区别。 单因素 https://www.ibm.com/support/knowledgecenter/zh/SSLVMB_25.0.0/statistics_mainhelp_ddita/spss/base/idh_glmu.html “GLM 单变量”过程通过一个或多个因子和/或变量，为一个因变量提供回归分析和方差分析。因子变量将总体划分成组。通过使
四台机器生产同一个产品差异性检验.rar_数理统计分析_显著性差异
09-23
在数理统计分析中，显著性差异检验是一个重要的概念，用于判断多个样本群体之间是否存在显著的差别。在这个案例中，我们关注的是四台机器在生产同一产品时的日产量差异。假设每台机器的日产量服从正态分布，并且它们...
SPSS-Friedman 秩和检验-非参数检验-K个相关样本检验 案例解析
moonlightpeng的博客
09-23 9255
SPSS-Friedman 秩和检验-非参数检验-K个相关样本检验 案例解析
SPSS如何做离散和连续变量的统计描述
可乐联盟
08-07 6464
SPSS如何做离散和连续变量的统计描述 离散变量的统计描述 原始数据 §频数列表 §百分比 §累计频数 §累计百分比 集中趋势 §众数 连续变量的统计描述 频数表 操作步骤：确定组数；确定组距；确定各组段的上下限 各步骤的操作都存在着一些主观性，但因为只是进行初步的观察，这并无大碍 是一种非常直观的方法，但比较粗糙，如果希望进行深入的分析，则必须要使用一些严谨的...
统计学_显著性检验综述
YoungGy的专栏
08-23 1万+
参数检验 非参数检验
随机变量-离散-连续-假设检验方法
gao_的博客
04-10 4392
一组随机样本数据需要进行分析处理时，往往需要用到假设检验，对于离散变量discrete多用卡方检验，连续变量continuous用t检验或wilcoxon秩序和检验，具体的的使用场景如下 离散变量-卡方检验-适用条件 四格表： 所有的理论数T≥5并且总样本量n≥40，用卡方进行检验 理论数T＜5但T≥1并且n≥40，用连续性校正的卡方进行检验 有理论数T＜1或n＜40，用Fisher’s检验 ...
显著性测试（Friedman test, Post-hoc Nimenyi test以及可视化）
MasterQKK
04-02 1万+
Friedman test， Post-hoc Nimenyi test，结果可视化， rank Critical difference，H0 hypothesis， 显著性测试
统计学指南
Debroon
06-25 7241
文章目录为什么要学习统计学图表的玄机被混淆的因果关系打破权威数据分析必备统计小百科概率和机会变量和常量数据的几种类型易混淆的统计术语描述统计：图表描述定类数据的图表描述定序数据的图表描述定距数据的图表描述多变量数据的图表描述如何选择合适的图表有效图表的的几个基本要素增强图表达力的几种方法可视化图表的几个注意事项描述统计：统计量描述集中趋势：数据分布特征的描述离中趋势：数据分布特征的描述偏态和峰态：数据分布特征的描述数据标准化的几种方法抽样数据的收集和整理收集数据是的误差常用的抽样方法设计调查问卷的原则推断.
机器学习系列—深入探索弗里德曼检验：非参数统计分析的利器
u013889591的专栏
08-16 2766
在数据分析领域，我们经常遇到需要比较多个相关样本均值的场景。当数据不符合正态分布或方差齐性时，传统的方差分析（ANOVA）就不再适用。这时，非参数统计方法就显得尤为重要，其中弗里德曼检验（Friedman test）就是一种用于多个相关样本比较的非参数检验方法。弗里德曼检验作为一种强大的非参数统计工具，为我们提供了一种在不满足传统参数检验条件下分析数据的方法。它简单、易于实现，并且可以提供关于数据分布和组间差异的宝贵信息。在实际应用中，我们应该根据数据的特性和研究目的选择合适的统计方法。
SPSS单变量双因素方差分析显著性
04-15
<think>嗯，用户想了解如何在SPSS中进行单变量双因素方差分析的显著性检验和结果解释。首先，我需要回忆一下单变量双因素方差分析的基本概念，确保自己理解正确。根据引用内容，单变量方差分析指的是只有一个因变量，但自变量（因子）可以有多个，这里的双因素就是两个自变量。 接下来，用户需要的是具体的步骤和结果解释。我应该参考提供的引用资料，尤其是引用[3]提到了双因素重复测量方差分析，不过用户的问题可能更侧重于普通的双因素方差分析，而不是重复测量。但引用[1]和[2]主要讨论单因素和一般线性模型，可能需要结合这些内容。 首先，SPSS中进行方差分析一般有两种途径：比较均值里的单因素Anova和一般线性模型中的单变量分析。双因素的话应该使用一般线性模型，因为单因素Anova只能处理一个自变量。所以步骤应该是进入“分析”->“一般线性模型”->“单变量”。 然后，需要设置因变量、固定因子（两个自变量），可能还有随机因子，但用户的问题可能只涉及固定因子。接下来，模型设定，通常保持全因子模型，除非有特殊需求。事后检验（两两比较）如果因子水平超过两个，可能需要选择比如Tukey或Bonferroni方法。 在结果解释方面，首先看主效应和交互效应的显著性。如果交互效应显著，可能需要进一步简单效应分析，但SPSS默认输出可能不包含这个，需要通过语法或其他设置。然后，查看各因子的F值和p值，判断是否拒绝原假设。同时，效应量如偏η²可以帮助了解影响程度。 用户可能还会关心如何判断数据是否符合方差分析的前提条件，比如方差齐性和正态性。需要提醒他们进行Levene检验和正态性检验，必要时进行数据转换或使用非参数方法。 此外，引用[2]中的单因素方差分析步骤可能部分适用，比如数据文件的建立和变量选择，但双因素需要更多设置。需要确保用户正确区分单因素和双因素的操作差异。 最后，常见问题如交互作用不显著时的处理，或者主效应显著但交互效应不显著时的解释，也需要简要提及。可能还需要指导用户如何报告结果，包括F值、自由度、p值和效应量。 总结步骤：准备数据，选择分析菜单，设置变量，模型选项，事后检验，结果解读。同时注意前提条件检验和结果报告的完整性。</think>### SPSS单变量双因素方差分析显著性检验步骤与解释 #### 一、操作步骤 1. **数据准备** - 确保数据满足方差分析前提条件： - **独立性**：样本独立 - **正态性**：因变量在各因子组合下近似正态分布（可通过Q-Q图或Shapiro-Wilk检验验证） - **方差齐性**：各组方差相等（通过Levene检验判断）[^2][^3] - 数据结构：包含一个**因变量**（连续变量）和两个**分类自变量**（因子）。 2. **菜单操作** - 点击 `分析(Analyze)` → `一般线性模型(General Linear Model)` → `单变量(Univariate)`[^1][^3]。 - 将因变量放入 **因变量(Dependent Variable)** 框，两个分类变量放入 **固定因子(Fixed Factors)** 框（若因子为随机效应，需放入 **随机因子(Random Factors)**）[^1]。 3. **模型设置** - 在 **模型(Model)** 选项卡中： - 选择 **全因子(Full Factorial)** 以分析主效应和交互效应。 - 若需自定义模型（如忽略交互项），选择 **设定(Custom)** 并手动添加因子主效应[^1][^3]。 4. **事后检验（可选）** - 在 **事后比较(Post Hoc)** 选项卡中，若因子水平数≥3且主效应显著，选择Tukey、Bonferroni等方法进行两两比较。 5. **选项设置** - 勾选 **描述统计(Descriptive Statistics)**、**效应量估计(Estimates of Effect Size)** 和 **方差齐性检验(Homogeneity Tests)**[^3]。 --- #### 二、结果解读 1. **方差齐性检验** - 查看 **Levene检验**结果： - 若 *p > 0.05*，满足方差齐性假设，可继续分析。 - 若 *p ≤ 0.05*，需使用稳健方法（如Welch校正）或数据转换[^2][^3]。 2. **显著性检验** - 主表 **主体间效应检验(Tests of Between-Subjects Effects)**： - **主效应**：分别查看两个因子的 *F值* 和 *显著性(p值)*。 示例：若因子A的 *p < 0.05*，说明其主效应显著。 - **交互效应**：检查因子A×因子B的交互项。 若交互项显著（*p < 0.05*），需进一步分析简单效应（需手动编写语法或使用EMmeans插件）[^1][^3]。 - **效应量**：偏η²（Partial Eta Squared）表示因子解释的方差比例，值越大影响越强（一般≥0.01为小效应，≥0.06为中效应，≥0.14为大效应）[^1]。 3. **事后比较结果** - 若主效应显著且因子水平数≥3，查看事后检验表（如Tukey HSD），判断具体哪些组间差异显著。 --- #### 三、示例报告格式 ```text 双因素方差分析显示，因子A对因变量影响显著，F(自由度A, 误差自由度)=F值, p=0.012，偏η²=0.15；因子B主效应不显著（p=0.32）。因子A与B交互作用显著，F(交互自由度, 误差自由度)=5.67, p=0.003，偏η²=0.08。进一步简单效应分析表明，当因子B为水平1时，因子A的效应显著（p<0.05）。 ``` --- ####
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值