机器学习算法梳理—决策树

最新推荐文章于 2023-12-19 14:50:48 发布

原创最新推荐文章于 2023-12-19 14:50:48 发布 · 373 阅读

0 ·

CC 4.0 BY-SA版权

机器学习专栏收录该内容

14 篇文章

订阅专栏

本文深入探讨了决策树的基础，包括信息论概念如信息、熵、条件熵、信息增益和基尼不纯度。接着介绍了ID3算法的原理和过程，及其优缺点。C4.5作为ID3的改进版，采用了信息增益比。CART算法用于分类和回归，基于基尼指数或平方误差最小化准则。连续和离散特征的处理方法也得到了讨论，如z-score和max-min标准化。最后，文章提到了sklearn库在决策树中的参数设置，并提供了Python绘制决策树的参考文献。

一、信息论基础

1.信息定义

如果待分类的事务可能划分在多个分类之中，则信息定义为：
在这里插入图片描述
其中，xi 表示第 i 个分类，p(xi) 表示选择第 i 个分类的概率。
其中，n 表示分类的数量。

2.熵

熵定义为信息的期望值。熵是用来衡量一个系统混乱程度的物理量，代表一个系统中蕴含多少信息量，信息量越大表明一个系统不确定性就越大，就存在越多的可能性。熵值越大，则随机变量的不确定性就越大。假如有变量X，其可能的分类有n种，熵，可以通过下面的公式得到：
在这里插入图片描述
其中Pi是变量出现的概率。一个事物内部会存在随机性，也就是不确定性，而从外部消除这个不确定性唯一的办法是引入信息。如果没有信息，任何公式或者数字的游戏都无法排除不确定性。

2. 条件熵

表示在直到某一条件后，某一随机变量的复杂性或不确定性。**知道的信息越多，随机事件的不确定性就越小。**定义如下：
在这里插入图片描述

3.联合熵

设X Y为两个随机变量，对于给定条件Y=y下，X的条件熵定义为：
在这里插入图片描述

4.信息增益

信息增益（information gain）指的是划分数据集前后信息发生的变化。表示得知特征X的信息而使得类Y的信息的不确定性减少的程度。特征A对训练数据集D的信息增益g(D,A)，定义为集合D的经验熵H(D)与特征A给定条件下D的经验条件熵H(D|A)之差，即：
在这里插入图片描述
熵H(Y)与条件熵H(Y|X)之差称为互信息(mutual information)

5.基尼不纯度

从一个数据集中随机选取子项，度量其被错误的划分到其他组里的概率。一个随机事件变成它的对立事件的概率。计算公式：(fi为某概率事件发生的概率)
在这里插入图片描述

二、ID3算法

1.原理

ID3算法（interative dichotomiser 3）的核心是在决策树各个结点上应用信息增益准则选择特征，递归地构建决策树。具体方法是：从根结点（root node）开始，对结点计算所有可能的特征的信息增益，选择信息增益最大的特征作为结点的特征，由该特征的不同取值建立子结点；再对子结点递归地调用以上方法，构建决策树；直到所有特征的信息增益均很小或没有特征可以选择为止。最后得到一个决策树。相当于用极大似然法进行概率模型的选择。

2.过程

在这里插入图片描述

3.优缺点

ID3算法只有树的生成，所以该算法生成的树容易产生过拟合。

三、C4.5算法

1.原理

C4.5算法与 ID3 算法极为相似，只是在特征选择上有所不同，算是一种对 ID3 算法的改进了。C4.5算法在决策树生成过程中，用信息增益比来选择特征。

2.过程

在这里插入图片描述

四、CART分类树

1.原理

分类与回归树(classification and regression tree, CART)模型同样由特征选择、树的生成及剪枝组成，既可以用于分类也可以用于回归。 CART算法由以下两步组成
(1)决策树生成：基于训练数据集生成决策树，牛成的决策树要尽量大；
(2)决策树剪枝：用验证数据集对己生成的树进行剪枝并选择最优子树，这时用损失函数最小作为剪枝的标准。
CART生成：对回归树用平方误差最小化准则，对分类树用基尼指数(Gini index)最小化准则，进行特征选择。

2.过程

（1）回归树的生成

在这里插入图片描述

（2）分类树的生成

分类树用基尼指数选择最优特征，同时决定该特征的最优二值切分点.

五、连续特征和离散特征处理

1.连续特征：

**z-score标准化：**这是最常见的特征预处理方式，基本所有的线性模型在拟合的时候都会做 z-score标准化。具体的方法是求出样本特征x的均值mean和标准差std，然后用（x-mean)/std来代替原特征。这样特征就变成了均值为0，方差为1了。在sklearn中，我们可以用StandardScaler来做z-score标准化。当然，如果我们是用pandas做数据预处理，可以自己在数据框里面减去均值，再除以方差，自己做z-score标准化。
**max-min标准化：**也称为离差标准化，预处理后使特征值映射到[0,1]之间。具体的方法是求出样本特征x的最大值max和最小值min，然后用(x-min)/(max-min)来代替原特征。如果我们希望将数据映射到任意一个区间[a,b]，而不是[0,1]，那么也很简单。用(x-min)(b-a)/(max-min)+a来代替原特征即可。在sklearn中，我们可以用MinMaxScaler来做max-min标准化。这种方法的问题就是如果测试集或者预测数据里的特征有小于min，或者大于max的数据，会导致max和min发生变化，需要重新计算。所以实际算法中，除非你对特征的取值区间有需求，否则max-min标准化没有 z-score标准化好用。
**L1/L2范数标准化：**如果我们只是为了统一量纲，那么通过L2范数整体标准化也是可以的，具体方法是求出每个样本特征向量x的L2范数||x||2||x||2,然后用x / ||x||2x/||x||2代替原样本特征即可。当然L1范数标准化也是可以的，即用x / ||x||1x/||x||1代替原样本特征。通常情况下，范数标准化首选L2范数标准化。在sklearn中，我们可以用Normalizer来做L1/L2范数标准化。

2.离散特征：

对于离散的特征基本就是按照one-hot编码，该离散特征有多少取值，就用多少维来表示该特征。
（1）使用one-hot编码，将离散特征的取值扩展到了欧式空间，离散特征的某个取值就对应欧式空间的某个点。
（2）将离散特征通过one-hot编码映射到欧式空间，是因为，在回归，分类，聚类等机器学习算法中，特征之间距离的计算或相似度的计算是非常重要的，而我们常用的距离或相似度的计算都是在欧式空间的相似度计算，计算余弦相似性，基于的就是欧式空间。
（3）将离散型特征使用one-hot编码，确实会让特征之间的距离计算更加合理。比如，有一个离散型特征，代表工作类型，该离散型特征，共有三个取值，不使用one-hot编码，其表示分别是x1=(1),x2=(2),x3=(3)x1=(1),x2=(2),x3=(3)。两个工作之间的距离是，(x1,x2)=1,d(x2,x3)=1,d(x1,x3)=2(x1,x2)=1,d(x2,x3)=1,d(x1,x3)=2。那么x1x1和x3x3工作之间就越不相似吗？显然这样的表示，计算出来的特征的距离是不合理。那如果使用one-hot编码，则得到x1=(1,0,0),x2=(0,1,0),x3=(0,0,1)x1=(1,0,0),x2=(0,1,0),x3=(0,0,1)，那么两个工作之间的距离就都是sqrt(2)sqrt(2).即每两个工作之间的距离是一样的，显得更合理
（4）离散特征进行one-hot编码后，编码后的特征，其实每一维度的特征都可以看做是连续的特征。就可以跟对连续型特征的归一化方法一样，对每一维特征进行归一化。比如归一化到[-1,1]或归一化到均值为0,方差为1

七、sklearn参数详解

sklearn.tree.DecisionTreeClassifier
        (criterion='gini', splitter='best', max_depth=None, min_samples_split=2, 
        min_samples_leaf=1,min_weight_fraction_leaf=0.0, max_features=None, 
        random_state=None, max_leaf_nodes=None, min_impurity_decrease=0.0, 
        min_impurity_split=None, class_weight=None, presort=False)

criterion:特征选择的标准，有信息增益和基尼系数两种，使用信息增益的是ID3和C4.5算法（使用信息增益比），使用基尼系数的CART算法，默认是gini系数。

splitter:特征切分点选择标准，决策树是递归地选择最优切分点，spliter是用来指明在哪个集合上来递归，有“best”和“random”两种参数可以选择，best表示在所有特征上递归，适用于数据集较小的时候，random表示随机选择一部分特征进行递归，适用于数据集较大的时候。

max_depth:决策树最大深度，决策树模型先对所有数据集进行切分，再在子数据集上继续循环这个切分过程，max_depth可以理解成用来限制这个循环次数。

min_samples_split:子数据集再切分需要的最小样本量，默认是2，如果子数据样本量小于2时，则不再进行下一步切分。如果数据量较小，使用默认值就可，如果数据量较大，为降低计算量，应该把这个值增大，即限制子数据集的切分次数。

min_samples_leaf:叶节点（子数据集）最小样本数，如果子数据集中的样本数小于这个值，那么该叶节点和其兄弟节点都会被剪枝（去掉），该值默认为1。

min_weight_fraction_leaf:在叶节点处的所有输入样本权重总和的最小加权分数，如果不输入则表示所有的叶节点的权重是一致的。

max_features:特征切分时考虑的最大特征数量，默认是对所有特征进行切分，也可以传入int类型的值，表示具体的特征个数；也可以是浮点数，则表示特征个数的百分比；还可以是sqrt,表示总特征数的平方根；也可以是log2，表示总特征数的log个特征。

random_state:随机种子的设置，与LR中参数一致。

max_leaf_nodes:最大叶节点个数，即数据集切分成子数据集的最大个数。

min_impurity_decrease:切分点不纯度最小减少程度，如果某个结点的不纯度减少小于这个值，那么该切分点就会被移除。

min_impurity_split:切分点最小不纯度，用来限制数据集的继续切分（决策树的生成），如果某个节点的不纯度（可以理解为分类错误率）小于这个阈值，那么该点的数据将不再进行切分。

class_weight:权重设置，主要是用于处理不平衡样本，与LR模型中的参数一致，可以自定义类别权重，也可以直接使用balanced参数值进行不平衡样本处理。

presort:是否进行预排序，默认是False，所谓预排序就是提前对特征进行排序，我们知道，决策树分割数据集的依据是，优先按照信息增益/基尼系数大的特征来进行分割的，涉及的大小就需要比较，如果不进行预排序，则会在每次分割的时候需要重新把所有特征进行计算比较一次，如果进行了预排序以后，则每次分割的时候，只需要拿排名靠前的特征就可以了。

八、Python绘制决策树

本文所用的数据如下：
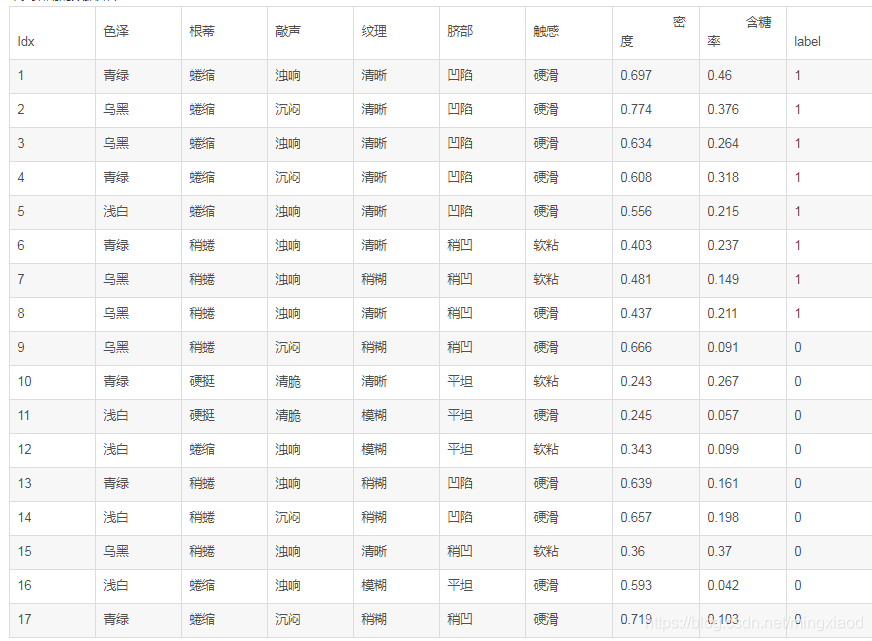
在这里插入图片描述
将中文字符全换成了英文，如下：

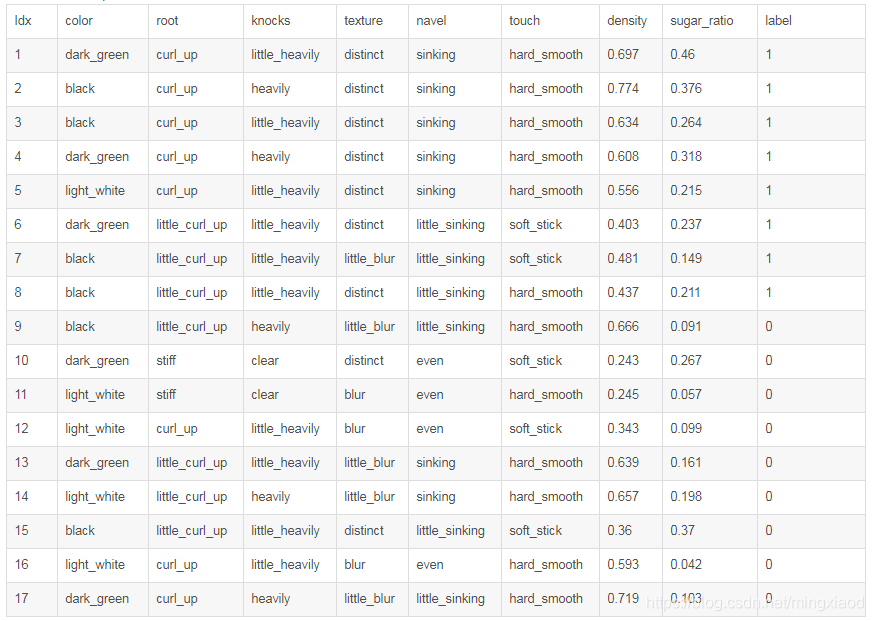
# -*- coding: utf-8 -*-
"""
Created on Wed Sep 27 14:52:51 2017
@author: Administrator
"""
 
import matplotlib.pyplot as plt  
decisionNode=dict(boxstyle="sawtooth",fc="0.8")  
leafNode=dict(boxstyle="round4",fc="0.8")  
arrow_args=dict(arrowstyle="<-")  
  
  
#计算树的叶子节点数量  
def getNumLeafs(myTree):  
    numLeafs=0  
    firstStr=myTree.keys()[0]  
    secondDict=myTree[firstStr]  
    for key in secondDict.keys():  
        if type(secondDict[key]).__name__=='dict':  
            numLeafs+=getNumLeafs(secondDict[key])  
        else: numLeafs+=1  
    return numLeafs  
  
#计算树的最大深度  
def getTreeDepth(myTree):  
    maxDepth=0  
    firstStr=myTree.keys()[0]  
    secondDict=myTree[firstStr]  
    for key in secondDict.keys():  
        if type(secondDict[key]).__name__=='dict':  
            thisDepth=1+getTreeDepth(secondDict[key])  
        else: thisDepth=1  
        if thisDepth>maxDepth:  
            maxDepth=thisDepth  
    return maxDepth  
  
#画节点  
def plotNode(nodeTxt,centerPt,parentPt,nodeType):  
    createPlot.ax1.annotate(nodeTxt,xy=parentPt,xycoords='axes fraction',xytext=centerPt,textcoords='axes fraction',va="center", ha="center",bbox=nodeType,arrowprops=arrow_args) 
      
    
  
#画箭头上的文字  
def plotMidText(cntrPt,parentPt,txtString):  
    lens=len(txtString)  
    xMid=(parentPt[0]+cntrPt[0])/2.0-lens*0.002  
    yMid=(parentPt[1]+cntrPt[1])/2.0  
    createPlot.ax1.text(xMid,yMid,txtString)  
      
def plotTree(myTree,parentPt,nodeTxt):  
    numLeafs=getNumLeafs(myTree)  
    depth=getTreeDepth(myTree)  
    firstStr=myTree.keys()[0]  
    cntrPt=(plotTree.x0ff+(1.0+float(numLeafs))/2.0/plotTree.totalW,plotTree.y0ff)  
    plotMidText(cntrPt,parentPt,nodeTxt)  
    plotNode(firstStr,cntrPt,parentPt,decisionNode)  
    secondDict=myTree[firstStr]  
    plotTree.y0ff=plotTree.y0ff-1.0/plotTree.totalD  
    for key in secondDict.keys():  
        if type(secondDict[key]).__name__=='dict':  
            plotTree(secondDict[key],cntrPt,str(key))  
        else:  
            plotTree.x0ff=plotTree.x0ff+1.0/plotTree.totalW  
            plotNode(secondDict[key],(plotTree.x0ff,plotTree.y0ff),cntrPt,leafNode)  
            plotMidText((plotTree.x0ff,plotTree.y0ff),cntrPt,str(key))  
    plotTree.y0ff=plotTree.y0ff+1.0/plotTree.totalD  
  
def createPlot(inTree):  
    fig=plt.figure(1,facecolor='white')  
    fig.clf()  
    axprops=dict(xticks=[],yticks=[])  
    createPlot.ax1=plt.subplot(111,frameon=False,**axprops)  
    plotTree.totalW=float(getNumLeafs(inTree))  
    plotTree.totalD=float(getTreeDepth(inTree))  
    plotTree.x0ff=-0.5/plotTree.totalW  
    plotTree.y0ff=1.0  
    plotTree(inTree,(0.5,1.0),'')  
    plt.show() 
###############测试代码
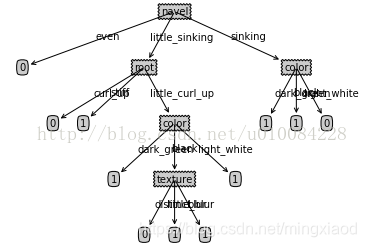
tree={'navel': {'even': 0L,
  'little_sinking': {'root': {'curl_up': 0L,
    'little_curl_up': {'color': {'black': {'texture': {'blur': 1L,
        'distinct': 0L,
        'little_blur': 1L}},
      'dark_green': 1L,
      'light_white': 1L}},
    'stiff': 1L}},
  'sinking': {'color': {'black': 1L, 'dark_green': 1L, 'light_white': 0L}}}}
createPlot(tree)

结果
在这里插入图片描述