一、相关概念
1.先验概率
在贝叶斯统计中,某一不确定量p的先验概率分布是在考虑”观测数据”前,能表达p不确定性的概率分布。它旨在描述这个不确定量的不确定程度,而不是这个不确定量的随机性。可以是基于历史数据的统计,可以由背景常识得出,也可以是人的主观观点给出。一般都是单独事件概率,如P(x),P(y)。
2.后验概率
在贝叶斯统计中,一个随机事件或者一个不确定事件的后验概率是在考虑和给出相关证据或数据后所得到的条件概率。同样,后验概率分布是一个未知量(视为随机变量)基于试验和调查后得到的概率分布。或者说是基于先验概率求得的反向条件概率,与条件概率形式相同。
贝叶斯公式:
P(y|x) = ( P(x|y) * P(y) ) / P(x)
其中:
P(y) 是先验概率,一般都是人主观给出的。贝叶斯中的先验概率一般特指它。
P(x|y) 是条件概率,又叫似然概率,一般是通过历史数据统计得到。一般不把它叫做先验概率,但从定义上也符合先验定义。
P(y|x) 是后验概率,一般是我们求解的目标。(已知x的前提下,然后求y发生的概率)
P(x) 其实也是先验概率,只是在贝叶斯的很多应用中不重要(因为只要最大后验不求绝对值),需要时往往用全概率公式计算得到。
3. 似然概率
(1) 常说的概率是指给定参数后,预测即将发生的事件的可能性。拿硬币这个例子来说,我们已知一枚均匀硬币的正反面概率分别是0.5,要预测抛两次硬币都朝上的概率:
H代表Head,表示头朝上
p(HH | pH = 0.5) = 0.5*0.5 = 0.25.
这种写法其实有点误导,后面的这个p其实是作为参数存在的,即p概率的值相当于未知参数(可以取p=0.4/0.5/0.6等等),它而不是一个随机变量,因此不能写成是条件概率形式,条件概率中都属于随机变量,更靠谱的写法应该是 p(HH;p=0.5)。
(2) 似然概率正好与这个过程相反,我们关注的量不再是事件的发生概率,而是已知发生了某些事件,我们希望知道参数应该是多少。
例如:现在我们已经抛了两次硬币,并且知道了结果是两次头朝上(HH),现在,我们希望通过这个结果算出这枚硬币抛出去正面朝上的概率为0.5的概率是多少?(这个事件能使P=0.5发生的概率),正面朝上的概率为0.8的概率是多少?(这个事件能使P=0.8发生的概率)
求解这两个的概率就叫做似然函数,可以说成是通过事件的结果对某一个参数(p)的猜想的概率,这样表示成(条件)概率就是
**L**(pH=0.5|HH) =P(pH=0.5|HH) = P(pH=0.5,HH)/P(HH);既然HH是已经发生的事件,理所当然P(HH) = 1
所以:**P(pH=0.5|HH) = P(pH=0.5,HH) = P(HH;pH=0.5)**
所以,我们可以safely得到:
L(pH=0.5|HH) = P(HH|pH=0.5) = 0.5*0.5=0.25.
这个0.25的意思是,在已知抛出两个正面的情况下,pH = 0.5的概率等于0.25。
再算一下
L(pH=0.6|HH) = P(HH|pH=0.6) = 0.6*0.6=0.36.
…
把pH从0~1的取值所得到的似然函数的曲线画出来得到这样一张图:
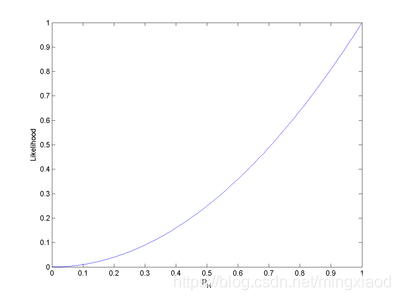
可以发现,pH = 1时似然函数(概率)是最大的。即L(pH = 1|HH) = 1。
即使得似然函数最大的参数是p=1,相当于最大化似然函数所对应的参数p.
那么最大似然概率的问题也就好理解了。
最后:回到这个硬币的例子上来,在观测到结果为HH的情况下,pH = 1是最合理的,即可估计在未抛掷硬币之前,硬币正面朝上的概率为1,(显然这个结果是未必符合真实情况,因为数据量太少的缘故)。
4. 最大似然估计
极大似然估计,只是一种概率论在统计学的应用,它是参数估计的方法之一。说的是已知某个随机样本满足某种概率分布,但是其中具体的参数不清楚,参数估计就是通过若干次试验,观察其结果,利用结果推出参数的大概值。最大似然估计是建立在这样的思想上:已知某个参数能使这个样本出现的概率最大,我们当然不会再去选择其他小概率的样本,所以干脆就把这个参数作为估计的真实值。
抽取到样本的概率,也就是样本集X中各个样本的联合概率,用下式表示:
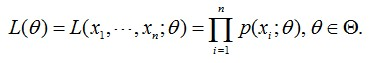
这个概率反映了,在概率密度函数的参数是θ时,得到X这组样本的概率。
因为这里X是已知的,而θ是未知了,则上面这个公式只有θ是未知数,所以它是θ的函数。这个函数放映的是在不同的参数θ取值下,取得当前这个样本集的可能性,因此称为参数θ相对于样本集X的似然函数(likehood function)。记为L(θ)。
有时,可以看到L(θ)是连乘的,所以为了便于分析,还可以定义对数似然函数,将其变成连加的:
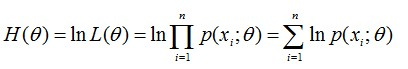
好了,现在我们知道了,要求θ,只需要使θ的似然函数L(θ)极大化,然后极大值对应的θ就是我们的估计。这里就回到了求最值的问题了。怎么求一个函数的最值?当然是求导,然后让导数为0,那么解这个方程得到的θ就是了(当然,前提是函数L(θ)连续可微)。那如果θ是包含多个参数的向量那怎么处理啊?当然是求L(θ)对所有参数的偏导数,也就是梯度了,那么n个未知的参数,就有n个方程,方程组的解就是似然函数的极值点了,当然就得到这n个参数了。
求最大似然函数估计值的一般步骤:
(1)写出似然函数;
(2)对似然函数取对数,并整理;
(3)求导数,令导数为0,得到似然方程;
(4)解似然方程,得到的参数即为所求;
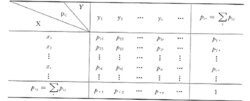
5.如何求解边缘概率分布
:对于二维离散随机向量,设X和Y都是离散型随机变量,{Xi}和 {Yi}分别是X和Y的一切可能的集合,则X和Y的联合概率分布可以表示如下的函数形式和表哥形式:
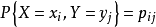





 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 1100
1100

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








