机器学习算法梳理—GBDT算法_gbdt算法公式-优快云博客

本文详细介绍了GBDT算法，从前向分步算法出发，解释了负梯度拟合和损失函数的选择，涵盖了分类问题和回归问题。讨论了正则化的两种方式，步长设置和子采样比例，并分析了GBDT的优缺点，以及在sklearn中的参数设置和应用场景。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

文章目录

本文Boosting家族中另一个重要的算法 梯度提升树(Gradient Boosting Decison Tree, 以下简称GBDT)做一个总结。GBDT有很多简称，有GBT（Gradient Boosting Tree）, GTB（Gradient Tree Boosting ）， GBRT（Gradient Boosting Regression Tree）, MART(Multiple Additive Regression Tree)，其实都是指的同一种算法，本文统一简称GBDT。

一、前向分步算法

在求解加法模型时，公式如下第一个，在给定训练数据及损失函数L(y, f(x))的条件下，学习加法模型f(x)就成为经验风险极小化损失函数极小化问题，公式如下第二个：
在这里插入图片描述

前向分步算法的思想为：学习的是加法模型，那如果能够从前向后，每一步只学习一个基函数及其系数，然后逐步逼近优化目标式（第二式），那么就可以简化优化的复杂度。即每一步优化函数变为：

具体如下：
输入数据：训练数据集T ={(x1,y1), (x2, y2), …, (xN, yN)}；损失函数L(y, f(x))；基函数集{b(x; r)}；
输出：加法模型f(x)
在这里插入图片描述
因此，前向分布算法将同时求解从m=1到M的所有参数βm, rm的优化问题简化为逐次求解各个βm, rm的优化问题。

二、负梯度拟合

在GBDT的迭代中，假设我们前一轮迭代得到的强学习器是 Ht−1(x) , 损失函数是 L(f(x),Ht−1(x)), 我们本轮迭代的目标是找到一个CART回归树模型的弱学习器 ht(x) ，让本轮的损失 L(f(x),ht(x)+Ht−1(x))最小，那么GBDT是如何实现让本轮的损失最小的呢？
　　针对这个问题，大牛Freidman提出了用损失函数的负梯度来拟合本轮损失 L(f(x),ht(x)+Ht−1(x)) 的近似值，进而拟合一个CART回归树。第 t 轮的第 i 个样本的损失函数的负梯度表示为：
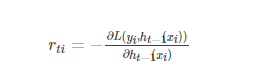
在这里插入图片描述
利用 (xi,rti),i=1