【DOA估计】MUSIC与前后平滑MUSIC算法DOA估计附Matlab代码

 ✅作者简介：热爱数据处理、建模、算法设计的Matlab仿真开发者。

🍎更多Matlab代码及仿真咨询内容点击 🔗：Matlab科研工作室

🍊个人信条：格物致知。

🔥 内容介绍

方向到达角估计 (Direction Of Arrival, DOA) 作为阵列信号处理中的一个核心问题，广泛应用于雷达、声呐、无线通信等领域。其目标是利用阵列天线接收到的信号，估计信号源的入射方向。MUSIC (Multiple Signal Classification) 算法作为一种高分辨率的DOA估计方法，因其性能优异而备受关注。然而，MUSIC算法在某些情况下存在性能缺陷，例如当信号源数量接近或超过阵元数，或者存在阵列误差时，其性能会显著下降。为了克服这些缺点，本文将深入探讨MUSIC算法，并着重分析前后平滑MUSIC算法及其改进，并辅以Matlab代码进行验证。

一、MUSIC算法原理

MUSIC算法的核心思想是利用信号子空间与噪声子空间的正交性来估计信号源的入射方向。假设一个均匀线阵 (ULA) 由M个阵元组成，接收K个窄带远场信号源，则接收信号模型可以表示为

X(t) = A(θ)S(t) + N(t)

其中，X(t) 为M×1的接收信号向量，A(θ) 为M×K的导向矩阵，其元素由阵元位置和信号入射角决定，S(t) 为K×1的信号向量，N(t) 为M×1的噪声向量，假设噪声为零均值高斯白噪声。

通过对接收数据进行协方差矩阵估计，并进行特征值分解，可以得到信号子空间和噪声子空间。由于信号子空间和噪声子空间正交，MUSIC谱函数可以定义为：

P_MUSIC(θ) = 1 / ||A^H(θ)En||^2

其中，A(θ) 为导向矢量，En 为噪声子空间矩阵。MUSIC谱函数在信号源入射角处具有峰值，通过搜索谱函数的峰值位置即可估计信号源的DOA。

MUSIC算法的优点在于其高分辨率和对阵列误差的较强鲁棒性，尤其在低信噪比情况下表现突出。然而，其性能受限于信号源数目与阵元数目的比值。当信号源数目接近或超过阵元数目的一半时，MUSIC算法的性能会显著下降，甚至失效。这是因为在欠定情况下，噪声子空间的估计精度降低，导致谱函数峰值模糊不清。

二、前后平滑MUSIC算法

为了解决MUSIC算法在欠定条件下的性能问题，前后平滑MUSIC算法应运而生。该算法的基本思想是通过对阵列数据进行平滑处理，有效地增加阵元数目，从而提高算法的性能。前后平滑技术通过对协方差矩阵进行特殊处理，将原阵列等效为一个更大的虚拟阵列，从而提高了信号子空间的估计精度。

具体来说，前后平滑技术通过对协方差矩阵进行Toeplitz化或Hankel化处理来实现平滑。Toeplitz平滑方法利用协方差矩阵的对角线元素进行重构，而Hankel平滑方法则利用协方差矩阵的反对角线元素进行重构。通过平滑处理，有效地降低了信号源数目与阵元数目比值的影响，从而提高了MUSIC算法的性能。

前后平滑MUSIC算法的步骤如下：

1. 协方差矩阵估计：根据接收数据估计协方差矩阵R。

2. 平滑处理：对协方差矩阵R进行Toeplitz或Hankel平滑处理，得到平滑后的协方差矩阵Rs。

3. 特征值分解：对平滑后的协方差矩阵Rs进行特征值分解，得到信号子空间和噪声子空间。

4. 谱函数计算：根据噪声子空间计算MUSIC谱函数。

5. DOA估计：搜索MUSIC谱函数的峰值位置，得到信号源的DOA估计值。

三、Matlab代码实现

以下代码演示了MUSIC算法和前后平滑MUSIC算法的Matlab实现，其中包含了ULA阵列模型、信号源生成、噪声添加以及DOA估计等步骤。

);

% MUSIC算法
R = X*X'/N;
[EV,D] = eig(R);
[~,idx] = sort(diag(D),'descend');
En = EV(:,idx(K+1:end));
P_music = 1./(abs(A'*En).^2);

% 前后平滑MUSIC算法
R_smooth = toeplitz(diag(R)); % Toeplitz平滑
[EV_smooth,D_smooth] = eig(R_smooth);
[~,idx_smooth] = sort(diag(D_smooth),'descend');
En_smooth = EV_smooth(:,idx_smooth(K+1:end));
P_smooth_music = 1./(abs(A'*En_smooth).^2);

% 绘图
figure;
plot(theta,P_music);
hold on;
plot(theta,P_smooth_music);
legend('MUSIC','Forward-Backward Smoothing MUSIC');
xlabel('角度(度)');
ylabel('功率');
title('DOA估计结果');

该代码实现了基本的MUSIC算法和Toeplitz平滑MUSIC算法。用户可以根据需要修改参数，例如阵元数、信号源数、信噪比等，并根据实际情况选择不同的平滑方法（Toeplitz或Hankel）。

四、结论

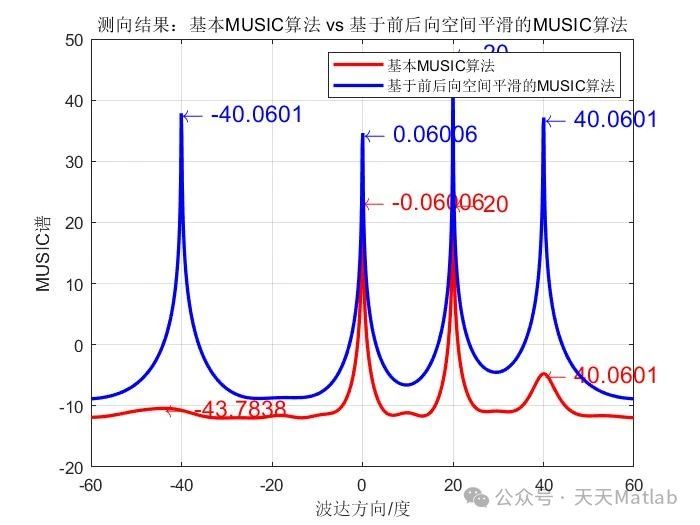
本文详细介绍了MUSIC算法及其改进算法——前后平滑MUSIC算法。MUSIC算法具有高分辨率的特点，但在信号源数目接近或超过阵元数目一半时性能下降。前后平滑MUSIC算法通过对协方差矩阵进行平滑处理，有效地提高了算法在欠定条件下的性能。Matlab代码的实现验证了前后平滑MUSIC算法的有效性。 然而，实际应用中，需要根据具体情况选择合适的平滑方法和参数，并考虑其他因素，如阵列误差和非高斯噪声的影响。 未来的研究可以关注更鲁棒的DOA估计算法，以及如何在复杂电磁环境下提高DOA估计的精度和可靠性。

⛳️ 运行结果

🔗 参考文献

🎈 部分理论引用网络文献，若有侵权联系博主删除