✅作者简介:热爱科研的Matlab仿真开发者,修心和技术同步精进,代码获取、论文复现及科研仿真合作可私信。
🍎个人主页:Matlab科研工作室
🍊个人信条:格物致知。
更多Matlab完整代码及仿真定制内容点击👇
🔥 内容介绍
本文应用机器学习中的人工神经网络(ANN)方法实现相沉积分类过程的自动化。ANN 接收一个数据集,其中包含堪萨斯州休戈顿和帕诺马油田的七口井的数据,包括测井和九种已识别的相沉积数据。这些信息作为输入提供给 ANN,以创建一个模型来预测相沉积类别,模拟实际的相沉积分类研究。首先,使用七口井中的六口井构建模型,使用监督训练过程,而剩余的一口井用作测试井来评估模型性能。随后,更改数据集以均衡不平衡的相沉积类别样本,试图提高模型性能。最后,通过应用样本复杂度研究,探索了数据集大小对网络性能的影响。取得的结果证实,ANN 是相沉积分类中的一个可靠工具,但它也带来了所有机器学习技术的主要缺点,即由于缺乏技术信息,开发的模型极易出错。
引言
相沉积分类是地质学中一项重要的任务,它涉及确定岩石中沉积环境的类型。传统上,相沉积分类是通过对岩芯和测井数据的目视解释来完成的,这既耗时又主观。机器学习技术为自动化相沉积分类过程提供了新的可能性,从而提高了效率和客观性。
人工神经网络(ANN)
ANN 是一种机器学习算法,它模仿人脑中神经元的行为。ANN 由称为神经元的互连层组成,每个神经元接收输入,应用激活函数,并产生输出。通过训练 ANN 来学习从输入数据中提取特征,它可以执行各种任务,包括分类和回归。
数据集
本文使用的数据集包含堪萨斯州休戈顿和帕诺马油田的七口井的数据。数据集包括测井数据(伽马射线、中子孔隙度和声波时差)和九种已识别的相沉积类别。
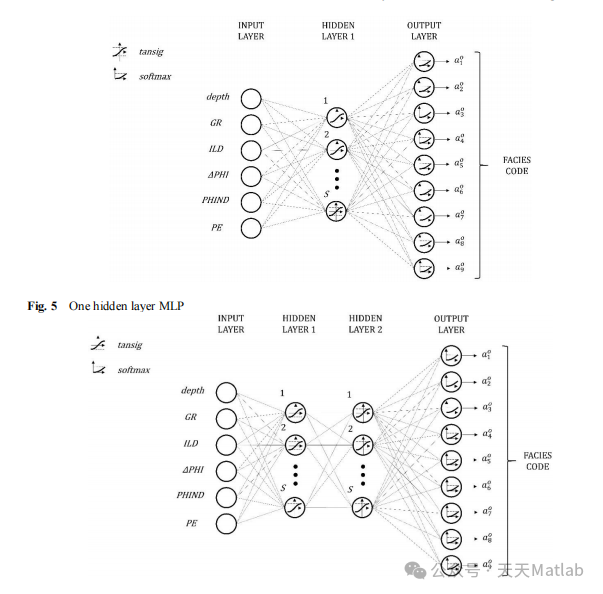
方法
ANN 模型使用监督训练过程构建。六口井的数据用作训练数据,而剩余的一口井用作测试数据。ANN 模型使用反向传播算法进行训练,以最小化训练数据上的损失函数。
为了提高模型性能,数据集被更改为均衡不平衡的相沉积类别样本。还进行了样本复杂度研究,以探索数据集大小对网络性能的影响。
结果
ANN 模型在测试数据上的准确率为 85%。均衡数据集后,准确率提高到 90%。样本复杂度研究表明,随着数据集大小的增加,模型的准确率逐渐提高。
讨论
结果证实,ANN 是相沉积分类中的一个可靠工具。ANN 模型能够从测井数据中学习特征,并准确地预测相沉积类别。均衡数据集和增加数据集大小可以进一步提高模型性能。
然而,ANN 模型也存在一些缺点。由于缺乏技术信息,开发的模型极易出错。此外,ANN 模型是黑箱模型,难以解释其决策过程。
结论
ANN 是自动化相沉积分类过程的有前途的技术。ANN 模型能够从测井数据中学习特征,并准确地预测相沉积类别。然而,ANN 模型也存在一些缺点,需要进一步的研究来解决这些缺点。
📣 部分代码
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% COMPLETE BRUTE FORCE CODE%DATA_DIVIDED_NOF9_NOFEATURES.mat is needed%% set global variablesglobal AccuracyM1_tot; global AccuracyM1_test; global AccuracyM2_tot; global AccuracyM2_test; global AccuracyM3_test; global AccuracyM3_tot;global F1M1avg; global F1M2avg; global F1M3avg;global Ystore; global YINDstore; global ETest;global STOREy; global STOREtr;global F1M1avg_tot; global F1M2avg_tot; global F1M3avg_tot;%resetAccuracyM1_tot ={}; AccuracyM1_test={}; AccuracyM2_tot={}; AccuracyM2_test={}; AccuracyM3_test={}; AccuracyM3_tot={};F1M1avg={}; F1M2avg={}; F1M3avg={};Ystore={}; YINDstore={}; ETest = [];STOREy={}; STOREtr={};F1M1avg_tot={}; F1M2avg_tot={}; F1M3avg_tot={};%% SET UP INPUT AND TARGET AND RESET ARRAYx = input_data;t = target_data;%defining rangesrangeHidden = [1,2,4,8,16,32,64,128]; %NUMBEER OF NEURONS FOR EACH LAYERrangeLayers = 2:3; % 2 or 3 hidden layersrangeVote = 1:10; %only 2 votes%figuresF1=figure; F12=figure; Accuracy1=figure; Accuracy2=figure; RoCurve1=figure; RoCurve2=figure;%% START LOOPfor w = 1:length(WELLS_data)for layers = rangeLayersfor hidden = rangeHiddenfor vote = rangeVote[net] = ArchitectureSetUp(layers,hidden,x,t);[net] = DivideindNOVaL(net,w,x,t,WELLS_data);% [net] = Divideind(net,w,x,t,WELLS_data);[net] = TrainingFunctionSetUp(net);[net,tr] = train(net,x,t); %training[Ystore,YINDstore,y,tind,yind,ETest] = Test(net,x,t,Ystore,YINDstore,vote,tr,ETest); %testend%voting results[y,yind,STOREy,STOREtr,Ystore,YINDstore] = Vote(Ystore,YINDstore,tind,STOREy,STOREtr,tr,w,layers,hidden);% [y,yind,STOREy,STOREtr,Ystore,YINDstore,ETest] = VoteTheBest(ETest,Ystore,YINDstore,STOREy,STOREtr,tr,w,layers,hidden);% Calculate Accuracy and F1[AccuracyM1_test,AccuracyM1_tot] = Accuracy_M1(AccuracyM1_test,AccuracyM1_tot,tind,yind,hidden,tr,w,layers);[AccuracyM2_test,AccuracyM2_tot] = Accuracy_M2(AccuracyM2_test,AccuracyM2_tot,tind,yind,hidden,tr,w,layers);[AccuracyM3_test,AccuracyM3_tot] = Accuracy_M3(AccuracyM3_test,AccuracyM3_tot,tind,yind,hidden,tr,w,layers);[F1M1avg,F1M1,precision_M1,recall_M1] = F1_M1(F1M1avg,facies,w,tr,yind,tind,layers,hidden);[F1M2avg,F1M2,precision_M2,recall_M2] = F1_M2(F1M2avg,facies,w,tr,yind,tind,layers,hidden);[F1M3avg,precision_M3,recall_M3] = F1_M3(F1M3avg,w,tr,yind,tind,layers,hidden);[F1M1avg_tot,F1M1_tot,precision_M1_tot,recall_M1_tot] = F1_M1_tot(F1M1avg_tot,facies,w,tr,yind,tind,layers,hidden);[F1M2avg_tot,F1M2_tot,precision_M2_tot,recall_M2_tot] = F1_M2_tot(F1M2avg_tot,facies,w,tr,yind,tind,layers,hidden);[F1M3avg_tot,precision_M3_tot,recall_M3_tot] = F1_M3_tot(F1M3avg_tot,w,tr,yind,tind,layers,hidden);endROC(RoCurve1,RoCurve2,w,t,tr,y,layers); %needs to be here cause tr is calculated and overwrittenPlotting(rangeHidden,w,layers,F1M1avg,F1M2avg,F1M3avg,AccuracyM1_test,AccuracyM2_test,AccuracyM3_test,F1,F12,Accuracy1,Accuracy2);endend%find best architectureBests(rangeHidden,rangeLayers,F1M1avg,F1M2avg,F1M3avg,AccuracyM1_test,AccuracyM2_test,AccuracyM3_test)save FINAL_128_10tries_AVGvote.mat%% FUNCTIONSfunction [net] = ArchitectureSetUp(layers,hidden,x,t)numInputs = 1; numLayers = layers;biasConnect = ones(layers,1); inputConnect = [1 ;zeros(layers-1,1)]; outputConnect = [zeros(1,layers-1) 1];layerConnect = zeros(layers);for i = 2:layerslayerConnect(i,i-1) = 1;endnet = network(numInputs,numLayers,biasConnect,inputConnect,layerConnect,outputConnect);%start to configure the networknet = configure(net,x,t);%set up the layers namefor i = 1:layersif i == 1net.layers{i,1}.name = 'input layer';elseif i == layersnet.layers{i,1}.name = 'output layer';elsenet.layers{i,1}.name = "hidden layer" + i ;endend%set up the layer dimensionsfor i = 1:layersif i == layersnet.layers{i,1}.dimensions = 9;elsenet.layers{i,1}.dimensions = hidden;endend%set up the layer transfer functionfor i = 1:layersif i == layersnet.layers{i,1}.transferFcn = "softmax";elsenet.layers{i,1}.transferFcn = "tansig";endend%set up the net input function and %set up the W and b initialization function algorithmfor i = 1:layersnet.layers{i,1}.netInputFcn = "netsum";net.layers{i,1}.initFcn= "initnw";end% SET UP DATA PRE-PROCESSING FUNCTIONSnet.input.processFcns = {'removeconstantrows','mapminmax'};% set up performance functionnet.performFcn = 'crossentropy'; % Cross-Entropyendfunction [net] = DivideindNOVaL(net,w,x,t,WELLS_data)%% ORDER DATAtraining_data = [];training_index = [];training_find = [];for i = 1:length(WELLS_data)if i == wtraining_index = [training_index zeros(1,length(WELLS_data{2,i}))];continueendtraining_data =[training_data x(:,WELLS_data{2,i})];training_index = [training_index ones(1,length(WELLS_data{2,i}))];training_find = find(training_index);endtest_well_data = x(:,WELLS_data{2,w});test_well_index = training_index <1;test_well_find = find (test_well_index);%test well indextestIndex = test_well_index;%train wells indicestrainIndex = testIndex <1 ;%%net.divideFcn = 'divideind'; % Divide up for indexnet.divideMode = 'sample'; % Divide up every sample[trainInd,testInd]=divideind(length(t),find(trainIndex), find(testIndex));net.divideParam.trainInd=trainInd;net.divideParam.testInd=testInd;endfunction [net] = Divideind(net,w,x,t,WELLS_data)%% ORDER DATAtraining_data = [];training_index = [];training_find = [];for i = 1:length(WELLS_data)if i == wtraining_index = [training_index zeros(1,length(WELLS_data{2,i}))];continueendtraining_data =[training_data x(:,WELLS_data{2,i})];training_index = [training_index ones(1,length(WELLS_data{2,i}))];training_find = find(training_index);end
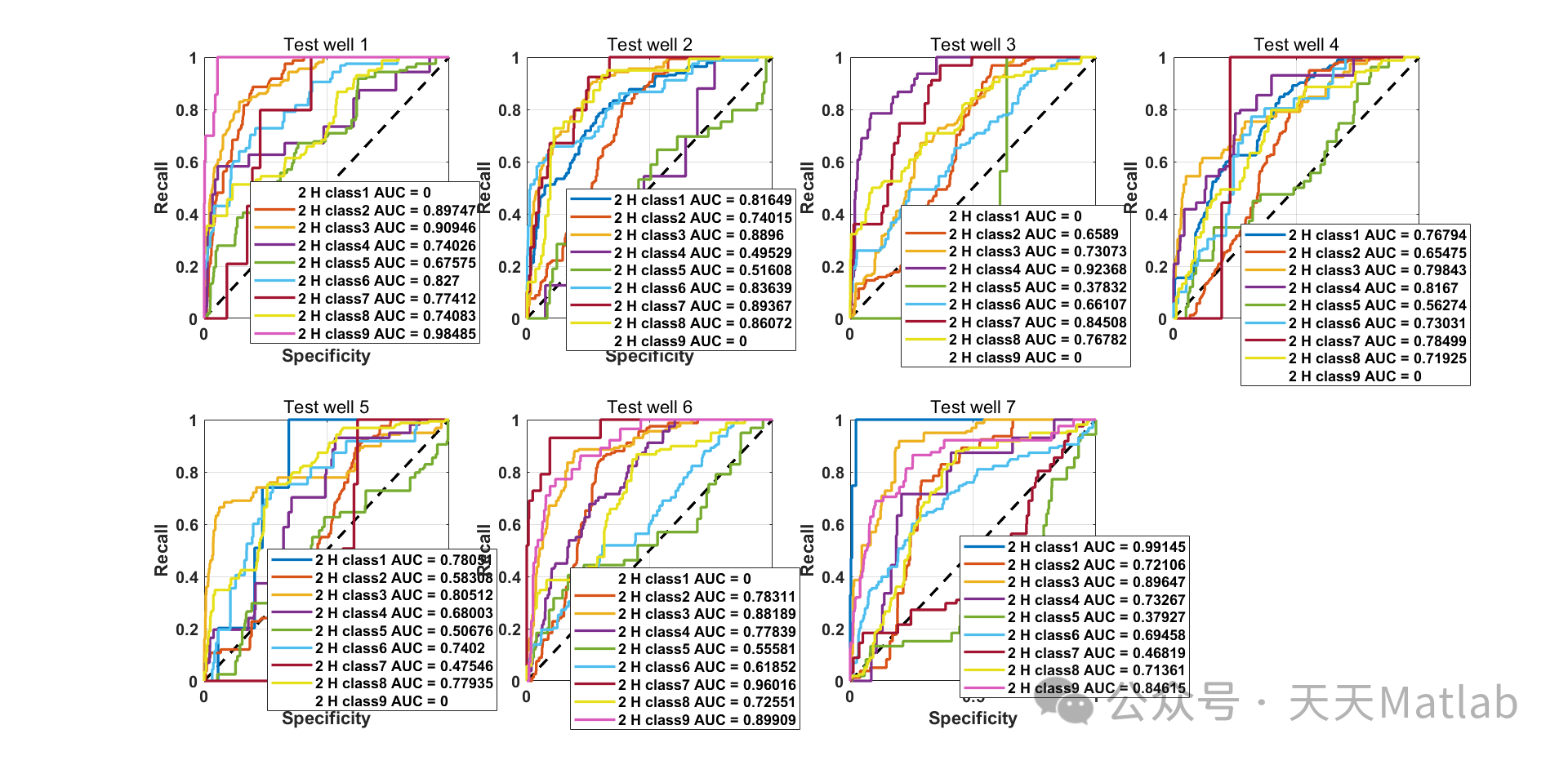
⛳️ 运行结果
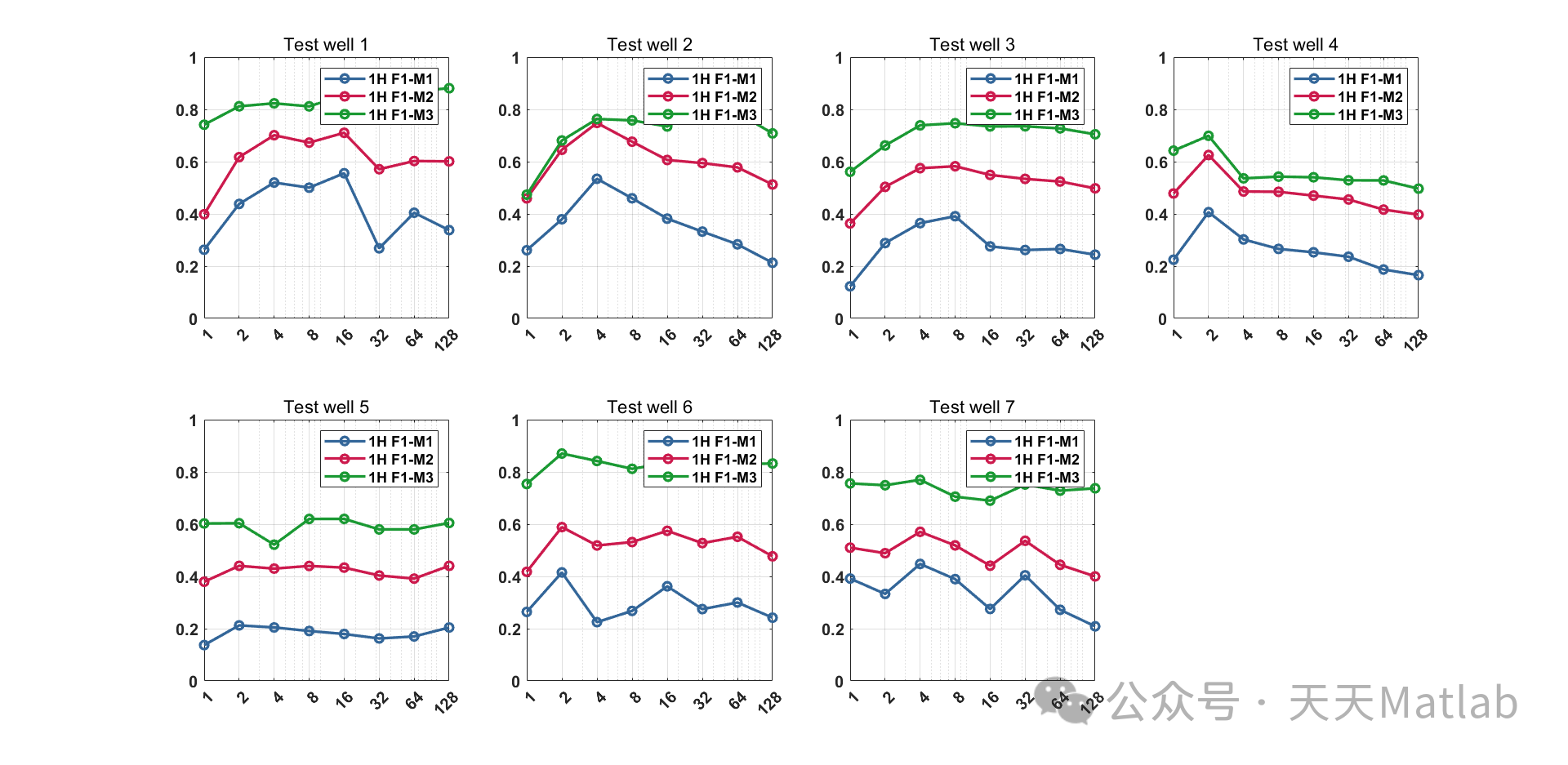
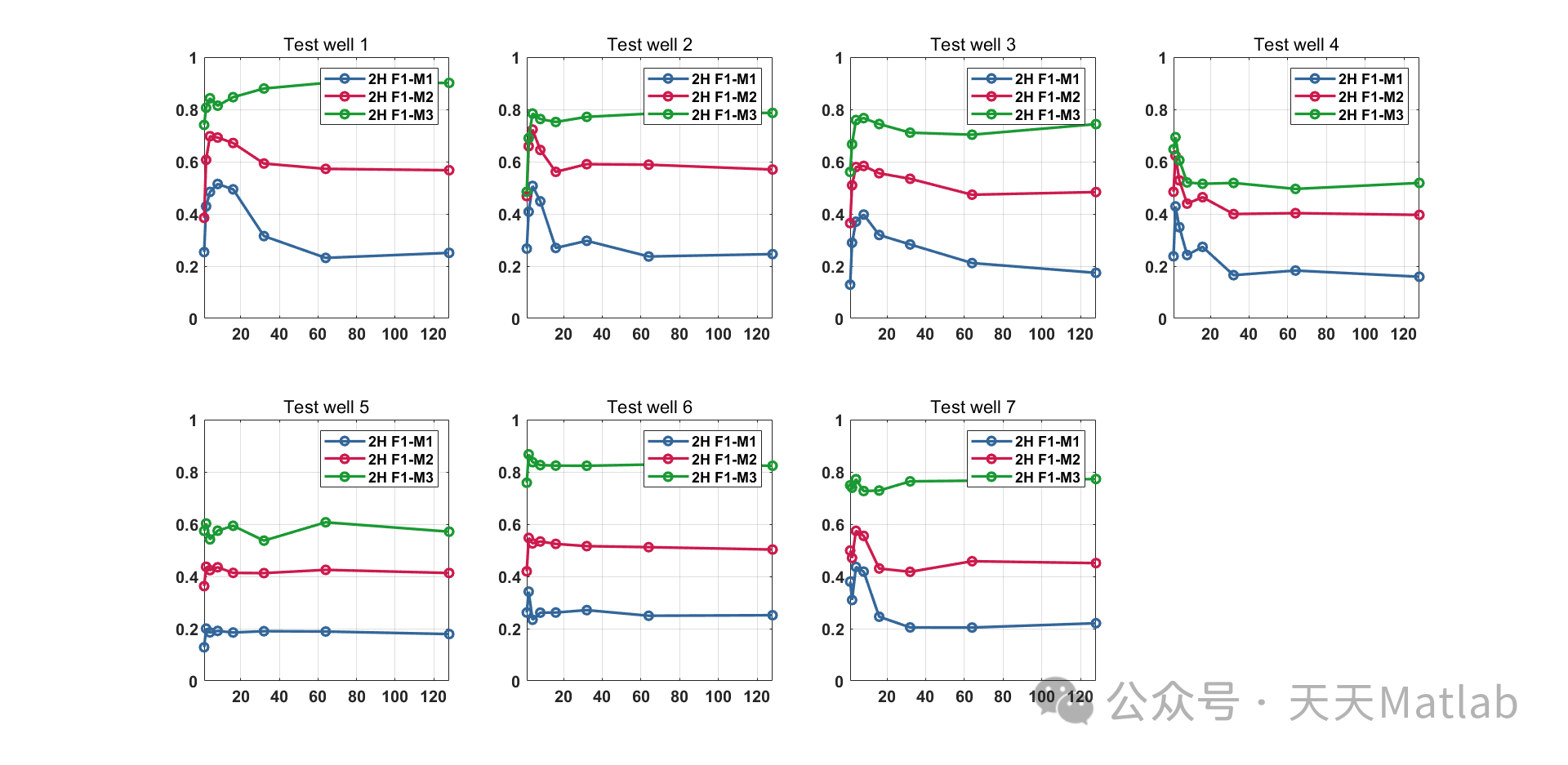
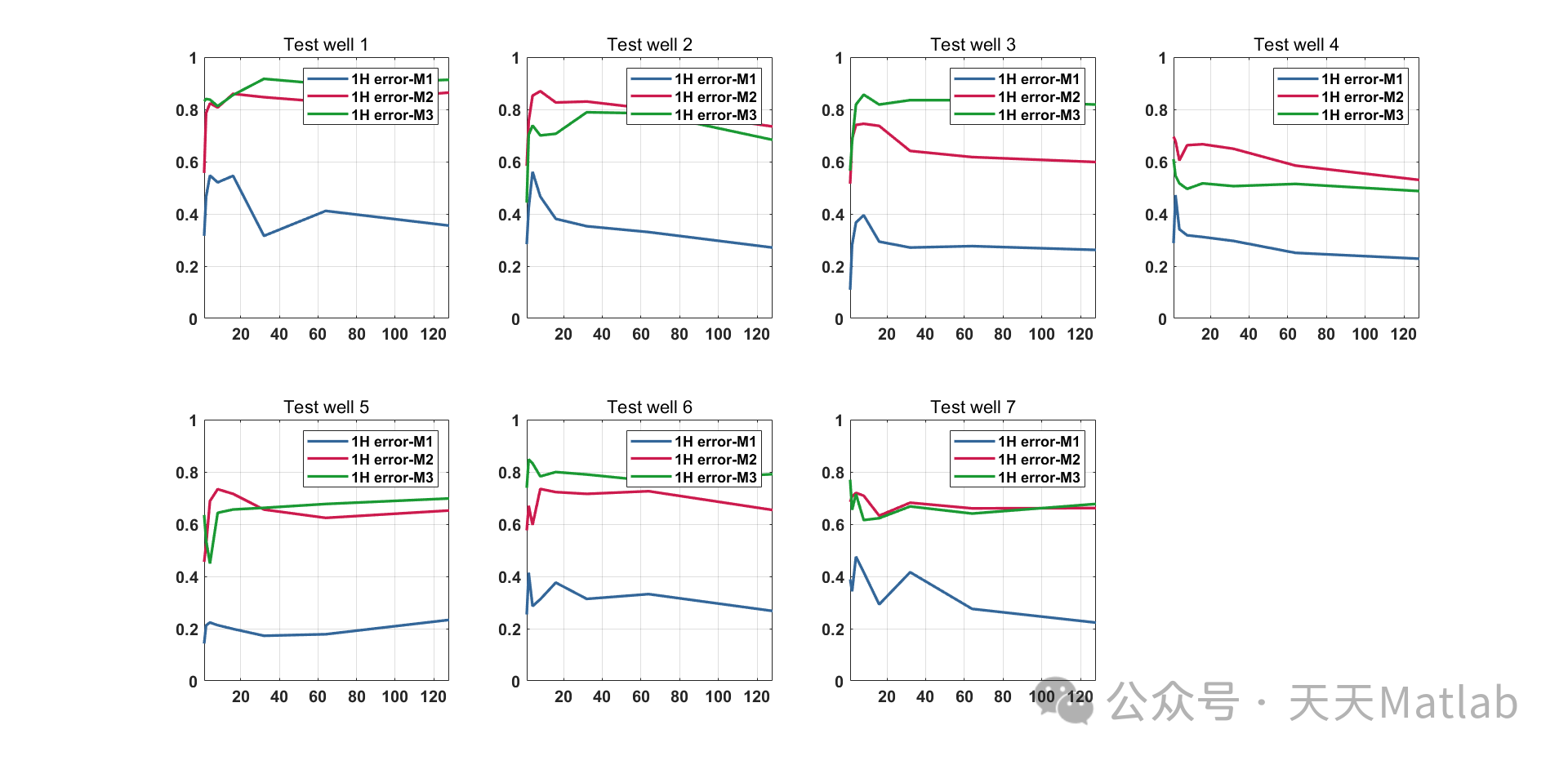
🔗 参考文献
🎈 部分理论引用网络文献,若有侵权联系博主删除
🎁 关注我领取海量matlab电子书和数学建模资料
👇 私信完整代码和数据获取及论文数模仿真定制
1 各类智能优化算法改进及应用
生产调度、经济调度、装配线调度、充电优化、车间调度、发车优化、水库调度、三维装箱、物流选址、货位优化、公交排班优化、充电桩布局优化、车间布局优化、集装箱船配载优化、水泵组合优化、解医疗资源分配优化、设施布局优化、可视域基站和无人机选址优化、背包问题、 风电场布局、时隙分配优化、 最佳分布式发电单元分配、多阶段管道维修、 工厂-中心-需求点三级选址问题、 应急生活物质配送中心选址、 基站选址、 道路灯柱布置、 枢纽节点部署、 输电线路台风监测装置、 集装箱船配载优化、 机组优化、 投资优化组合、云服务器组合优化、 天线线性阵列分布优化
2 机器学习和深度学习方面
2.1 bp时序、回归预测和分类
2.2 ENS声神经网络时序、回归预测和分类
2.3 SVM/CNN-SVM/LSSVM/RVM支持向量机系列时序、回归预测和分类
2.4 CNN/TCN卷积神经网络系列时序、回归预测和分类
2.5 ELM/KELM/RELM/DELM极限学习机系列时序、回归预测和分类
2.6 GRU/Bi-GRU/CNN-GRU/CNN-BiGRU门控神经网络时序、回归预测和分类
2.7 ELMAN递归神经网络时序、回归\预测和分类
2.8 LSTM/BiLSTM/CNN-LSTM/CNN-BiLSTM/长短记忆神经网络系列时序、回归预测和分类
2.9 RBF径向基神经网络时序、回归预测和分类





 本文介绍了如何使用机器学习中的人工神经网络(ANN)对堪萨斯州休戈顿和帕诺马油田的测井数据进行相沉积分类,通过监督训练和样本均衡策略提升模型性能,结果显示ANN在相沉积分类中表现出高可靠性,但也强调了模型对技术信息依赖的问题。
本文介绍了如何使用机器学习中的人工神经网络(ANN)对堪萨斯州休戈顿和帕诺马油田的测井数据进行相沉积分类,通过监督训练和样本均衡策略提升模型性能,结果显示ANN在相沉积分类中表现出高可靠性,但也强调了模型对技术信息依赖的问题。

















 101
101

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










