✅作者简介:热爱科研的Matlab仿真开发者,修心和技术同步精进,matlab项目合作可私信。
🍎个人主页:Matlab科研工作室
🍊个人信条:格物致知。
更多Matlab完整代码及仿真定制内容点击👇
🔥 内容介绍
在过去的几十年中,卡尔曼滤波器一直被广泛应用于状态估计问题。然而,随着深度学习的兴起,研究人员开始探索将传统的卡尔曼滤波器与神经网络相结合的方法,以提高状态估计的准确性和鲁棒性。最近,一种将Transformer和LSTM与EM算法结合到卡尔曼滤波器中的方法引起了广泛关注。
Transformer是一种基于自注意力机制的神经网络模型,最初用于自然语言处理任务。它通过对输入序列中的每个元素进行自注意力计算,从而捕捉序列中元素之间的依赖关系。与传统的循环神经网络(如LSTM)相比,Transformer具有并行计算的优势,并且在处理长序列时表现更好。
LSTM是一种经典的循环神经网络模型,被广泛应用于序列建模和预测任务。它通过使用门控单元来捕捉序列中的长期依赖关系,从而在处理时间序列数据时表现出色。然而,LSTM在处理长序列时存在计算效率低下的问题。
EM算法(Expectation-Maximization algorithm)是一种迭代优化算法,常用于解决含有隐变量的概率模型的参数估计问题。它通过交替进行E步骤和M步骤来最大化似然函数,从而逐步优化模型参数。EM算法在状态估计问题中具有广泛的应用,特别是在卡尔曼滤波器中。
将Transformer和LSTM与EM算法结合到卡尔曼滤波器中的方法主要包括以下几个步骤:
-
使用Transformer或LSTM模型对输入序列进行建模。这些模型将序列中的每个元素作为输入,并通过自注意力或门控单元来捕捉元素之间的依赖关系。
-
使用EM算法进行参数估计。在每次迭代中,通过E步骤计算隐变量的期望,并通过M步骤更新模型参数。这样,模型可以逐步优化,以更好地拟合观测数据。
-
将卡尔曼滤波器应用于状态估计。通过将Transformer或LSTM模型的输出与卡尔曼滤波器的观测模型相结合,可以得到更准确的状态估计结果。
将Transformer和LSTM与EM算法结合到卡尔曼滤波器中的方法具有许多优势。首先,通过使用深度学习模型,可以更好地捕捉序列中的依赖关系,从而提高状态估计的准确性。其次,EM算法能够通过迭代优化模型参数,进一步提高状态估计的性能。最后,与传统的卡尔曼滤波器相比,这种方法可以处理更长的序列,并具有更好的计算效率。
然而,将Transformer和LSTM与EM算法结合到卡尔曼滤波器中也存在一些挑战。首先,模型的参数估计可能会受到局部最优解的影响,需要进行合适的正则化和初始化。其次,模型的训练和推理过程可能会比传统的卡尔曼滤波器复杂,需要更多的计算资源和时间。
总之,将Transformer和LSTM与EM算法结合到卡尔曼滤波器中是一种有潜力的方法,可以提高状态估计的准确性和鲁棒性。未来的研究可以进一步探索这种方法的应用范围,并解决其中的挑战。这将有助于推动状态估计领域的发展,并在实际应用中取得更好的效果。
📣 部分代码
function [F,Pre,Recall,TP,FP,FN,numo]=cell_measures(I,G)% if max(max(I))>0TP=0;FP=0;FN=0;[xg,yg]=size(G);G(1,:)=0;G(xg,:)=0;G(:,1)=0;G(:,yg)=0;G=bwareaopen(G,15,4);I=bwareaopen(I,15,4);[L1,~]=bwlabel(I,4);S=regionprops(L1,'Centroid');Centroids=cat(1,S.Centroid);[numfp,~]=size(Centroids);xs=Centroids(:,1);ys=Centroids(:,2);[L,num]=bwlabel(G,8);numo=num;R1=logical(zeros(size(G)));for i=1:numR=logical(zeros(size(G)));R(find(L==i))=1;% figure,imshow(R),hold on,plot(xs,ys,'r.','MarkerSize',25);bwg=bwboundaries(R,4,'noholes');[in,on]=inpolygon(xs,ys,bwg{1}(:,2),bwg{1}(:,1));if numel(xs(in))>1 %TP=TP+1;FP=FP+numel(xs(in))-1;numfp=numfp-numel(xs(in))-1;elseif numel(xs(in))==1 %TP=TP+1;numfp=numfp-1;endif numel(xs(on))>0 %FP=FP+numel(xs(on));numfp=numfp-numel(xs(on));endif numel(xs(in))==0FN=FN+1;endendFP=FP+numfp;Pre=TP/(TP+FP);Recall=TP/(TP+FN);F=Pre*Recall*2/(Pre+Recall);% end
⛳️ 运行结果
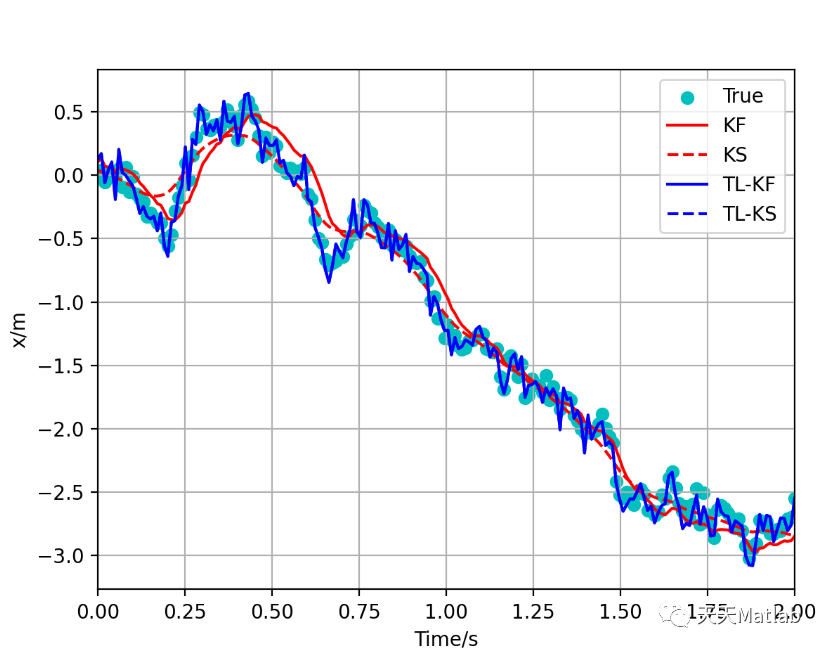
🔗 参考文献
[1] 向礼,柳明,苏宝库.高斯混合粒子滤波器在静基座捷联惯导系统初始对准中的应用[J].大连海事大学学报, 2008, 34(2):5.DOI:CNKI:SUN:DLHS.0.2008-02-015.
[2] 郭映维.基于复数型扩展卡尔曼滤波器状态估计的感应电机直接转矩控制研究[J]. 2015.





 本文探讨了深度学习如何通过结合Transformer和LSTM模型与EM算法改进卡尔曼滤波器,以提升状态估计的精度和鲁棒性。方法利用Transformer的自注意力机制和LSTM的长期依赖捕捉能力,配合EM算法优化参数,适用于处理长序列和复杂依赖。虽然存在挑战,但这种方法展示了巨大潜力,未来有望推动状态估计技术的发展。
本文探讨了深度学习如何通过结合Transformer和LSTM模型与EM算法改进卡尔曼滤波器,以提升状态估计的精度和鲁棒性。方法利用Transformer的自注意力机制和LSTM的长期依赖捕捉能力,配合EM算法优化参数,适用于处理长序列和复杂依赖。虽然存在挑战,但这种方法展示了巨大潜力,未来有望推动状态估计技术的发展。

















 919
919

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










