✅作者简介:热爱科研的Matlab仿真开发者,修心和技术同步精进,matlab项目合作可私信。
🍎个人主页:Matlab科研工作室
🍊个人信条:格物致知。
更多Matlab仿真内容点击👇
⛄ 内容介绍
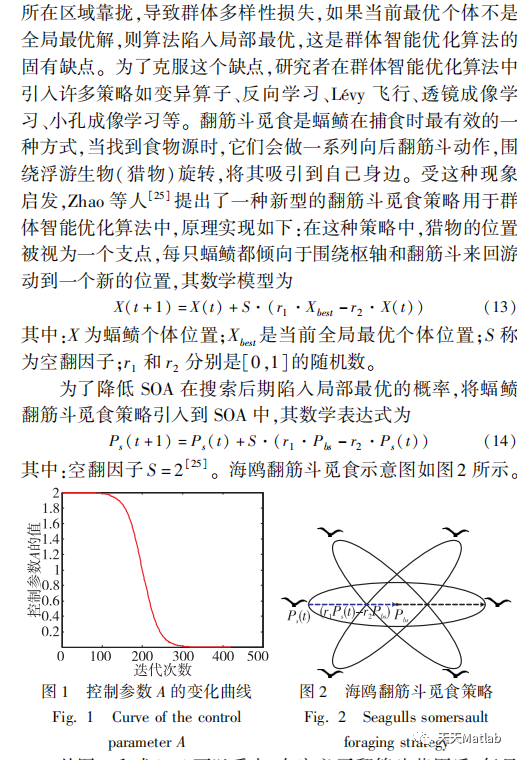
针对基本海鸥优化算法(SOA)在处理复杂优化问题中存在低精度,慢收敛和易陷入局部最优的不足,提出了一种基于翻筋斗觅食策略的SOA算法(SFSOA).该算法首先采用基于倒S型函数的控制参数A非线性递减策略更新海鸥个体的位置,以改善个体的质量和加快收敛速度;引入一种基于翻筋斗觅食策略的学习机制以增加海鸥个体位置的多样性,避免算法在搜索后期陷入局部最优值.选取八个基准函数优化问题进行数值实验,并与基本SOA,灰狼优化算法和改进SOA进行比较,结果表明,所提算法具有较高的解精度,较快的收敛速度和较强的全局搜索能力,能有效地处理复杂函数优化问题.
SFSOA(基于翻筋斗觅食海鸥优化算法)是一种基于海鸥觅食行为的优化算法。该算法的灵感来源于海鸥在觅食过程中的,海鸥行为通过观察周围的环境,执行一系列的翻滚和盘旋动作来寻找食物。
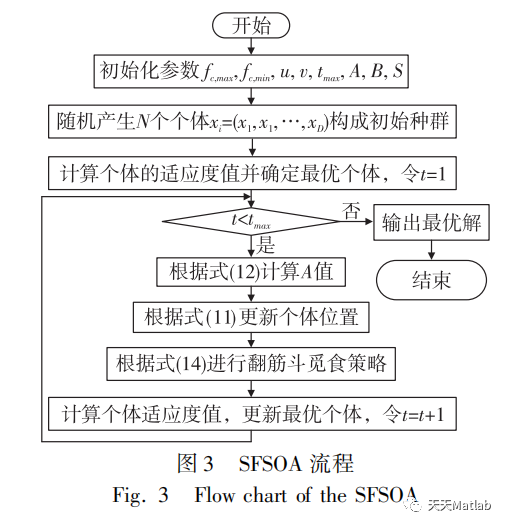
SFSOA算法的主要步骤包括初始化操作重置、计算适应度、选择、翻滚和盘旋、更新位置和适应度、以及终止条件判断等。具体来说,算法通过将问题的解表示为海鸥的位置,并利用翻滚和盘旋操作来搜索最优解。
在翻滚操作中,海鸥会以一定的角度和速度进行滚动动作,促进更深入的地面搜索环境。而在盘旋操作中,海鸥会一定以一定的半径和速度进行盘旋动作,促进更深入的地面搜索。不断地迭代执行这些操作,SFSOA算法能够逐步优化解空间,以寻找更好的解。
SFSOA算法具有更好的全局搜索能力和快速收敛性


⛄ 部分代码
%%% Designed and Developed by Dr. Gaurav Dhiman () %%%function[Score,Position,Convergence]=SOA(Search_Agents,Max_iterations,Lower_bound,Upper_bound,dimension,objective)Position=zeros(1,dimension);Score=inf;Positions=init(Search_Agents,dimension,Upper_bound,Lower_bound);Convergence=zeros(1,Max_iterations);l=0;while l<Max_iterationsfor i=1:size(Positions,1)Flag4Upper_bound=Positions(i,:)>Upper_bound;Flag4Lower_bound=Positions(i,:)<Lower_bound;Positions(i,:)=(Positions(i,:).*(~(Flag4Upper_bound+Flag4Lower_bound)))+Upper_bound.*Flag4Upper_bound+Lower_bound.*Flag4Lower_bound;fitness=objective(Positions(i,:));if fitness<ScoreScore=fitness;Position=Positions(i,:);endendFc=2-l*((2)/Max_iterations);for i=1:size(Positions,1)for j=1:size(Positions,2)r1=rand();r2=rand();A1=2*Fc*r1-Fc;C1=2*r2;b=1;ll=(Fc-1)*rand()+1;D_alphs=Fc*Positions(i,j)+A1*((Position(j)-Positions(i,j)));X1=D_alphs*exp(b.*ll).*cos(ll.*2*pi)+Position(j);Positions(i,j)=X1;endendl=l+1;Convergence(l)=Score;end
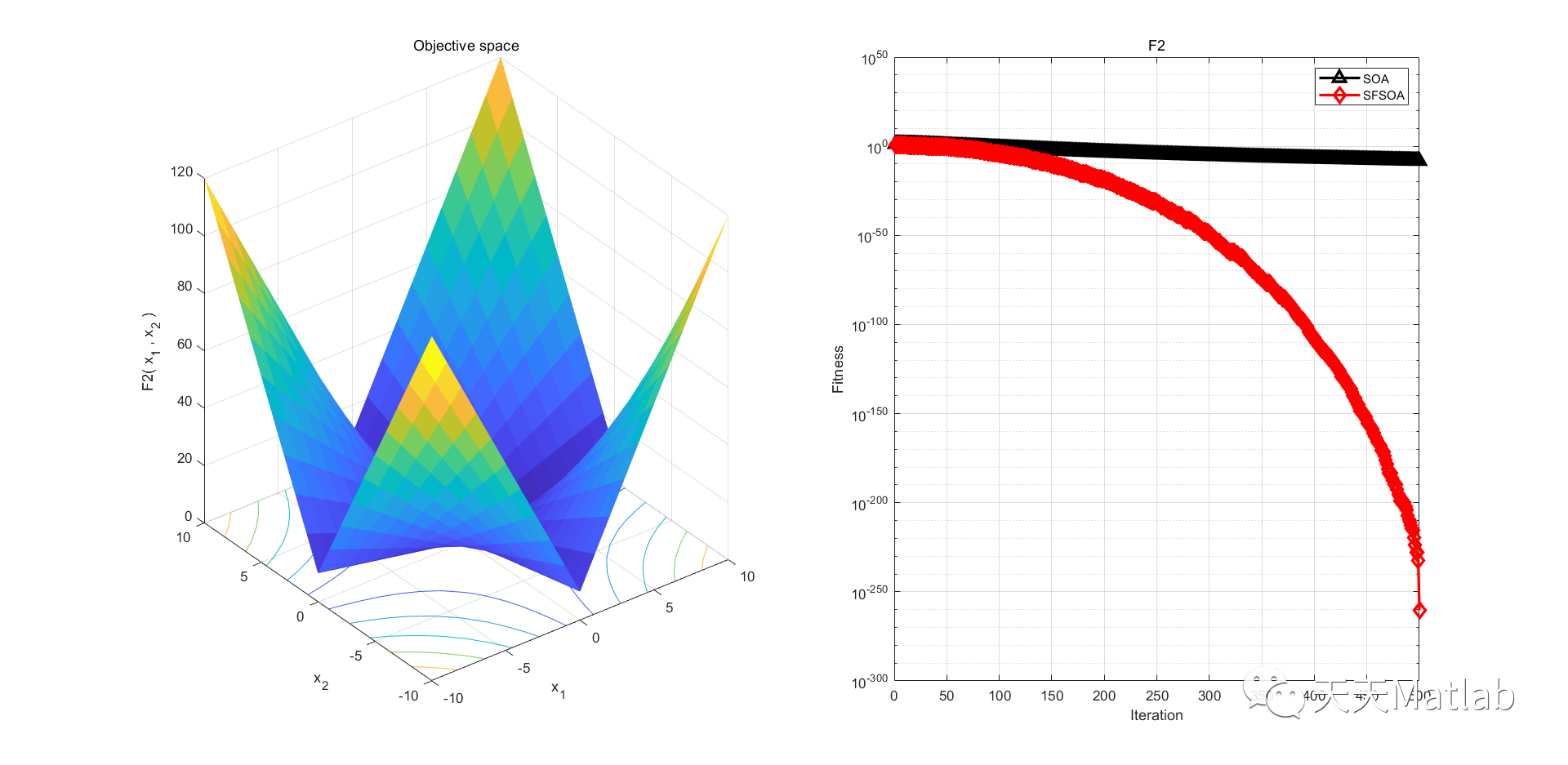
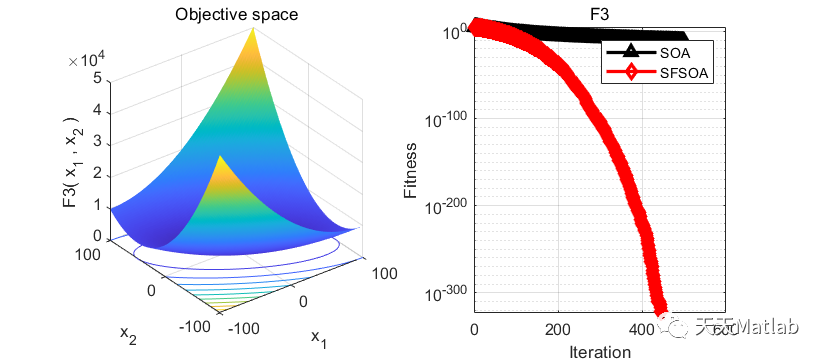
⛄ 运行结果
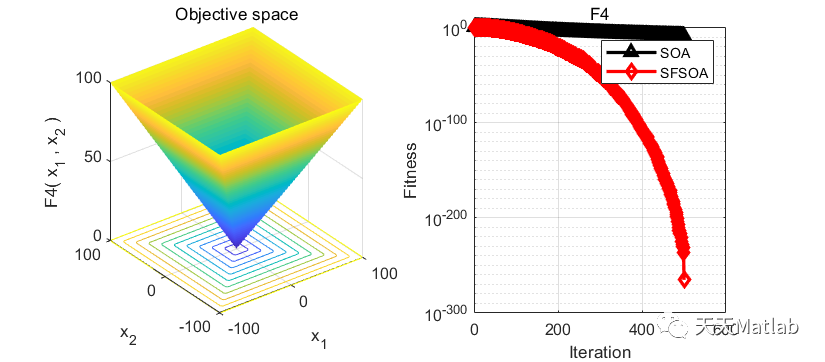
⛄ 参考文献
[1]徐明龙文羊洋.用于函数优化和特征选择的翻筋斗觅食海鸥优化算法[J].计算机应用研究, 2022, 39(12):3639-3643.





 文章提出了一种基于翻筋斗觅食策略的海鸥优化算法(SFSOA),旨在解决基本海鸥优化算法在处理复杂问题时的低精度和慢收敛问题。SFSOA通过倒S型函数控制参数和翻筋斗觅食学习机制增强搜索性能,经数值实验验证,显示了更高的解精度、更快的收敛速度和更强的全局搜索能力,适用于复杂函数优化。
文章提出了一种基于翻筋斗觅食策略的海鸥优化算法(SFSOA),旨在解决基本海鸥优化算法在处理复杂问题时的低精度和慢收敛问题。SFSOA通过倒S型函数控制参数和翻筋斗觅食学习机制增强搜索性能,经数值实验验证,显示了更高的解精度、更快的收敛速度和更强的全局搜索能力,适用于复杂函数优化。

















 82
82

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










