【智能优化算法】基于改进鲸鱼算法HIWOA求解单目标优化问题附matlab代码

✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，matlab项目合作可私信。

 

🍎个人主页：Matlab科研工作室

🍊个人信条：格物致知。

更多Matlab仿真内容点击👇

智能优化算法       神经网络预测       雷达通信       无线传感器        电力系统

信号处理              图像处理               路径规划       元胞自动机        无人机 

⛄ 内容介绍

Aiming at the problems that whale optimization algorithm is easy to fall into local optimal, slow convergence speed and low accuracy in the complex environment of multi-variable processing, it has always been challenging in practical application. In this paper, a new hybrid modified whale optimization algorithm (HIWOA) is proposed, which adds a new feedback mechanism to improve population diversity and reduce the possibility of falling into local optimization. The nonlinear convergence factor and inertia weight coefficient are used to improve the updating of whale individual position and improve the speed of convergence and accuracy. Simulation experiments were carried out on 23 benchmark functions, and the results showed that compared with the original WOA algorithm and the other three improved algorithms in the last two years, the HIWOA algorithm was more competitive in accuracy of solution, convergence speed and stability.

⛄ 部分代码

%_________________________________________________________________________%

% 鲸鱼优化算法             %

%_________________________________________________________________________%

% The Whale Optimization Algorithm

function [Leader_score,Leader_pos,Convergence_curve]=WOA(SearchAgents_no,Max_iter,lb,ub,dim,fobj)

% initialize position vector and score for the leader 

Leader_pos=zeros(1,dim);

Leader_score=inf; %change this to -inf for maximization problems

%Initialize the positions of search agents

Positions=initialization(SearchAgents_no,dim,ub,lb);

Convergence_curve=zeros(1,Max_iter);

t=0;% Loop counter

% Main loop

while t<Max_iter

    for i=1:size(Positions,1)

        

        % Return back the search agents that go beyond the boundaries of the search space

        Flag4ub=Positions(i,:)>ub;

        Flag4lb=Positions(i,:)<lb;

        Positions(i,:)=(Positions(i,:).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;

        

        % Calculate objective function for each search agent

        fitness=fobj(Positions(i,:));

        

        % Update the leader

        if fitness<Leader_score % Change this to > for maximization problem

            Leader_score=fitness; % Update alpha

            Leader_pos=Positions(i,:);

        end

        

    end

    

    a=2-t*((2)/Max_iter); % a decreases linearly fron 2 to 0 in Eq. (2.3)

    

    % a2 linearly dicreases from -1 to -2 to calculate t in Eq. (3.12)

    a2=-1+t*((-1)/Max_iter);

    

    % Update the Position of search agents 

    for i=1:size(Positions,1)

        r1=rand(); % r1 is a random number in [0,1]

        r2=rand(); % r2 is a random number in [0,1]

        

        A=2*a*r1-a;  % Eq. (2.3) in the paper

        C=2*r2;      % Eq. (2.4) in the paper

        

        

        b=1;               %  parameters in Eq. (2.5)

        l=(a2-1)*rand+1;   %  parameters in Eq. (2.5)

        

        p = rand();        % p in Eq. (2.6)

        

        for j=1:size(Positions,2)

            

            if p<0.5   

                if abs(A)>=1

                    rand_leader_index = floor(SearchAgents_no*rand()+1);

                    X_rand = Positions(rand_leader_index, :);

                    D_X_rand=abs(C*X_rand(j)-Positions(i,j)); % Eq. (2.7)

                    Positions(i,j)=X_rand(j)-A*D_X_rand;      % Eq. (2.8)

                    

                elseif abs(A)<1

                    D_Leader=abs(C*Leader_pos(j)-Positions(i,j)); % Eq. (2.1)

                    Positions(i,j)=Leader_pos(j)-A*D_Leader;      % Eq. (2.2)

                end

                

            elseif p>=0.5

              

                distance2Leader=abs(Leader_pos(j)-Positions(i,j));

                % Eq. (2.5)

                Positions(i,j)=distance2Leader*exp(b.*l).*cos(l.*2*pi)+Leader_pos(j);

                

            end

            

        end

    end

    t=t+1;

    Convergence_curve(t)=Leader_score;

end

⛄ 运行结果

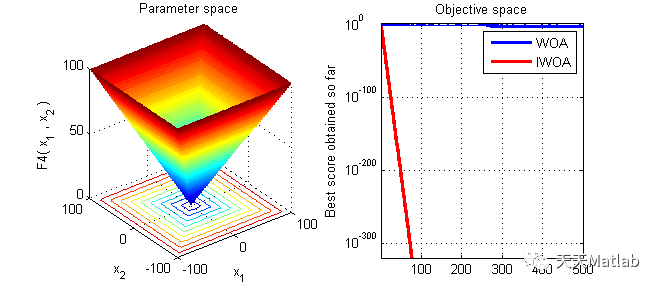
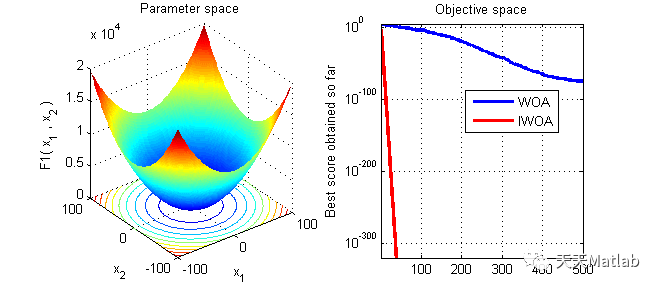
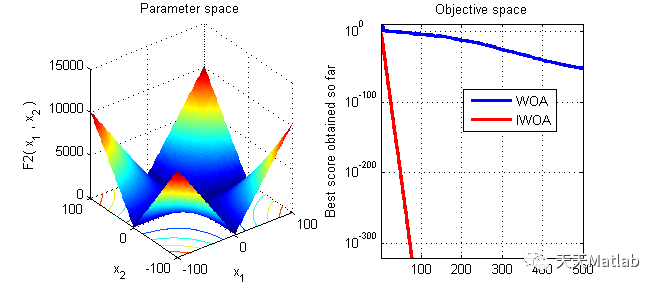
⛄ 参考文献

[1] Tang C ,  Sun W ,  Wu W , et al. A hybrid improved whale optimization algorithm[C]// 2019 IEEE 15th International Conference on Control and Automation (ICCA). IEEE, 2019.

⛳️ 代码获取关注我

❤️部分理论引用网络文献，若有侵权联系博主删除

❤️ 关注我领取海量matlab电子书和数学建模资料