【智能优化算法】一种改进的灰狼算法附matlab代码

 1 简介

Grey wolf optimization (GWO) algorithm is a new emerging algorithm that is based on the social hierarchy of grey wolves as well as their hunting and cooperation strategies. Introduced in 2014, this algorithm has been used by a large number of researchers and designers, such that the number of citations to the original paper exceeded many other algorithms. In a recent study by Niu et al., one of the main drawbacks of this algorithm for optimizing real﹚orld problems was introduced. In summary, they showed that GWO's performance degrades as the optimal solution of the problem diverges from 0. In this paper, by introducing a straightforward modification to the original GWO algorithm, that is, neglecting its social hierarchy, the authors were able to largely eliminate this defect and open a new perspective for future use of this algorithm. The efficiency of the proposed method was validated by applying it to benchmark and real﹚orld engineering problems.

2 部分代码

​​​clcclear​global NFENFE=0;​nPop=30;    % Number of search agents (Population Number)MaxIt=1000; % Maximum number of iterationsnVar=30;    % Number of Optimization Variables nFun=1;     % Function No, select any integer number from 1 to 14​CostFunction=@(x,nFun) Cost(x,nFun);        % Cost Function​%% Problem Definition​VarMin=-100;             % Decision Variables Lower Boundif nFun==7    VarMin=-600;             % Decision Variables Lower Boundendif nFun==8    VarMin=-32;             % Decision Variables Lower Boundendif nFun==9    VarMin=-5;             % Decision Variables Lower Boundendif nFun==10    VarMin=-5;             % Decision Variables Lower Boundendif nFun==11    VarMin=-0.5;             % Decision Variables Lower Boundendif nFun==12    VarMin=-pi;             % Decision Variables Lower Boundendif nFun==14    VarMin=-100;             % Decision Variables Lower BoundendVarMax= -VarMin;             % Decision Variables Upper Boundif nFun==13    VarMin=-3;             % Decision Variables Lower Bound    VarMax= 1;             % Decision Variables Upper Boundend​%%   Grey Wold Optimizer (GWO)​% Initialize Alpha, Beta, and DeltaAlpha_pos=zeros(1,nVar);Alpha_score=inf;​Beta_pos=zeros(1,nVar);Beta_score=inf;​Delta_pos=zeros(1,nVar);Delta_score=inf;​%Initialize the positions of search agentsPositions=rand(nPop,nVar).*(VarMax-VarMin)+VarMin;BestCosts=zeros(1,MaxIt);​fitness=nan(1,nPop);​iter=0;  % Loop counter​%% Main loopwhile iter<MaxIt    for i=1:nPop                % Return back the search agents that go beyond the boundaries of the search space        Flag4ub=Positions(i,:)>VarMax;        Flag4lb=Positions(i,:)<VarMin;        Positions(i,:)=(Positions(i,:).*(~(Flag4ub+Flag4lb)))+VarMax.*Flag4ub+VarMin.*Flag4lb;                % Calculate objective function for each search agent        fitness(i)= CostFunction(Positions(i,:), nFun);                % Update Alpha, Beta, and Delta        if fitness(i)<Alpha_score            Alpha_score=fitness(i);  % Update Alpha            Alpha_pos=Positions(i,:);        end                if fitness(i)>Alpha_score && fitness(i)<Beta_score            Beta_score=fitness(i);  % Update Beta            Beta_pos=Positions(i,:);        end                if fitness(i)>Alpha_score && fitness(i)>Beta_score && fitness(i)<Delta_score            Delta_score=fitness(i);  % Update Delta            Delta_pos=Positions(i,:);        end    end        a=2-(iter*((2)/MaxIt));  % a decreases linearly fron 2 to 0        % Update the Position of all search agents    for i=1:nPop        for j=1:nVar                        r1=rand;            r2=rand;                        A1=2*a*r1-a;            C1=2*r2;                        D_alpha=abs(C1*Alpha_pos(j)-Positions(i,j));            X1=Alpha_pos(j)-A1*D_alpha;                        r1=rand;            r2=rand;                        A2=2*a*r1-a;            C2=2*r2;                        D_beta=abs(C2*Beta_pos(j)-Positions(i,j));            X2=Beta_pos(j)-A2*D_beta;                        r1=rand;            r2=rand;                        A3=2*a*r1-a;            C3=2*r2;                        D_delta=abs(C3*Delta_pos(j)-Positions(i,j));            X3=Delta_pos(j)-A3*D_delta;                        Positions(i,j)=(X1+X2+X3)/3;                    end    end        iter=iter+1;    BestCosts(iter)=Alpha_score;        fprintf('Iter= %g,  NFE= %g,  Best Cost = %g\n',iter,NFE,Alpha_score); end​

3 仿真结果

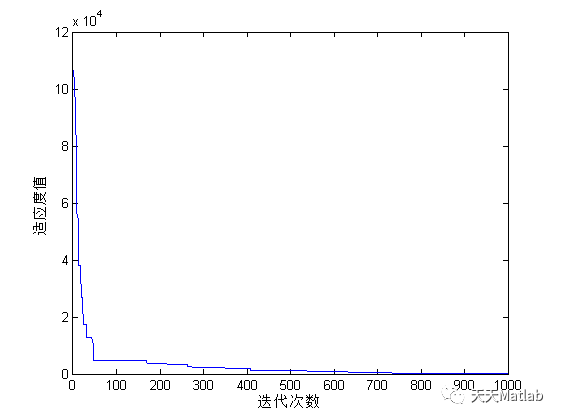
4 参考文献

[1] Akbari E ,  Rahimnejad A ,  Gadsden S A . A greedy non﹉ierarchical grey wolf optimizer for real﹚orld optimization[J]. Electronics Letters, 2021(1).​

博主简介：擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真，相关matlab代码问题可私信交流。

部分理论引用网络文献，若有侵权联系博主删除。

5 代码下载