从线段树到树状数组
对于一个数组nums,我们要完成两个操作
- 修改其中某个元素的值(单点修改)
- 求出前n个元素的和(区间求和)
对于数组nums,单点修改的时间复杂度为O(1)\mathcal{O}(1)O(1),区间求和为O(n)\mathcal{O}(n)O(n)

对于前缀和,可以得到数组prenums,该数组区间求和时间复杂度为O(1)\mathcal{O}(1)O(1),单点修改为O(n)\mathcal{O}(n)O(n)

能不能考虑一个折中的办法,让单点修改和区间求和的方法都不那么慢?
有人考虑用线段树来完成这两个操作,把数字两两求和,保存在另一个数组中,然后逐层向上,重复操作,变成类似二叉树的结构。
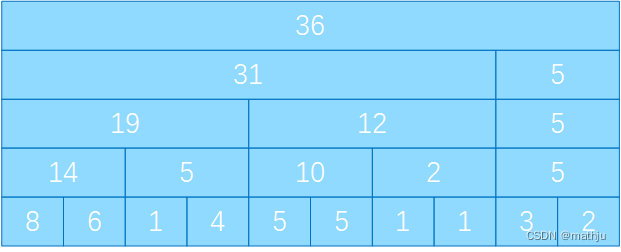
此时如果计算前15个数字的和,只计算前4个数字即可(8+4+2+1),这样加快了查询的时间。
而且我们发现有些数据是不需要使用的,例如左端的14和5,在计算前三个数和,前四个数和时,不需要使用5,而计算前5个数组时使用上方的19更好,所以5在这里不需要使用。
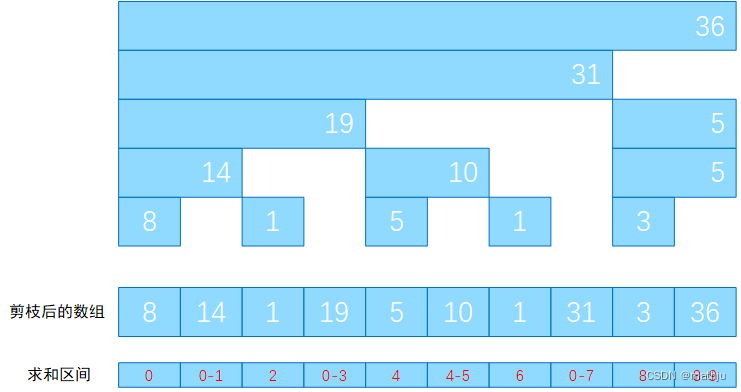
类似还有很多这样的数字,我们对这个线段树进行剪枝,我们可以得到下面的结构。我们还发现剩下的数据量与原数组相等,这样我们可以将这些数据正好放入一个数组中,这个数组与原数组一样长。这种数组就称为树状数组,该数组中每一个元素都对应下面的一个区间,每个区间表示的是原数组的区间和,求和时找到对应区间求和,修改时向上找到包含它的区间进行修改即可。
树状数组介绍
树状数组(Binary Indexed Tree, Fenmick Tree),它对数组进行区间划分,是一种用于高效求解前缀和的数据结构,它的单点修改和区间求和的时间复杂度为O(logn)\mathcal{O}(\log n)O(logn)。
树状数组单点修改和区间求和的实现
树状数组在原数组的基础上划分区间保存区间和,例如,数列有9个元素,分别用a[1],a[2],⋯ ,a[9]a[1],a[2],\cdots,a[9]a[1],a[2],⋯,a[9]存储,树状数组引入数组c[]c[]c[]保存一个或多个元素和,因为数组c[]c[]c[]可以用树状结构表示,因此c[]c[]c[]称为树状数组。
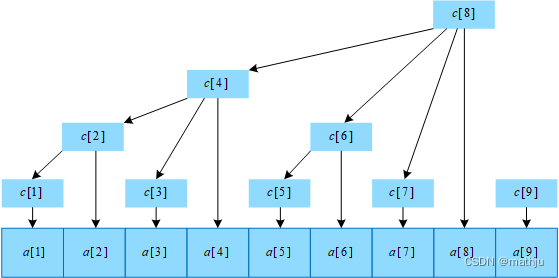
区间长度
树状数组通过二进制分解划分区间,对于c[i]c[i]c[i],若iii的二进制表示中末尾有kkk个连续的0,则c[i]c[i]c[i]存储的区间长度为2k2^k2k,区间为a[i]a[i]a[i]起始向前数2k2^k2k个元素,即c[i]=a[i−2k+1]+a[i−2k+2]+⋯+a[i]c[i] = a[i - 2^k + 1] + a[i - 2^k + 2] + \cdots + a[i]c[i]=a[i−2k+1]+a[i−2k+2]+⋯+a[i]。
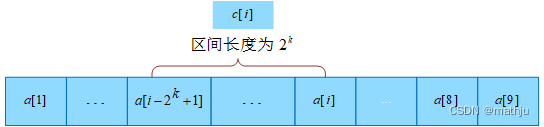
区间长度就是i的二进制表示下最低位的1及它后面的0构成的数值。
例如i=20,其二进制表示为10100,末尾有两个0,区间长度为222^222,其实就是10100最低位1及其后面的0构成的数值(100)2(100)_2(100)2,十进制为4。
已知一个十进制数iii,如何求其区间长度
以i=20i = 20i=20为例,将i取反,得∼i=01011\sim i = 01011∼i=01011,∼i+1=01100\sim i + 1 = 01100∼i+1=01100,之后(∼i+1)&i=(01100)2&(10100)2=(00100)2(\sim i + 1) \& i=(01100)_{2}\&(10100)_{2}=(00100)_{2}(∼i+1)&i=(01100)2&(10100)2=(00100)2
在计算机中,-i的补码正好是∼i+1\sim i + 1∼i+1
c[i]c[i]c[i]存储的区间长度lowbit(i)=(−i)&ilowbit(i)=(-i)\&ilowbit(i)=(−i)&i
前驱和后继
直接前驱:c[i]c[i]c[i]的直接前驱为c[i−lowbit(i)]c[i -lowbit(i)]c[i−lowbit(i)],即c[i]c[i]c[i]左侧紧邻的子树的根。
直接后继:c[i]c[i]c[i]的直接后继为c[i+lowbit(i)]c[i +lowbit(i)]c[i+lowbit(i)],即c[i]c[i]c[i]的父节点。
前驱:c[i]c[i]c[i]的直接前驱、其直接前驱的直接前驱等,即c[i]c[i]c[i]左侧所有子树的根。
后继:c[i]c[i]c[i]的直接后继,其直接后继的直接后继等,即c[i]c[i]c[i]的所有祖先。
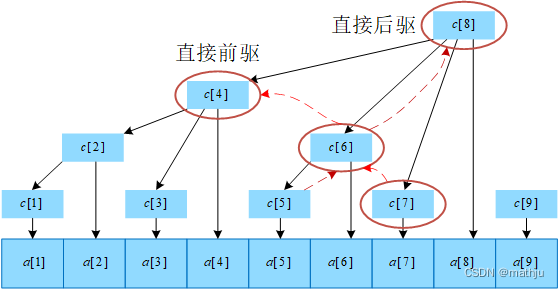
c[7]c[7]c[7]的直接前驱为c[6]c[6]c[6],c[6]c[6]c[6]的直接前驱为c[4]c[4]c[4],c[4]c[4]c[4]没有直接前驱;c[7]c[7]c[7]的前驱为c[6]c[6]c[6]、c[4]c[4]c[4]。
c[5]c[5]c[5]的直接后继为c[6]c[6]c[6],c[6]c[6]c[6]的直接后继为c[8]c[8]c[8],c[8]c[8]c[8]没有直接后继;c[5]c[5]c[5]的后继为c[6]c[6]c[6]、c[8]c[8]c[8]。
查询前缀和
前iii个元素的前缀和sum[i]sum[i]sum[i]等于c[i]c[i]c[i]加上c[i]c[i]c[i]的前驱,
sum[7]sum[7]sum[7]等于c[7]c[7]c[7]加上c[7]c[7]c[7]的前驱,c[7]c[7]c[7]的前驱为c[6]c[6]c[6]、c[4]c[4]c[4],因此sum[7]=c[7]+c[6]+c[4]sum[7]=c [7]+c [6]+c [4]sum[7]=c[7]+c[6]+c[4]。
点更新
若对a[i]a[i]a[i]进行修改,令a[i]a[i]a[i]加上一个数zzz,则只需更新c[i]c[i]c[i]及其后继(祖先),即令这些节点都加上zzz即可,无需修改其他节点。
例如,修改a[5]a[5]a[5],令其加222。只需c[5]+2c[5]+2c[5]+2,然后c[5]c[5]c[5]的后继分别加222,即c[6]+2c[6]+2c[6]+2、c[8]+2c[8]+2c[8]+2。
查询区间和
若求区间和值a[i]+a[i+1]+…+a[j]a[i]+a[i+1]+…+a[j]a[i]+a[i+1]+…+a[j],则求解前jjj个元素的和值减去前i−1i-1i−1个元素的和值即可,即sum[j]−sum[i−1]sum[j]-sum[i-1]sum[j]−sum[i−1]。
算法分析
前缀和:求a[1]⋯a[i]a[1]\cdots a[i]a[1]⋯a[i]的前缀和,普通数组O(n)\mathcal O(n)O(n),树状数组O(logn)\mathcal O(\log n)O(logn)。
区间和:求a[1]⋯a[j]a[1]\cdots a[j]a[1]⋯a[j]的区间和,普通数组O(n)\mathcal O(n)O(n),树状数组O(logn)\mathcal O(\log n)O(logn)。
点更新:修改a[i]a[i]a[i]加上zzz,普通数组O(1)\mathcal O(1)O(1),树状数组O(logn)\mathcal O(\log n)O(logn)。
程序实现
class BinaryIndexTree:
def __init__(self, nums: List[int]):
self.tree = [0] + nums
# 构造出的BIT空间比原nums多一,第1个下标0不用
n = len(nums)
for i in range(1, n + 1):
j = i + self.lowbit(i)
if j < n + 1:
self.tree[j] += self.tree[i]
def update(self, index: int, val: int) -> None:
prev = self.sumRange(index, index)
index += 1
val -= prev
while index < len(self.tree):
self.tree[index] += val
index += self.lowbit(index)
def sumRange(self, left: int, right: int) -> int:
return self.presum(right) - self.presum(left - 1)
def lowbit(self, x: int) -> int:
return x & -x
#自定义前缀和preSum函数
def presum(self, index: int) -> int:
index += 1
res = 0
while index:
res += self.tree[index]
index -= self.lowbit(index)
return res
LeetCode 面试题10.10 数字流的秩
tree数组序号为输入数字,数组数字为数字的次数,通过树状数组做统计。
class StreamRank:
def __init__(self):
self.tree = [0]*50002
def track(self, x: int) -> None:
x += 1 # x = 0时会陷入死循环
while x < 50002:
self.tree[x] += 1
x += x & -x
def getRankOfNumber(self, x: int) -> int:
x += 1
res = 0
while x:
res += self.tree[x]
x -= -x & x
return res
LeetCode307 区域和检索-区间可修改
BIT数组初始化有点技巧,需要多看看加深理解
class NumArray:
def __init__(self, nums: List[int]):
self.tree = [0] + nums
n = len(nums)
for i in range(1, n + 1):
j = i + self.lowbit(i)
if j < n + 1:
self.tree[j] += self.tree[i]
def update(self, index: int, val: int) -> None:
prev = self.sumRange(index, index)
index += 1
val -= prev
while index < len(self.tree):
self.tree[index] += val
index += self.lowbit(index)
def sumRange(self, left: int, right: int) -> int:
return self.presum(right) - self.presum(left - 1)
def lowbit(self, x: int) -> int:
return x & -x
def presum(self, index: int) -> int:
index += 1
res = 0
while index:
res += self.tree[index]
index -= self.lowbit(index)
return res
致谢
感谢女朋友在绘制图片的帮助





 博客介绍了从线段树到树状数组的演变过程。为解决数组单点修改和区间求和的效率问题,通过对线段树剪枝得到树状数组。详细阐述了树状数组的区间划分、单点修改和区间求和的实现方法,还进行了算法分析,并给出了相关程序实现示例。
博客介绍了从线段树到树状数组的演变过程。为解决数组单点修改和区间求和的效率问题,通过对线段树剪枝得到树状数组。详细阐述了树状数组的区间划分、单点修改和区间求和的实现方法,还进行了算法分析,并给出了相关程序实现示例。
















 1085
1085

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








