根轨迹分析

最新推荐文章于 2025-02-14 14:15:21 发布

纯良FOC

最新推荐文章于 2025-02-14 14:15:21 发布

阅读量3.2k

点赞数 8

分类专栏： MATLAB 控制理论MATLAB教程文章标签： matlab

本文链接：https://blog.youkuaiyun.com/m0_46732561/article/details/125071441

版权

MATLAB 同时被 2 个专栏收录

13 篇文章

订阅专栏

控制理论MATLAB教程

6 篇文章

订阅专栏

本章介绍生成根轨迹图并从这些图形获得相关信息的MATLAB方法。

对于上述系统，它的闭环传递函数为

$\frac{C(s)}{R(s)}=\frac{G(s)}{1+G(s)H(s)}$

令右端的分母为0，得到系统的闭环特征方程，即：

${1+G(s)H(s)}=0$

多数情况下， $G(s)H(s)$ 包含参数增益K，将其表示成零极点形式，则特征方程为

$1+\frac{K(s+z_{1})(s+z_{2})...(s+z_{m})}{(s+p_{1})(s+p_{2})...(s+p_{n})}=0$

或者写成

$1+K\frac{num}{den}=0$

则有

${G(s)H(s)}=-1$

即系统的根轨迹方程。

$\angle -1=\pm 180^{\circ}(2k+1) (k=0,1,2,...)$

$\left | -1 \right |=1$

根据这两个式子确定系统的相角条件和幅值条件。

同时满足幅角条件和幅值条件的s值就是特征方程的根，或者说闭环极点。只满足幅角条件的点在复平面上的轨迹是根轨迹。系统的根轨迹是闭环极点在增益K从0变化到无穷大时的轨迹。

绘制根轨迹

通常用来绘制根轨迹的MATLAB命令是

rlocus(num,den)

该命令在屏幕上绘制根轨迹图。增益K的值是自动确定的(向量K包含了为其计算闭环极点的所有增益值)。

对以状态空间形式定义的系统，rlocus(A, B. C, D)按照自动确定的增益向量来绘制该系统的根轨迹。

应注意的是，命令

rlocus(num,den,K)和 rlocus(A,B,C,D,K) 可以采用用户提供的增益向量K来绘制根轨迹。

如果调用命令时带有左端参数，如

[r,K] = rlocus(num,den)

[r,K] = rlocus(num,den,K)

[r,K] = rlocus(A,B,C,D)

[r,K] = rlocus(A,B,C,D,K)

[r,K] = rlocus(sys)

那么屏幕上将会显示矩阵r和增益向量K( r的行数等于K的长度，列数为n,这里n是分母的次数。r包含根的位置，矩阵r的每一行对应于向量K中的一个增益。绘图命令

plot(r,'-')

可以绘制根轨迹。

最后要注意，由于增益向量是自动确定的，所以

$G(s)H(s)=\frac{K(s+1)}{s(s+2)(s+3)}$

$G(s)H(s)=\frac{10K(s+1)}{s(s+2)(s+3)}$

$G(s)H(s)=\frac{100K(s+1)}{s(s+2)(s+3)}$

的根轨迹图完全相同。对这3个系统而言，系统的num和den都是一样的。

已知系统如图所示。用正方形的平面形状来绘制根轨迹，使斜率为1的直线正好为 $45^{\circ}$ .现将根轨迹的绘制区间选为

$-6\leqslant x\leqslant 6,-6\leqslant y\leqslant 6$

其中x和y分别是实轴坐标和虚轴坐标。

新建脚本文件：

%a=s(s+1): b=s^2+4s+16
a=[1 1 0];
b=[1 4 16];
%conv(a,b)是给出两个多项式a和b的乘积
c=conv(a,b);
 den=[1 5 20 16 0];
num=[1 3];
r=rlocus(num,den);
plot(r,'-');
%将给定的屏幕绘图设置成正方形
plot(r,'-');v=[-6 6 -6 6];axis(v);axis('square')
grid
title('Root-Locus Plot of G(s) = K(s+3)/[s(s + 0.5)(s^2+4s+16)]')
xlabel('Real Axis');ylabel('lmagAxis') 
%可以做figure上手动标注出零极点位置
gtext('o')
gtext('x')
gtext('x')
gtext('x')
gtext('x')

已知系统结构为：

$\dot{x}=Ax+Bu$

$y=Cx+Du$

$u=r-y$

可以采用命令：

[num,den] = ss2tf(A,B,C,D)

转换为上述形式求解。

同样，这个系统的根轨迹图可以利用MATLAB命令

rlocus(A,B,C,D)

来绘制。

带有极坐标网格线的根轨迹图

为了利用MATLAB在根轨迹图上绘制等 $\zeta$ 直线轨迹和等 $w_{n}$ 圆轨迹，可以采用命令sgrid。

命令sgrid将等阻尼系数（ $\zeta$ = 0 ~ 1,步长0. 1）的直线轨迹和等 $w_{n}$ 的圆轨迹重叠绘制在根轨迹图上。

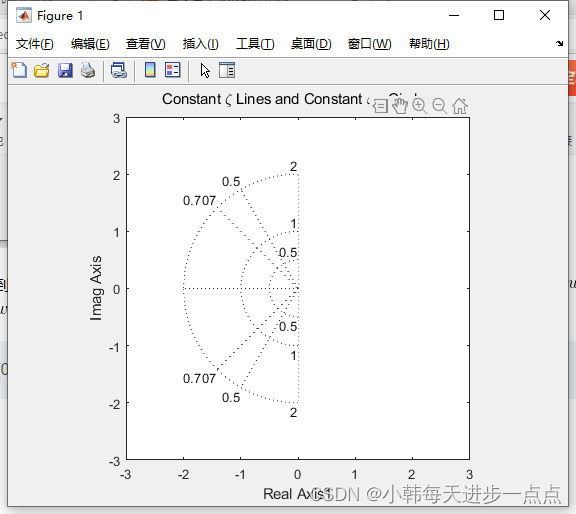
>> v = [-3 3 -3 3]; axis(v); axis('square')
>> sgrid
>> title('Constant \zeta Lines and Constant \omega_n Circles')
>> xlabel('Real Axis1')
>> ylabel('Imag Axis')

得到图形：

如果希望得到特定的 $\zeta$ 的直线轨迹(如 $\zeta$ =0.5的直线和 $\zeta$ =0. 707的直线)及特定的殊的圆轨迹(如 $w_{n}$ =0.5的圆、 $w_{n}$ =1的圆和 $w_{n}$ =2的圆)，可以采用如下命令：

>> sgrid([0.5, 0.707], [0.5, 1, 2])

如果希望将等 $\zeta$ 直线轨迹和等 $w_{n}$ 圆轨迹重叠到系统

num = [0 0 0 1]
den = [1 4 5 0]

的根轨迹图上，只需要在原先绘制根轨迹代码的基础上加上代码

>> sgrid([0.5, 0.707], [0.5, 1, 2])

如果要删去全部等 $\zeta$ 直线轨迹或全部等 $w_{n}$ 圆轨迹，就可以在命令sgrid的参数中采用空括号[]。如果只希望在根轨迹图上重叠与 $\zeta$ =0.5相应的等阻尼系数直线，而不需要等 $w_{n}$ 圆，就可以采用命令

sgrid(0.5,[])

求根轨迹上任意点的增益值K

求根轨迹上任意点的増益K。在闭环系统的MATLAB分析中，经常希望求根轨迹上任意点的增益值K。这可以采用命令

[K,r] = rlocfind(num, den)或[K, r] = rlocfind(A,B,C,D)

之一来完成，其中r是闭环极点。命令rlocfind(必须在rlocus之后调用)将可移动的x-y坐标系覆盖在屏幕上。使用鼠标将价x-y坐标系的原点置于根轨迹上希望的点并按鼠标键，MATLAB 就会显示该点的坐标、该点的增益值及与该增益值对应的闭环极点。

如果所选的点不在根轨迹上，那么命令rlocfind就给出该点的坐标、该点的增益值及与这个K 值相应的闭环极点位置。注意，s平面上的每个点都对应一个增益值。

>> num = [1];
>> den = [1 4 5 0];
>> r = rlocus(num,den);
>> plot(r,'-'); v = [-3 1 -2 2]; axis(v); axis('square')
>> grid
>> sgrid(0.5,[]) 
>> [K,r] = rlocfind(num,den)

非最小相位系统的根轨迹图

非最小相位系统。如果系统的所有极点和零点都位于左半S平面，该系统就称为最小相位系统。如果系统至少有一个极点或零点位于右半S平面，该系统就称为非最小相位系统。之所以要采用非最小相位系统这一术语，与该系统在正弦输入下的相移特性有关。

如果T = 1 s, Ta=0.5 s,那么就可以在程序中输入如下

num = [-0.5 1];
den = [1 1 0];
K1 =0:0.01:30;
K2 =30:1:100;
K3 = 100:5:500;
K = [K1 K2 K3];
r = rlocus(num,den,K);
plot(r); v = [-2 6 -4 4]; axis(v); axis('square')
grid
title('Root-Locus Plot of G(s) = K(1-0.5s)/[s(s+1)]')
xlabel('Real Axis'); ylabel('Imag Axis');

条件稳定系统的根轨迹图

绘制方法同上，利用劳斯判据判断条件稳定条件。

具有传输时延的系统的根轨迹

死时间的MATLAB近似。

为了处理死时间 $e^{-Ts}$ ，MATLAB采用以法国数学家Henri EugfenePad&命名的帕代近似。例如，如果T = 0.1 s,采用三阶传递函数来近似 $e^{-Ts}$ 则可以在计算机中输入如下MATLAB程序：

>> [num,den] = pade(0.1,3);
printsys(num, den, 's')
 
num/den = 
 
   -1 s^3 + 120 s^2 - 6000 s + 120000
   ----------------------------------
     s^3 + 120 s^2 + 6000 s + 120000

类似地，当T = 0.1s时，四阶传递函数近似的程序是

[num,den] = pade(0.1, 4);

printsys(numz den, 's')

控制系统校正的根轨迹方法

控制系统的基本设计方面主要是用解析手段完成的，只有少部分可以采用MATLAB进行。但是，系统设计一旦完成，就必须仔细检査数学模型的响应特性。MATLAB在这方面会起重要作用。

采用根轨迹方法的串联校正技术(如超前校正、滞后校正和超前滞后校正)，以及采用根轨迹方法的并联校正技术。

我是小韩每天进步一点点，一名研0的研究生，刚开始写博客。希望和大家多多交流，一起进步！

求朋友点赞、收藏、关注哈，鼓励一下新人博主，或者提出建议。