两轮自平衡机器人（二）---PID控制

最新推荐文章于 2025-03-26 09:43:01 发布
最新推荐文章于 2025-03-26 09:43:01 发布
阅读量3.5k 收藏 46
点赞数 20
分类专栏： MATLAB/Simscape Multibody 文章标签： matlab/simscape 物理建模 pid控制
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/m0_46652448/article/details/114924918
版权

该控制主要构成的控制环包含三部分，第一个是我们的系统，从中我们将测量倾角，此循环的第二部风是求和过程，在这里我们要比较测量角与期望的输出（0度），我们将此错误输入此循环的第三部分，那就是pid控制器，它将给我们适当的力以稳定机器人，现在我们将开始操作

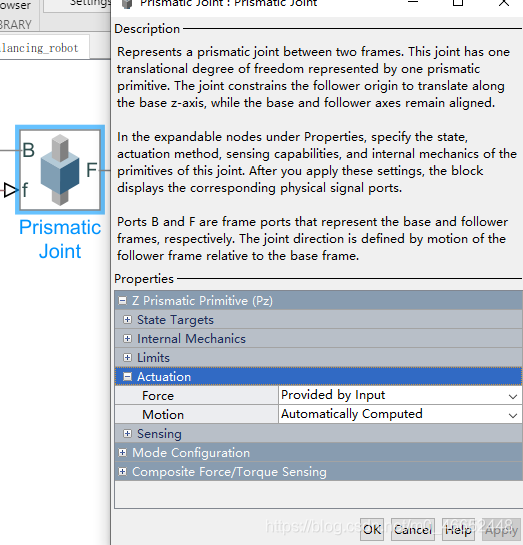
底盘的倾角由旋转关节的位置测量，我们还将通过输入提供棱柱形关节，并自动进行运动的计算，角度以弧度为单位，所以也许您想将其转换成为度数以获得可读性更强的信息，可以通过乘以180来完成

 

 

最后一个阶段就是调节PID参数，必须调整以给我们所需的行为，所以我们将消除我们先前施加的外力，然后给机器人一个初始的倾角而不是施加外力，所以我们将输出信号求和，步进信号将只有10度，在0.01秒内。

PID参数自动调节

调整后的pid参数

我们可以设置响应的理想属性，自动调谐器会产生适当的pid增益，这使我们可以更好的控制机器人，现在机器人仅靠两个轮子保持平衡，你可以走得更远并增强pid参数。

 

 

 

 

编辑不易，如果您觉得对您有用，请点个赞再走吧，谢谢

独轮自平衡机器人双闭环非线性PID 控制
01-14
<html dir="ltr"><head><title></title></head><body>针对竖直飞轮独轮自平衡机器人系统, 提出一种用于独轮自平衡机器人的平衡及运动控制的双闭环非线性PID 控制方法(DLNPID), 并给出了该控制方法稳定性的证明. 该控制方法是具有横滚倾角内环、俯仰倾角内环和前向位移外环的双闭环控制, 其中每个控制环均由非线性PID 控制器(NPID) 构成. 实验结果表明, 所提出的基于非线性PID 的双闭环独轮自平衡机器人控制方法具有比线性方法更好的鲁棒性能.</body></html>
【控制】基于PSO优化自整定PID控制器实现自平衡机器人Matlab代码实现
qq_59747472的博客
12-01 651
摘要: 自平衡机器人是一种复杂的非线性系统，其控制策略的选取直接影响其稳定性和性能。本文研究了一种基于粒子群优化算法(PSO)的自整定PID控制器，用于实现自平衡机器人的稳定控制。该方法通过PSO算法优化PID控制器的参数，使其能够适应不同的工作环境和负载变化，从而提高系统的鲁棒性和控制精度。本文详细介绍了自平衡机器人模型的建立、PID控制器的设计、PSO算法的应用以及仿真实验结果，并对结果进行了深入的分析和讨论，最终验证了该方法的有效性及优越性。1. 引言。
【PID控制】基于PSO的自平衡机器人自整定PID控制器附Matlab代码
Matlab245的博客
03-26 777
自平衡机器人作为一种具备动态稳定能力的智能系统，在工业、服务等领域具有广泛的应用前景。PID控制作为一种经典的控制算法，结构简单、易于实现，被广泛应用于自平衡机器人的控制系统中。然而，传统PID控制器的参数整定往往依赖经验或试错法，难以达到最优控制效果。本文深入探讨了基于粒子群优化（PSO）算法的自平衡机器人自整定PID控制器，详细阐述了其理论基础、算法流程以及实现方法，并对该方法的优势、局限性以及未来发展方向进行了分析与展望。自平衡机器人，也称倒立摆机器人，是一种需要维持自身直立状态的动态系统。
【STM32】【HAL库】平衡小车(PID实战2)(三)PID调参
m0_57585228的博客
10-02 3292
平衡车作为经典PID设计项目,非常热门,也非常适合 PID/单片机 初学的项目没有看起来那么难,愿每个人都可做出自己的平衡车本系列文章,从硬件到软件,带领大家制作平衡小车分为三节硬件设计软件设计PID调参本节是PID调参部分。
两轮平衡车资料(stm32+mpu6050 的PID控制方案)
12-22
很久之前做的一些两轮平衡车资料，主要是一些文档，也有部分的驱动代码
双足机器人的平衡控制
weixin_34008933的博客
04-12 3191
　　在最开始，双足机器人使用的平衡控制策略是「静态步行」（static walking）。这种策略的特点是：机器人步行的过程中，重心（COG，Center of Gravity）的投影始终位于多边形支撑区域（support region）内，这种控制策略的好处在于：机器人可以在行走动作中停止而不摔倒，但代价是行动速度非常迟缓（每一步需要花费10 秒甚至更长，因为需要保持重心的投影始终位于支撑区域，...
玩转OpenHarmony PID：教你打造两轮平衡车
OpenHarmony_dev的博客
12-16 1857
两轮平衡车的控制主要涉及三个PID环的串联使用，它们分别是直立环（平衡控制）、速度环（速度控制）、转向环（方向控制）。P比例参数：该参数能够快速让小车达到平衡状态，但是由于控制是滞后的，以及是惯性系统，容易带来超调，即小车会出现前后摇摆的现象。D微分参数：平衡小车维持的是倾斜角度要为平衡角度，由于PI参数使小车振荡，小车会出现前后摇摆现象，加入D微分参数能够消除小车的振荡。I积分参数：小车由于摩擦力或者风阻力，并且P不能太大，只靠P控制有可能达不到稳定状态，所以需要加入I积分参数，消除稳态误差；
两轮自平衡小车（卡尔曼滤波代码+PID调试文档）
04-01
两轮自平衡小车（卡尔曼滤波代码+PID调试文档），包含详细的代码，stm32为控制器。
轮腿机器人的PID控制
zephyr_wang的博客
08-16 3510
红色箭头形成闭环控制，保持平衡并有速度。当静态平衡时，就只需要平衡PID，无需无刷电机和速度PID
带步进电机的两轮自平衡机器人。-项目开发
03-30
标题中的“带步进电机的两轮自平衡机器人”是一个基于微控制器的智能系统，它利用步进电机来实现两轮直立平衡。这个项目旨在设计一个能够自主保持平衡并可由操纵杆控制的机器人。描述中提到的关键技术包括微步控制、...
两轮平衡车简单串级PID
06-03
本人大一 最近做了两轮平衡小车主控芯片为STM32F103RCT6，局限于本人大一能力有限，但是我决定将他传上来赚点积分去下载我需要的东西，需要的可以下载，注解挺详细的。也可私聊本QQ:1006348650
YACHACK_OPENCV:使用OPENCV，P控制和PID控制的Python代码，用于4WD或2WD机器人的操作
03-28
YACHACK_OPENCV 入门 使用OPENCV在和使用Python进行4WD或2WD机器人操作的代码 安装网络摄像头 访问链接： 安装网络摄像头UVC 在终端中执行： 须藤rmmod uvcvideo sudo modprobe uvcvideo怪癖= 2 （添加imagen终端RPi） 控制PID的工作方式 该算法的执行类似于带有传感器IR的跟随器生产线的算法。
模糊理论和PID相融合的两轮自平衡机器人智能控制系统.pdf
09-08
该系统通过结合模糊理论和PID控制，形成模糊PID控制，以便通过模糊控制弥补PID控制在非线性数学模型方面存在的不足，同时PID控制系统有助于改善模糊控制在两轮自平衡机器人智能控制系统中的效果粗糙、无法精确控制的...
pid控制器代码matlab-AutomatedBalancingRobot:自动平衡机器人是一个项目，其中建造了一个两轮机器人，并将其编程为
05-27
自动平衡机器人是一个项目，其中建造了一个两轮机器人，并将其编程为可从Android应用程序进行无线电控制，同时执行自平衡任务。 该项目使用Matlab来计算完美的PD控制器（采用原始PID控制器结构）和C ++编码语言，以...
两轮自平衡机器人最终doc.doc
07-13
通过分析两轮自平衡机器人的运动规律，采用 PID 控制算法设计了机器人 PID 控制器，实现了机器人的动态自平衡，提高了抗干扰能力，并通过实验验证了算法在自平衡、抗干扰和调整时间上的优势。 此外，本文还提出了两...
基于STM32+PID控制两轮智能自平衡小车设计
热门推荐
毕业作品网站
09-20 1万+
设计一款两轮自平衡小车，通过对陀螺仪的数据的读取处理，从而识别出车身姿态，根据车身姿态计算PID，通过对小车进行实时的PID控制，使得小车可以按照要求实现自主平衡，根据遥控可以实现平稳前进后退；根据灰度传感器数据，可以实现循迹和避障。
【轮式平衡机器人】——角度/速度/方向控制分析&软件控制框架
weixin_51658186的博客
01-21 2705
轮式平衡机器人具有自不稳定性，可类比一级倒立摆系统的控制方法，常见有反馈线性化方法、非线性PID控制、自适应控制、自抗扰控制，还有改进的传统缺乏对外界干扰和参数改变鲁棒性的滑模变结构控制。我们采用较为简单的实现平衡模型。
STM32两轮自平衡小车——PID
fisheader的博客
03-09 3939
#include "control.h" float Med_Angle = -1.4; //»úеÖÐÖµ float Vertical_Kp = -348, //Ö±Á¢»·Kp Vertical_Kd = -0.9; //Ö±Á¢»·Kd£¨´ýµ÷£© float Velocity_Kp = 0.35, //ËٶȻ·Kp£¨´ýµ÷£© Velocity_Ki = 0.00175; //ËٶȻ·Ki£¨´ýµ÷£© float Turn_Kp
平衡小车PID控制
m0_57333603的博客
04-24 3861
在不加外力的情况下，由于重力的作用，双轮小车不会平衡地立在地上，肯定会左右倾倒。为了使小车平衡，需要加入直立环，速度环和转向换三种PID控制。
sw双轮足机器人模型
最新发布
04-03
### 双轮足机器人模型设计方案 双轮足机器人是一种基于两轮平衡原理的移动平台，其设计涉及机械结构、控制算法以及动力学建模等多个方面。以下是关于双轮足机器人模型的设计方案及相关仿真工具的内容。 #### 1. 动力学建模 双轮足机器人的运动可以被描述为倒立摆系统的一种形式。该系统的动态方程通常通过拉格朗日方法推导得出[^1]。假设机器人具有质量 \(m\) 和惯性矩 \(I\)，则可以通过以下公式表示其基本的动力学特性： \[ M(q)\ddot{q} + C(q,\dot{q})\dot{q} + G(q) = \tau \] 其中： - \(M(q)\): 质量矩阵； - \(C(q, \dot{q})\): 科氏力和离心力项； - \(G(q)\): 重力向量； - \(\tau\): 控制输入扭矩； 对于简化版的单自由度双轮机器人，可进一步得到如下线性化状态空间表达式[^2]: ```python import numpy as np A = np.array([[0, 1], [g/l, -b/m]]) B = np.array([[0], [1/(m*l)]]) ``` 上述代码片段展示了如何构建一个简单的状态空间模型用于控制系统分析。 #### 2. 平衡控制器设计 为了使双轮足机器人保持直立并稳定运行，PID控制器或LQR（Linear Quadratic Regulator）是最常用的两种策略之一。LQR能够优化性能指标函数中的权值参数来实现更优的稳定性表现[^3]。 #### 3. 仿真环境搭建 (SolidWorks Simulation) 利用 SolidWorks 进行三维实体造型的同时还可以借助内置插件完成有限元分析(FEA)，从而验证实际物理尺寸下的应力分布情况是否满足需求。此外，在多体动力学模块中也可以模拟整个装置的工作过程以便调整初始条件或者测试不同场景下响应行为的变化趋势[^4]。 ---
评论 16
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

水月流萤

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值