ACM-BFS之胜利大逃亡——hdu1253

最新推荐文章于 2020-10-06 14:59:29 发布
原创 最新推荐文章于 2020-10-06 14:59:29 发布 · 4.5k 阅读 · 4 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#ACM #BFS #胜利大逃亡 #hdu1253

这是一道简单的ACM竞赛题目，主要运用广度优先搜索（BFS）策略。问题扩展到三维空间，需要考虑六个方向的移动：前后左右上下。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

胜利大逃亡
题目： http://acm.hdu.edu.cn/showproblem.php?pid=1253
Problem Description
Ignatius被魔王抓走了,有一天魔王出差去了,这可是Ignatius逃亡的好机会.

魔王住在一个城堡里,城堡是一个A*B*C的立方体,可以被表示成A个B*C的矩阵,刚开始Ignatius被关在(0,0,0)的位置,离开城堡的门在(A-1,B-1,C-1)的位置,现在知道魔王将在T分钟后回到城堡,Ignatius每分钟能从一个坐标走到相邻的六个坐标中的其中一个.现在给你城堡的地图,请你计算出Ignatius能否在魔王回来前离开城堡(只要走到出口就算离开城堡,如果走到出口的时候魔王刚好回来也算逃亡成功),如果可以请输出需要多少分钟才能离开,如果不能则输出-1.


Input
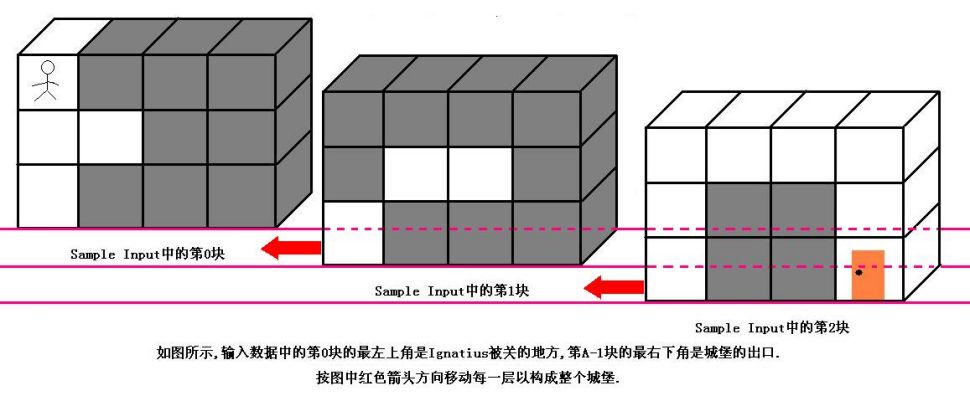
输入数据的第一行是一个正整数K,表明测试数据的数量.每组测试数据的第一行是四个正整数A,B,C和T(1<=A,B,C<=50,1<=T<=1000),它们分别代表城堡的大小和魔王回来的时间.然后是A块输入数据(先是第0块,然后是第1块,第2块......),每块输入数据有B行,每行有C个正整数,代表迷宫的布局,其中0代表路,1代表墙.(如果对输入描述不清楚,可以参考Sample Input中的迷宫描述,它表示的就是上图中的迷宫)

特别注意:本题的测试数据非常大,请使用scanf输入,我不能保证使用cin能不超时.在本OJ
最低0.47元/天 解锁文章

200万优质内容无限畅学
夜深人静写算法（十）- 广度优先搜索
英雄哪里出来
01-12 7万+
寻路算法的鼻祖---广度优先搜索
HDOJ 1253 HDU 1253 胜利大逃亡 ACM 1253 IN HDU
weixin_30357231的博客
08-20 431
MiYu原创, 转帖请注明 : 转载自______________白白の屋题目地址: http://acm.hdu.edu.cn/showproblem.php?pid=1253题目描述:胜利大逃亡Time Limit: 4000/2000 MS (Java/Others)Memory Limit: 65536/32768 K (Java/Others)Total...
Hdoj 1253
weixin_34101229的博客
03-13 150
原题链接 描述 Ignatius被魔王抓走了,有一天魔王出差去了,这可是Ignatius逃亡的好机会. 魔王住在一个城堡里,城堡是一个ABC的立方体,可以被表示成A个B*C的矩阵,刚开始Ignatius被关在(0,0,0)的位置,离开城堡的门在(A-1,B-1,C-1)的位置,现在知道魔王将在T分钟后回到城堡,Ignatius每分钟能从一个坐标走到相邻的六个坐标中的其中一个.现在给你城堡的地图,...
九度OJ题目1456：胜利大逃亡（BFS算法）
风口的猪2016
03-14 687
题目描述： Ignatius被魔王抓走了,有一天魔王出差去了,这可是Ignatius逃亡的好机会.魔王住在一个城堡里,城堡是一个A*B*C的立方体,可以被表示成A个B*C的矩阵,刚开始Ignatius被关在(0,0,0)的位置,离开城堡的门在(A-1,B-1,C-1)的位置,现在知道魔王将在T分钟后回到城堡,Ignatius每分钟能从一个坐标走到相邻的六个坐标中的其中一个.现在给你城堡的地图
HDU1429 胜利大逃亡
永不止步！！！！
08-09 578
这道题用的是广搜，状态压缩，起初不理解状态压缩是怎么回事，一个 点可以被访问多次，怎么就还能找到最短路径？ 现在有所顿悟，每到达一种新的状态就是一个新的开始（把它看作又一 个起点），那么用广搜，起点到终点，是可以找到最短路径的。 #include #include #include using namespace std; char grap[25][
HDU 1429 胜利大逃亡(续) 解题报告
lawk97的博客
09-04 713
HDU 1429的解题报告
ACM-三维BFS之Asteroids!——hdu1240
继续激情，继续奋斗。
04-30 4852
ACM 三维BFS Asteroids! hdu1240
hdu1429 胜利大逃亡(续) （广搜+状态压缩）
671coder的专栏
04-11 4910
题目： 胜利大逃亡(续) 链接： http://acm.hdu.edu.cn/showproblem.php?pid=1429 yy： 本来做了道自己认为不太简单的题很高兴。。但是一看。。夏天的风直接把他归类到搜索level1里面了。。。哎。。这就是差距啊。。。 思路： 广度优先搜索 + 状态压缩 由于只有10把钥匙，所以可以直接用状态压缩来做。。。其他就不说了，其实仔细一看，
HDU 专题分类（2013年8月）
08-07
胜利大逃亡 - **问题描述**：在敌人追捕下，寻找逃离的最佳路线。 - **算法应用**：BFS，用于在敌对环境中寻路，考虑障碍和敌人位置。 以上分析展示了算法竞赛中常见问题类型及其背后的算法原理，这些技能对于提升...
胜利大逃亡
G191018的博客
03-25 409
#include<stdio.h> #include #include<string.h> #include using namespace std; int a,b,c,t,flag; int map[55][55][55],vis[55][55][55]; void dfs(int x,int y,int z,int step) { int i,dx,dy,dz; in...
android写的胜利大逃亡游戏
11-06
android写的胜利大逃亡游戏，架构不错，游戏也挺有意思
hdu_1253_胜利大逃亡(bfs+剪枝)
bin_gege的博客
05-11 458
题目连接：http://acm.hdu.edu.cn/showproblem.php?pid=1253 题意：三维BFS，不解释 题解：DFS+剪枝会超时，裸BFS会超时，BFS+剪枝才能AC，有点伤，我以为数据会让DFS速度快一下，看来是我天真了 #include #include using namespace std; #define FFC(i,a,b) for(int i=a;i<
搜索练习：问题 D: 胜利大逃亡
caixiaobaideye的博客
05-19 326
题目描述 Ignatius被魔王抓走了,有一天魔王出差去了,这可是Ignatius逃亡的好机会.魔王住在一个城堡里,城堡是一个ABC的立方体,可以被表示成A个B*C的矩阵,刚开始Ignatius被关在(0,0,0)的位置,离开城堡的门在(A-1,B-1,C-1)的位置,现在知道魔王将在T分钟后回到城堡,Ignatius每分钟能从一个坐标走到相邻的六个坐标中的其中一个.现在给你城堡的地图,请你计算出Ignatius能否在魔王回来前离开城堡(只要走到出口就算离开城堡,如果走到出口的时候魔王刚好回来也算逃亡成功)
胜利
hu523613的专栏
08-23 480
在实验室紧张地忙碌了三天，终于把论文撰写完毕，这是一个累并快乐得假期。在**组的这些时光里，我学到了太多东西。学术地﹑人生的，都将对我下一步产生重要的影响。感谢所有人！
2017网易游戏雷火盘古实习生招聘笔试真题 推箱子
sth的博客
03-19 766
2018.3.19 此题我用了广度优先搜索(BFS)的方法.广度优先搜索不仅仅可以使用在图的遍历中，而且可以用于求解复杂问题的最优解。引子gnatius被魔王抓走了,有一天魔王出差去了,这可是Ignatius逃亡的好机会.魔王住在一个城堡里,城堡是一个A*B*C的立方体,可以被表示成A个B*C的矩阵,刚开始Ignatius被关在(0,0,0)的位置,离开城堡的门在(A-1,B-1,C-1)的位置,...
HDU1253 胜利大逃亡(DFS)
Whisker_yu的专栏
09-05 1010
这道题貌似大家都是用BFS写的，因为最近在练习DFS，所以就用DFS写了，虽然自己觉得已经剪枝了，但是貌似效果不是很好，还是有1000+ms，以后会用BFS再写一次的 #include #include int dir[6][3]={{1,0,0},{-1,0,0},{0,1,0},{0,-1,0},{0,0,1},{0,0,-1}}; int a,b,c,flag,map[51][51][5
【DFS】胜利大逃亡
qq_45869639的博客
10-06 278
胜利大逃亡 本题用bfs更简单，但是我用的dfs ：） 题意理解 从(0,0,0)出发，在规定时间t内，走到(a-1,b-1,c-1)到达出口，逃亡成功；若未到达出口则逃亡失败，逃亡成功输出逃亡所走的步数，逃亡失败则输出-1。 ※输入地图中0为通路1为墙（一定要认真！！我把1当成通路调了一个小时QWQ) 代码如下 #include <iostream> #include <cstdio> using namespace std; const int maxn = .
杭电oj-----Nightmare(BFS)
smile吖
12-03 503
Nightmare 题目链接:       杭电oj 1702 题目描述: Ignatius had a nightmare last night. He found himself in a labyrinth with a time bomb on him. The labyrinth has an exit, Ignatius should get out of the labyrin...
7-5 胜利大逃亡 ACM
最新发布
12-29
### ACM竞赛‘胜利大逃亡’问题解决方案 #### 背景介绍 动态规划一直是ACM竞赛中的重点，同时又是难点，因为该算法时间效率高，代码量少，多元性强，主要考察思维能力、建模抽象能力、灵活度[^1]。对于特定题目如“胜利大逃亡”，这类问题通常涉及路径寻找或最优解计算。 #### 问题描述 假设在一个迷宫环境中存在多个起点和终点，“胜利大逃亡”的目标是从任意一个起始位置到达至少一个安全出口的位置，并且希望找到最短逃生路线长度。此类问题可以被看作是一个图论上的广度优先搜索(BFS)或者单源最短路径(Dijkstra's Algorithm)求解实例化版本之一。 #### 方法概述 针对这个问题，采用BFS来解决会更加合适一些，因为它能够保证最先访问到的目标节点即为距离最近者；而Dijkstra虽然也可以处理带权边的情况，但对于本题而言显得有些复杂而不必要。具体实现如下： ```python from collections import deque def bfs_escape(maze, start_positions): rows = len(maze) cols = len(maze[0]) directions = [(0,-1), (-1,0), (0,+1), (+1,0)] # 左 上 右 下 queue = deque() visited = set() for pos in start_positions: if maze[pos[0]][pos[1]] != '#': # 如果不是墙，则加入队列 queue.append((pos, 0)) visited.add(pos) while queue: current_pos, steps = queue.popleft() x, y = current_pos # 判断当前位置是否为边界(出口)，如果是则返回步数作为结果 if x == 0 or x == rows - 1 or y == 0 or y == cols - 1: return steps for dx, dy in directions: nx, ny = x + dx, y + dy next_pos = (nx, ny) if 0 <= nx < rows and 0 <= ny < cols \ and next_pos not in visited \ and maze[nx][ny] != '#': queue.append((next_pos, steps + 1)) visited.add(next_pos) return "IMPOSSIBLE" ``` 此段Python代码实现了基于宽度优先遍历的方法去尝试从给定的一个或多个初始坐标出发，在二维字符数组表示的地图上探索是否存在通往地图边缘的安全通道。如果找到了这样的通路，则输出最小移动次数；如果没有可行出路，则报告无法逃脱。
评论 1
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值