【一本通】数星星【BIT】

最新推荐文章于 2024-11-26 14:34:22 发布

原创最新推荐文章于 2024-11-26 14:34:22 发布 · 164 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#c++ #算法

数据结构专栏收录该内容

21 篇文章

订阅专栏

这篇博客介绍了一种解决星星等级统计问题的方法。给定每颗星星的坐标，通过区间求和BIT（Binary Indexed Tree）数据结构，可以高效地计算出每个位置左下方星星的数量，从而得到各级星星的数目。代码实现中，首先读取星星数量及坐标，然后利用BIT进行区间更新和查询，最后输出各级星星的计数。

Date：2022.04.02
题意描述：
天空中有一些星星，这些星星都在不同的位置，每个星星有个坐标。
如果一个星星的左下方（包含正左和正下）有 k 颗星星，就说这颗星星是 k 级的。
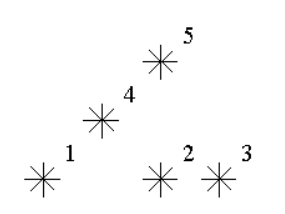
在这里插入图片描述

例如，上图中星星 5 是 3 级的（1,2,4 在它左下），星星 2,4 是 1 级的。
例图中有 1 个 0 级，2 个 1 级，1 个 2 级，1 个 3 级的星星。
给定星星的位置，输出各级星星的数目。
换句话说，给定 N 个点，定义每个点的等级是在该点左下方（含正左、正下）的点的数目，试统计每个等级有多少个点。
输入格式
第一行一个整数 N，表示星星的数目；
接下来 N 行给出每颗星星的坐标，坐标用两个整数 x,y 表示；
不会有星星重叠。星星按 y 坐标增序给出，y 坐标相同的按 x 坐标增序给出。
输出格式
N 行，每行一个整数，分别是 0 级，1 级，2 级，……，N−1 级的星星的数目。
数据范围
1≤N≤15000,
0≤x,y≤32000
输入样例：
5
1 1
5 1
7 1
3 3
5 5
输出样例：
1
2
1
1
0

思路： $y$ 递增，因此每个其前面输入的纵坐标都是<=它的，因此只需找到横坐标<=它的数量即可，区间求和BIT。
代码如下：

#include <bits/stdc++.h>
using namespace std;
const int N = 4e4+10;
typedef long long LL;
LL n,m,tr[N],a[N],cnt[N];
LL lowbit(LL x) {return x&-x;}
void add(LL x,LL c)
{
    for(int i=x;i<=N;i+=lowbit(i)) tr[i]+=c;//注意爬树时要到N
}
LL getsum(LL x)
{
    LL res=0;
    for(int i=x;i;i-=lowbit(i)) res+=tr[i];
    return res;
}
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        LL x,y;cin>>x>>y;
        x++;//bit不适用于下标为0
        cnt[getsum(x)]++;
        add(x,1);
    }
    for(int i=0;i<n;i++) cout<<cnt[i]<<'\n';
    return 0;
}