数据结构--对称二叉树

对称二叉树

给定一个二叉树，检查它是否是镜像对称的。

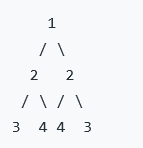
如下图的二叉树就是对称的：

bool func(struct TreeNode* p, struct TreeNode* q) {
 if (p == NULL && q == NULL) {
  return true;
 }
 if (p == NULL || q == NULL) {
  return false;
 }
 return p->val == q->val
  && func(p->left, q->right)
  && func(p->right, q->left);
}
bool isSymmetric(struct TreeNode* root) {
 if (root == NULL) {
  return true;
 }
 return  func(root->left, root->right);
}