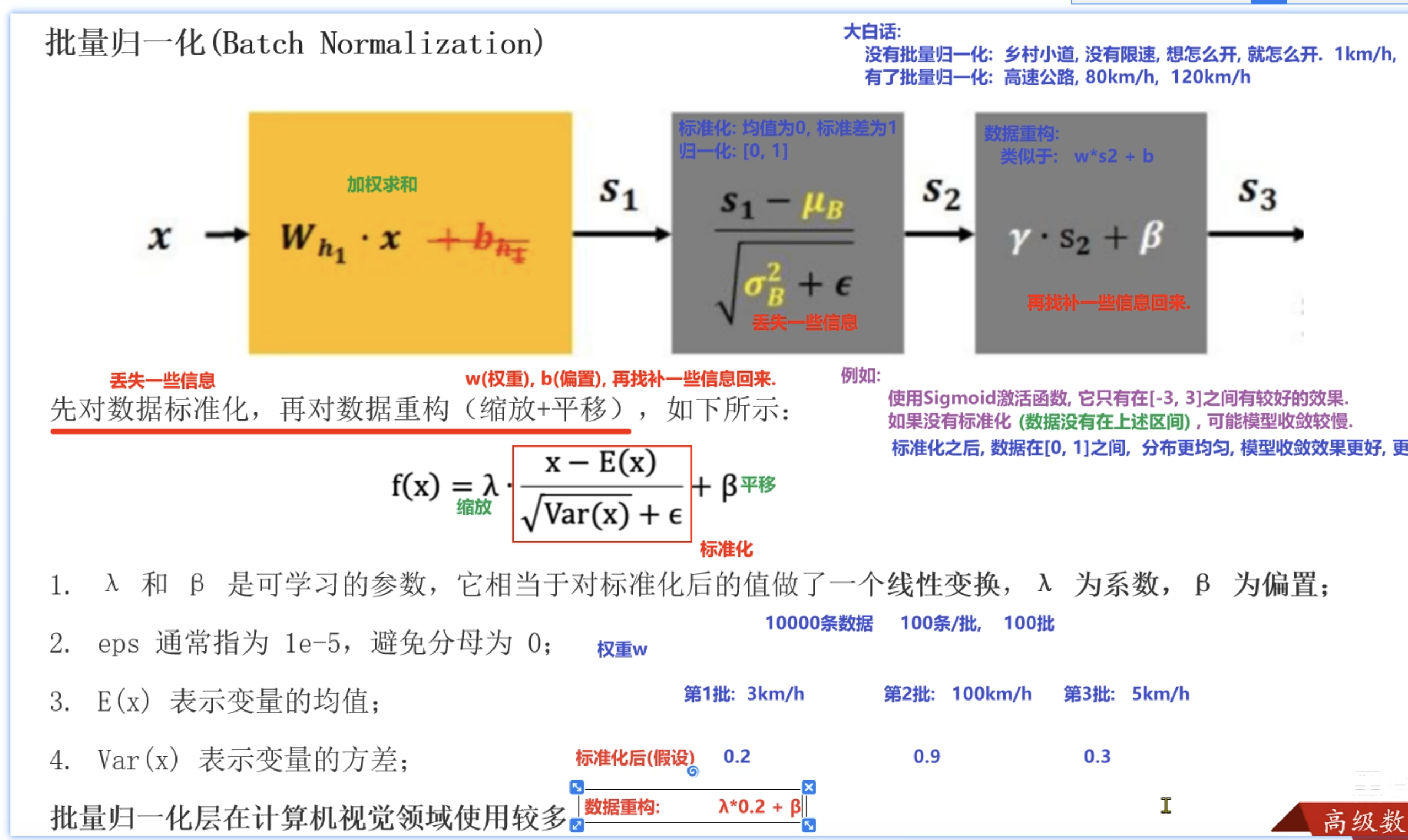
正则化(批量归一化(BN))
- 就是先进行标准化,丢失一些信息,(例如这个给数据3,标准化后为0.2,这样就小了哦,就是丢失了一些信息)
- 然后再进行数据重构,wx+b这种进行找补一些信息回来(例如再给上面的0.2,进行 r*0.2 +β 这种就右放大了,也就找了一些信息回来)
- BN的本质确实是标准化,而不是我们通常说的Min-Max归一化,对于Batch Normalization:确实是标准化 + 可学习重构。只是历史命名的问题:论文作者(Ioffe & Szegedy, 2015)可能为了强调“将数据归一到稳定分布”的目的,深度学习社区早期术语使用比较随意
测试代码
- 任何数据(一维或二维)都可以直接BN
- 但直接BN效果有限,因为没有特征学习
- 特征提取层(Linear/Conv) + BN 才是标准组合
import torch
import torch.nn as nn
# 处理二维数据,直接处理就行
def dm01():
# 一个两通道(就是两个)的 3 * 4 的矩阵
input_2d = torch.randn(1,2,3,4)
print(f'input_2d:{input_2d}')
# 参1 就是几通道,这里就设置多少
# 参2: 噪声值
# 参3: 就是β,动量值
# 参4: 对标准化后的进行缩放和平移
bn2d = nn.BatchNorm2d(2, eps=1e-05, momentum=0.1, affine=True)
output_2d = bn2d(input_2d)
print(f'output_2d:{output_2d}')
pass
# 处理一维数据,需要先进行网络隐藏层的线性处理
def dm02():
# 就是2 *2 的矩阵,处理的就是一行的一维数据
input_1d = torch.randn(2,2)
# 只要输入2就行了,和input_1d的列 2 匹配就行,输出无所谓
linear1 = nn.Linear(2,4)
# 隐藏层线性处理
l1 = linear1(input_1d)
print(f'l1:{l1}')
# 创建Bn层(批量归一化层)
bn1d =nn.BatchNorm1d(num_features=4)
output_1d = bn1d(l1)
print(f'output_1d:{output_1d}')
pass
if __name__ == '__main__':
dm01()
dm02()
测试结果
D:\software\python.exe -X pycache_prefix=C:\Users\HONOR\AppData\Local\JetBrains\PyCharm2025.2\cpython-cache "D:/software/PyCharm 2025.2.4/plugins/python-ce/helpers/pydev/pydevd.py" --multiprocess --qt-support=auto --client 127.0.0.1 --port 54557 --file C:\Users\HONOR\Desktop\python\test26_bn.py
Connected to: <socket.socket fd=1000, family=2, type=1, proto=0, laddr=('127.0.0.1', 54571), raddr=('127.0.0.1', 54557)>.
Connected to pydev debugger (build 252.27397.106)
input_2d:tensor([[[[ 0.7882, 0.6323, -0.1769, -0.5410],
[-0.9137, 1.8242, -0.7872, -1.0762],
[-1.0629, -0.7037, -0.5402, -0.0247]],
[[-0.6074, 1.0865, 1.4428, 0.0430],
[ 0.8085, -1.8110, -0.4287, -1.1544],
[-1.4426, -1.9275, 1.1019, -0.3645]]]])
output_2d:tensor([[[[ 1.1819, 0.9983, 0.0450, -0.3839],
[-0.8228, 2.4024, -0.6739, -1.0143],
[-0.9987, -0.5755, -0.3829, 0.2244]],
[[-0.2974, 1.2006, 1.5157, 0.2778],
[ 0.9547, -1.3618, -0.1394, -0.7811],
[-1.0360, -1.4648, 1.2142, -0.0826]]]],
grad_fn=<NativeBatchNormBackward0>)
l1:tensor([[-0.9470, 0.6517, 0.1117, 0.3206],
[-1.2776, 0.7866, 0.5050, 0.1676]], grad_fn=<AddmmBackward0>)
output_1d:tensor([[ 0.9998, -0.9989, -0.9999, 0.9991],
[-0.9998, 0.9989, 0.9999, -0.9991]],
grad_fn=<NativeBatchNormBackward0>)
Process finished with exit code 0
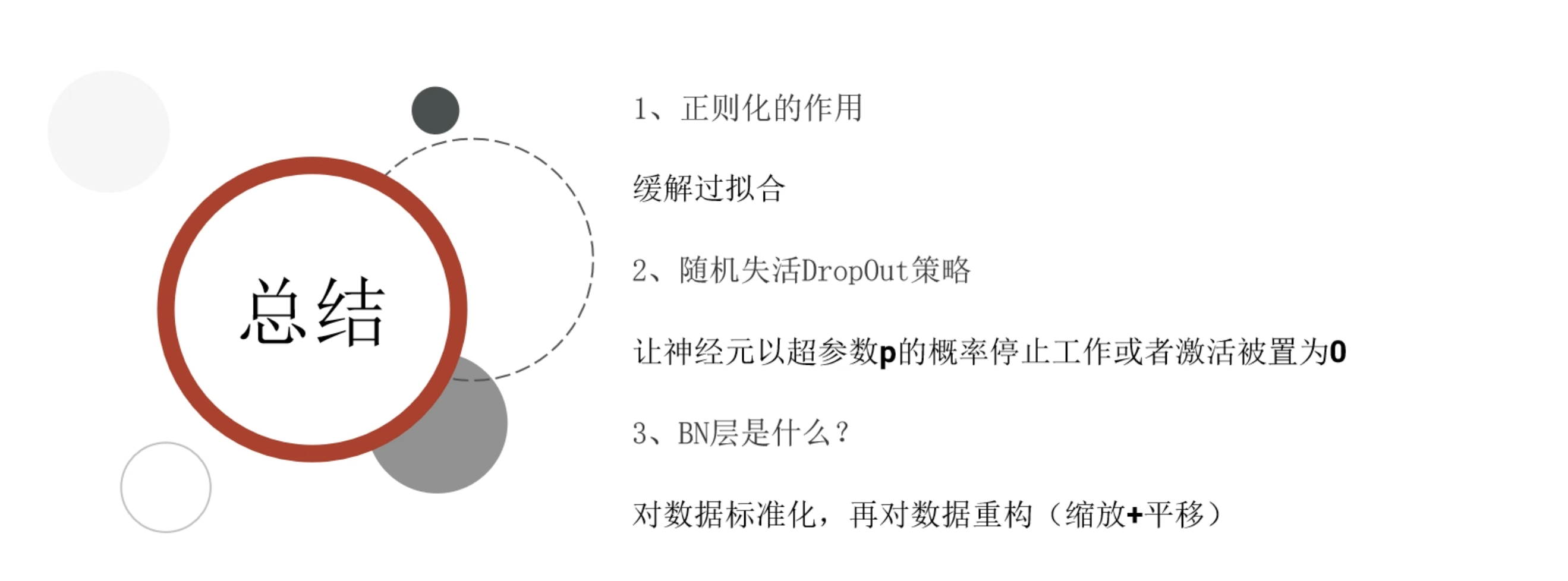
总结

























 3077
3077

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








