需求分析
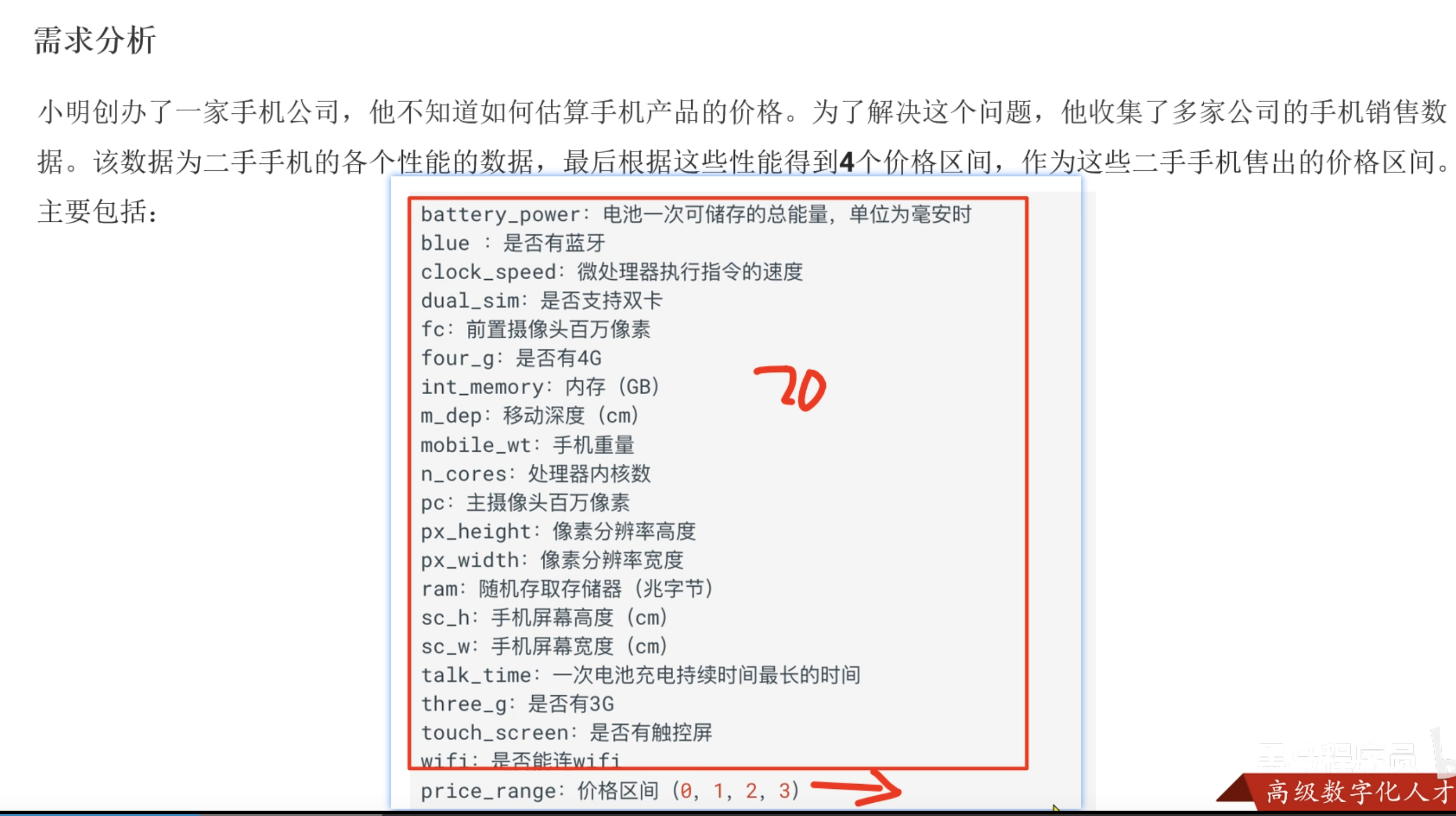
流程
准备训练集数据(要输出:训练数据集,测试数据集,输入特征数,输出特征数)
构建使用的模型
模型训练
模型评估

准备训练数据(五大步骤)
- 训练数据集(张量数据集 TensorDataset),测试数据集,输入特征数,输出特征数
- 步骤 1:读取表格数据(pandas)df = pd.read_csv("data.csv"),后的数据类型为DataFrame
- 步骤2:分离特征x,和标签y , 后的数据都是NumPy 数组(numpy.ndarray)类型。
- 步骤3:把 numpy 转成 Tensor :X_tensor = torch.tensor(X, dtype=torch.float32)
- 步骤4:打包为TensorDataset 张量数据集 (就是把输入和标签绑定成一个“样本单元”)也就是需要x,y进来两个张量
- 步骤5:放进 DataLoader(用于训练)数据加载器,可以将数据集分为一批一批数据 train_loader = DataLoader(dataset, batch_size=16, shuffle=True)
def create_dataset():
data = pd.read_csv('../data/手机价格预测.csv')
print(f'data:{data.head()}')
print(f'shape:{data.shape}')
# 分离出特征x 和标签y(也就是正确值)
x,y = data.iloc[:,:-1],data.iloc[:,-1]
x = x.astype(np.float32)
x_train, x_test, y_train, y_test = train_test_split(x,y, test_size=0.2, random_state=3, stratify=y)
# 数据转为张量数据集 TensorDataset 就是把输入和标签绑定成一个“样本单元”。
train_dataset = TensorDataset(torch.tensor(x_train.values), torch.tensor(y_train.values))
test_dataset = TensorDataset(torch.tensor(x_test.values), torch.tensor(y_test.values))
# 20也就是输入特征数 去重当做输出特征数
return train_dataset, test_dataset, x.shape[1], len(np.unique(y))
从表格数据到 DataLoader 的转换流程(最常用标准做法)
假设你有一份表格数据:CSV、Excel、numpy、pandas DataFrame 都可以。
我们以 pandas DataFrame 示例:
import pandas as pd
import torch
from torch.utils.data import TensorDataset, DataLoader
✅ 步骤 1:读取表格数据(pandas)
df = pd.read_csv("data.csv")
假设你的表格长这样:
|
feature1 |
feature2 |
feature3 |
label |
|
0.12 |
0.55 |
0.91 |
1 |
|
0.03 |
0.22 |
0.44 |
0 |
|
… |
… |
… |
… |
✅ 步骤 2:分离特征(X)和标签(y)
X = df[['feature1','feature2','feature3']].values
y = df['label'].values
X shape → (样本数, 特征数)
y shape → (样本数,)
✅ 步骤 3:把 numpy 转成 Tensor
X_tensor = torch.tensor(X, dtype=torch.float32)
y_tensor = torch.tensor(y, dtype=torch.long) # 分类任务用 long
✅ 步骤 4:打包成 TensorDataset
TensorDataset 就是把输入和标签绑定成一个“样本单元”。
dataset = TensorDataset(X_tensor, y_tensor)
每个样本结构变成:
dataset[i] = (X_tensor[i], y_tensor[i])
✅ 步骤 5:放进 DataLoader(用于训练)
train_loader = DataLoader(dataset, batch_size=16, shuffle=True)
DataLoader 负责:
- 每次自动给你 16 个样本
- 自动打乱(shuffle=True)
- 自动组合 batch
- 自动转成 GPU(你手动 .to(device))
🌟 完整流程图
表格数据 (CSV / Excel / DataFrame)
↓
DataFrame → numpy
↓
numpy → Tensor
↓
TensorDataset(X_tensor, y_tensor)
↓
DataLoader(dataset, batch_size=16, shuffle=True)
↓
for x_batch, y_batch in train_loader:
模型训练
构建使用的模型
- 三层模型 + relu
- 继承nn.Module
- def init(self,input_dim, output_dim): 初始化分类,搭建神经网络(隐藏层 + 输出层)
- def forward(self, x): 就是做完前向传播的完整链路,加权求和+激活函数 + 层层链接

class PhoneModel(nn.Module):
def __init__(self,input_dim, output_dim):
# 1.初始化分类
super().__init__()
# 2.搭建神经网络(隐藏层 + 输出层)
self.linear1 = nn.Linear(input_dim, 128)
self.linear2 = nn.Linear(128, 256)
self.output = nn.Linear(256, output_dim)
# 定义数据流动顺序(前向计算图)。完整的前向传播,加权求和 + 激活函数 + 层链接 + 输出
# self 代表 当前这个模型对象本身 self 就是 model
def forward(self, x):
# self.linear1(x) 就是在做 加权求和 + 加上 bias(偏置)
# torch.relu(...) 非线性激活
x = torch.relu(self.linear1(x))
x = torch.relu(self.linear2(x))
# 省略了softmax,因为我的
x = self.output(x)
# 返回模型最后的输出
return x
模型训练(4大步骤)
- 要先准备好3个东西: 定义好模型,定义好损失函数,定义好优化器
- 一轮训练:有反向传播(model.train())
- 一轮测试:没有反向传播(model.eval())
- 保存模型参数
准备3大东西
- 定义好模型(Model) model = PhoneModel(input_dim, output_dim)
- 定义好损失函数(Loss function) criterion = nn.CrossEntropyLoss()
- 定义好优化器(Optimizer) optimizer = optim.Adam(model.parameters(), lr=0.001)
训练
- 学习模型参数(权重、偏置等),让模型变好
- 训练集(有标签的样本)
- 前向传播 → 计算 loss → 反向传播 → 参数更新
测试
- 评估训练好的模型性能,看看效果怎么样
- 测试集(独立的,有标签或者无标签)
- 前向传播 → 计算指标(准确率、召回率等),无反向传播
保存模型(保存模型参数)
- 保存模型训练参数(权重和偏置)
torch.save(model.state_dict(), '../data/phone_model.pth')
|
方面 |
训练(Training) |
测试(Testing) |
|
目的 |
学习模型参数(权重、偏置等),让模型变好 |
评估训练好的模型性能,看看效果怎么样 |
|
数据 |
训练集(有标签的样本) |
测试集(独立的,有标签或者无标签) |
|
流程 |
前向传播 → 计算 loss → 反向传播 → 参数更新 |
前向传播 → 计算指标(准确率、召回率等),无反向传播 |
|
是否更新参数 |
会,不断调整权重 |
不更新参数,权重固定 |
|
是否计算梯度 |
是 |
否(通常关闭梯度计算,提高效率) |
|
代码区别 |
有 |
只有 |
训练流程model.train()(五步)
- ① 从 DataLoader 取一批数据(batch)
- ② 前向传播(forward)→ 得到预测值
- ③ 计算损失(loss)→ 看模型猜得多差
- ④ 反向传播(backward)→ 计算梯度
- ⑤ 优化器更新参数(optimizer.step())
① 从 DataLoader 取一批数据(batch)
x_batch, y_batch = next(DataLoader)
这一批数据例如 16 个样本:
x_batch:特征(输入)y_batch:标签(真实答案)
② 前向传播(forward)→ 得到预测值
y_pred = model(x_batch)
这一步做的是:
- 加权求和
- 激活函数
- 一层层运算
- 得到输出
也就是模型“猜测”答案。
③ 计算损失(loss)→ 看模型猜得多差
loss = criterion(y_pred, y_batch)
损失函数告诉你:
- 模型预测得准 → loss 小
- 模型预测得烂 → loss 大
④ 反向传播(backward)→ 计算梯度
loss.backward()
PyTorch 自动求导,得到:
- 每个权重应该往哪个方向动?
- 动多少?
这是神经网络的“学习”核心。
⑤ 优化器更新参数(optimizer.step())
optimizer.step()
optimizer.zero_grad()
优化器会:
- 根据梯度
- 更新模型的权重
- 让下一次预测更准
💡 训练循环整体长这样:
for epoch in range(epochs):
for x_batch, y_batch in train_loader:
y_pred = model(x_batch) # 1. forward
loss = criterion(y_pred, y_batch) # 2. loss
optimizer.zero_grad()
loss.backward() # 3. backward
optimizer.step() # 4. update
def train(tran_set, test_set, input_dim, output_dim, epochs):
# 参1:数据集对象(1600条数据), 参2:每批16条 参3:是否打乱数据
tran_loader = DataLoader(tran_set, batch_size=16, shuffle=True)
test_loader = DataLoader(test_set, batch_size=16, shuffle=True)
# 定义好模型
model = PhoneModel(input_dim, output_dim)
# 定义好损失函数
criterion = nn.CrossEntropyLoss()
# 定义好优化器
optimizer = optim.Adam(model.parameters(), lr=0.001)
train_losses = []
test_accuracies =[]
# 搭建训练循环
print("开始训练模型...")
for epoch in range(epochs):
model.train()
total_loss = 0
for x, y in tran_loader:
outputs = model(x)
loss = criterion(outputs, y)
optimizer.zero_grad()
loss.backward()
optimizer.step()
total_loss += loss.item()
# 每轮的平均损失
avg_loss = total_loss/len(tran_loader)
train_losses.append(avg_loss)
# 测试阶段
model.eval()
# 正确的个数
correct = 0
# 测试集样本总数
total = 0
# 关闭梯度计算(因为测试时不需要反向传播和梯度。)
with torch.no_grad():
for x, y in test_loader:
# 模型前向推理,前向传播
outputs = model(x)
# 取预测类别(argmax)
# dim = 0 → 按“列”取最大值
# dim = 1 → 按“行”取最大值(分类用这个)
'''
[2.1, -0.5, 1.8]
↑ ↑ ↑
类别0 类别1 类别2 的得分
torch.max(outputs, 1) 返回 values, indices = torch.max(outputs, 1)
它返回 两个东西:
values —— 每行的最大值
indices —— 每行最大值所在的下标(也就是预测的类别)
我只需要第二个值,把第一个值用 _ 忽略掉。
'''
_,predicted = torch.max(outputs, 1)
total += y.size(0)
correct += (predicted == y).sum().item()
test_acc = round(correct/ total * 100, 2)
test_accuracies.append(test_acc)
print(f'epoch:{epoch + 1}, avg_loss:{avg_loss:.4f} , TestAcc:{test_acc}%')
# 保存模型参数
torch.save(model.state_dict(), '../data/phone_model.pth')
print("模型已保存至 phone_model.pth")
# 绘制训练损失和测试准确率曲线
fig, axes = plt.subplots(1, 2, figsize=(12, 4))
axes[0].plot(train_losses, label='训练损失')
axes[0].set_xlabel('Epoch')
axes[0].set_ylabel('Loss')
axes[0].set_title('训练损失曲线')
axes[0].legend()
axes[0].grid(True)
axes[1].plot(test_accuracies, label='测试准确率', color='orange')
axes[1].set_xlabel('Epoch')
axes[1].set_ylabel('Accuracy (%)')
axes[1].set_title('测试准确率曲线')
axes[1].legend()
axes[1].grid(True)
plt.tight_layout()
plt.show()
return model
模型评估
- 准备数据 + 加载模型 + 用模型预测数据 + 计算评价指标
很好的问题!训练和测试阶段确实都会用到计算指标,但它们的侧重点和用途有所不同:
训练阶段的指标计算和测试评估阶段的指标计算的区别
训练阶段的指标计算
- 主要目的是监控训练过程,判断模型是否在学习、是否过拟合或欠拟合。
- 通常计算损失(loss),以及有时会计算**准确率(accuracy)**等辅助指标。
- 这些指标用于指导是否调整学习率、修改网络结构、提前停止等。
测试(评估)阶段的指标计算
- 重点是评估模型的最终泛化能力,即模型对“新数据”的表现。
- 在完全没参与训练的数据上计算指标,保证客观公正。
- 计算更全面的指标,如准确率(accuracy)、精确率(precision)、召回率(recall)、F1-score 等,以全面衡量模型性能。
- 这些指标决定模型是否达到上线标准,或者比较不同模型优劣。
总结
- 训练时用准确率监控,发现准确率一直不升,说明模型可能没学好。
- 训练结束后,用测试集算准确率和 F1-score,决定模型是否能上线。
|
阶段 |
指标作用 |
典型指标 |
|
训练阶段 |
监控训练进展、调参辅助 |
Loss、Accuracy(偶尔) |
|
测试/评估阶段 |
最终性能验证,模型质量评判 |
Accuracy、Precision、Recall、F1-score 等 |
测试代码
import torch
from torch.utils.data import Dataset, DataLoader, TensorDataset
import torch.nn as nn
import torch.optim as optim
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import time
from torchsummary import summary
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei'] # 指定默认字体为黑体
plt.rcParams['axes.unicode_minus'] = False # 解决负号 '-' 显示为方块的问题
def create_dataset():
data = pd.read_csv('../data/手机价格预测.csv')
print(f'data:{data.head()}')
print(f'shape:{data.shape}')
# 分离出特征x 和标签y(也就是正确值)
x,y = data.iloc[:,:-1],data.iloc[:,-1]
x = x.astype(np.float32)
x_train, x_test, y_train, y_test = train_test_split(x,y, test_size=0.2, random_state=3, stratify=y)
# 数据转为张量数据集 TensorDataset 就是把输入和标签绑定成一个“样本单元”。
train_dataset = TensorDataset(torch.tensor(x_train.values), torch.tensor(y_train.values))
test_dataset = TensorDataset(torch.tensor(x_test.values), torch.tensor(y_test.values))
# 20也就是输入特征数 去重当做输出特征数
return train_dataset, test_dataset, x.shape[1], len(np.unique(y))
pass
class PhoneModel(nn.Module):
def __init__(self,input_dim, output_dim):
# 1.初始化分类
super().__init__()
# 2.搭建神经网络(隐藏层 + 输出层)
self.linear1 = nn.Linear(input_dim, 128)
self.linear2 = nn.Linear(128, 256)
self.output = nn.Linear(256, output_dim)
# 定义数据流动顺序(前向计算图)。完整的前向传播,加权求和 + 激活函数 + 层链接 + 输出
# self 代表 当前这个模型对象本身 self 就是 model
def forward(self, x):
# self.linear1(x) 就是在做 加权求和 + 加上 bias(偏置)
# torch.relu(...) 非线性激活
x = torch.relu(self.linear1(x))
x = torch.relu(self.linear2(x))
# 省略了softmax,因为我的
x = self.output(x)
# 返回模型最后的输出
return x
def train(tran_set, test_set, input_dim, output_dim, epochs):
# 参1:数据集对象(1600条数据), 参2:每批16条 参3:是否打乱数据
tran_loader = DataLoader(tran_set, batch_size=16, shuffle=True)
test_loader = DataLoader(test_set, batch_size=16, shuffle=True)
# 定义好模型
model = PhoneModel(input_dim, output_dim)
# 定义好损失函数
criterion = nn.CrossEntropyLoss()
# 定义好优化器
optimizer = optim.Adam(model.parameters(), lr=0.001)
train_losses = []
test_accuracies =[]
# 搭建训练循环
print("开始训练模型...")
for epoch in range(epochs):
model.train()
total_loss = 0
for x, y in tran_loader:
outputs = model(x)
loss = criterion(outputs, y)
optimizer.zero_grad()
loss.backward()
optimizer.step()
total_loss += loss.item()
# 每轮的平均损失
avg_loss = total_loss/len(tran_loader)
train_losses.append(avg_loss)
# 测试阶段
model.eval()
# 正确的个数
correct = 0
# 测试集样本总数
total = 0
# 关闭梯度计算(因为测试时不需要反向传播和梯度。)
with torch.no_grad():
for x, y in test_loader:
# 模型前向推理,前向传播
outputs = model(x)
# 取预测类别(argmax)
# dim = 0 → 按“列”取最大值
# dim = 1 → 按“行”取最大值(分类用这个)
'''
[2.1, -0.5, 1.8]
↑ ↑ ↑
类别0 类别1 类别2 的得分
torch.max(outputs, 1) 返回 values, indices = torch.max(outputs, 1)
它返回 两个东西:
values —— 每行的最大值
indices —— 每行最大值所在的下标(也就是预测的类别)
我只需要第二个值,把第一个值用 _ 忽略掉。
'''
_,predicted = torch.max(outputs, 1)
total += y.size(0)
correct += (predicted == y).sum().item()
test_acc = round(correct/ total * 100, 2)
test_accuracies.append(test_acc)
print(f'epoch:{epoch + 1}, avg_loss:{avg_loss:.4f} , TestAcc:{test_acc}%')
# 保存模型参数
torch.save(model.state_dict(), '../data/phone_model.pth')
print("模型已保存至 phone_model.pth")
# 绘制训练损失和测试准确率曲线
fig, axes = plt.subplots(1, 2, figsize=(12, 4))
axes[0].plot(train_losses, label='训练损失')
axes[0].set_xlabel('Epoch')
axes[0].set_ylabel('Loss')
axes[0].set_title('训练损失曲线')
axes[0].legend()
axes[0].grid(True)
axes[1].plot(test_accuracies, label='测试准确率', color='orange')
axes[1].set_xlabel('Epoch')
axes[1].set_ylabel('Accuracy (%)')
axes[1].set_title('测试准确率曲线')
axes[1].legend()
axes[1].grid(True)
plt.tight_layout()
plt.show()
return model
def load_and_test(input_dim, output_dim):
model = PhoneModel(input_dim, output_dim)
model.load_state_dict(torch.load('../data/phone_model.pth'))
# 随机生成一条输入数据,假设输入特征是20维(生成符合标准正态分布(均值0,标准差1)的随机数)
'''
标准正态分布的定义
标准正态分布 是正态分布的一种特殊情况。
它的 均值(Mean)是 0,表示数据的平均值集中在 0。
它的 标准差(Standard Deviation)是 1,表示数据的离散程度(波动范围)大小为1。
具体含义
均值 0:数据“中心”在 0 附近。
标准差 1:大部分数据点(约68%)会落在均值的正负 1 个标准差范围内,也就是 [−1,1]。
99.7% 的数据点 会落在均值正负3个标准差范围内,也就是 [−3,3]。
'''
# example_features = np.random.randn(1, 20).astype(np.float32)
# input_tensor = torch.tensor(example_features)
# # 预测时模型切换到eval模式
# model.eval()
#
# with torch.no_grad():
# outputs = model(input_tensor)
# _, predicted = torch.max(outputs, 1)
#
# print(f"预测类别索引: {predicted.item()}")
# 这里演示一个简单的推断例子(假设用部分测试集数据)
# 真实使用时可以用更全面的测试流程
data = pd.read_csv('../data/手机价格预测.csv')
x, y = data.iloc[:, :-1], data.iloc[:, -1]
x = x.astype(np.float32)
x_test = torch.tensor(x.values)
with torch.no_grad():
outputs = model(x_test)
_, predicted = torch.max(outputs, 1)
y_true = y.values # 真实标签
y_pred = predicted.numpy() # 预测标签 转成 numpy 数组
# 计算指标
accuracy = accuracy_score(y_true, y_pred)
precision = precision_score(y_true, y_pred, average='weighted') # 多分类加权平均
recall = recall_score(y_true, y_pred, average='weighted')
f1 = f1_score(y_true, y_pred, average='weighted')
print("真实类别前10条:", y_true[:10].tolist())
print("预测类别前10条:", y_pred[:10].tolist())
print(f"准确率 (Accuracy): {accuracy:.4f}")
print(f"精确率 (Precision): {precision:.4f}")
print(f"召回率 (Recall): {recall:.4f}")
print(f"F1-score: {f1:.4f}")
if __name__ == '__main__':
train_dataset, test_dataset, input_dim, output_dim = create_dataset()
print(f'input_dim:{input_dim}')
print(f'output_dim:{output_dim}')
train(train_dataset, test_dataset,input_dim, output_dim, 50)
load_and_test(input_dim, output_dim)
测试结果
D:\pythonDemo\.venv\Scripts\python.exe -X pycache_prefix=C:\Users\Administrator.SY-202408261506\AppData\Local\JetBrains\PyCharm2025.3\cpython-cache "D:/Software/PyCharm 2025.3/plugins/python-ce/helpers/pydev/pydevd.py" --multiprocess --qt-support=auto --client 127.0.0.1 --port 49474 --file D:\pythonDemo\demo\test27_ann_phone.py
Connected to: <socket.socket fd=640, family=2, type=1, proto=0, laddr=('127.0.0.1', 49475), raddr=('127.0.0.1', 49474)>.
Connected to pydev debugger (build 253.28294.336)
data: battery_power blue clock_speed ... touch_screen wifi price_range
0 842 0 2.2 ... 0 1 1
1 1021 1 0.5 ... 1 0 2
2 563 1 0.5 ... 1 0 2
3 615 1 2.5 ... 0 0 2
4 1821 1 1.2 ... 1 0 1
[5 rows x 21 columns]
shape:(2000, 21)
input_dim:20
output_dim:4
开始训练模型...
epoch:1, avg_loss:12.2327 , TestAcc:52.5%
epoch:2, avg_loss:4.3582 , TestAcc:53.25%
epoch:3, avg_loss:3.9157 , TestAcc:43.75%
epoch:4, avg_loss:4.1651 , TestAcc:50.75%
epoch:5, avg_loss:2.2672 , TestAcc:61.75%
epoch:6, avg_loss:2.9912 , TestAcc:63.25%
epoch:7, avg_loss:1.4561 , TestAcc:55.75%
epoch:8, avg_loss:1.7498 , TestAcc:61.0%
epoch:9, avg_loss:1.2462 , TestAcc:54.25%
epoch:10, avg_loss:1.4452 , TestAcc:63.25%
epoch:11, avg_loss:1.5497 , TestAcc:61.75%
epoch:12, avg_loss:1.2456 , TestAcc:59.5%
epoch:13, avg_loss:1.0575 , TestAcc:62.0%
epoch:14, avg_loss:1.1040 , TestAcc:55.0%
epoch:15, avg_loss:0.9138 , TestAcc:67.25%
epoch:16, avg_loss:1.0124 , TestAcc:62.75%
epoch:17, avg_loss:0.8014 , TestAcc:62.0%
epoch:18, avg_loss:0.8998 , TestAcc:61.25%
epoch:19, avg_loss:0.7951 , TestAcc:65.5%
epoch:20, avg_loss:0.7324 , TestAcc:69.75%
epoch:21, avg_loss:0.7742 , TestAcc:59.75%
epoch:22, avg_loss:0.9613 , TestAcc:65.5%
epoch:23, avg_loss:0.8440 , TestAcc:65.75%
epoch:24, avg_loss:0.7014 , TestAcc:69.5%
epoch:25, avg_loss:0.6506 , TestAcc:69.75%
epoch:26, avg_loss:0.6491 , TestAcc:67.0%
epoch:27, avg_loss:0.6374 , TestAcc:64.0%
epoch:28, avg_loss:0.6607 , TestAcc:70.0%
epoch:29, avg_loss:0.6015 , TestAcc:68.25%
epoch:30, avg_loss:0.6006 , TestAcc:64.75%
epoch:31, avg_loss:0.6279 , TestAcc:66.25%
epoch:32, avg_loss:0.6112 , TestAcc:69.5%
epoch:33, avg_loss:0.5953 , TestAcc:69.25%
epoch:34, avg_loss:0.6595 , TestAcc:68.0%
epoch:35, avg_loss:0.5924 , TestAcc:69.0%
epoch:36, avg_loss:0.5862 , TestAcc:67.75%
epoch:37, avg_loss:0.6022 , TestAcc:71.75%
epoch:38, avg_loss:0.5764 , TestAcc:73.25%
epoch:39, avg_loss:0.5912 , TestAcc:68.5%
epoch:40, avg_loss:0.5842 , TestAcc:73.0%
epoch:41, avg_loss:0.5790 , TestAcc:67.0%
epoch:42, avg_loss:0.5730 , TestAcc:73.75%
epoch:43, avg_loss:0.5526 , TestAcc:70.5%
epoch:44, avg_loss:0.5549 , TestAcc:73.0%
epoch:45, avg_loss:0.5977 , TestAcc:68.25%
epoch:46, avg_loss:0.5707 , TestAcc:71.5%
epoch:47, avg_loss:0.5528 , TestAcc:70.5%
epoch:48, avg_loss:0.5511 , TestAcc:66.0%
epoch:49, avg_loss:0.5648 , TestAcc:67.5%
epoch:50, avg_loss:0.6017 , TestAcc:70.25%
模型已保存至 phone_model.pth
真实类别前10条: [1, 2, 2, 2, 1, 1, 3, 0, 0, 0]
预测类别前10条: [1, 1, 2, 2, 1, 1, 2, 0, 0, 0]
准确率 (Accuracy): 0.7260
精确率 (Precision): 0.7391
召回率 (Recall): 0.7260
F1-score: 0.7276
Process finished with exit code 0
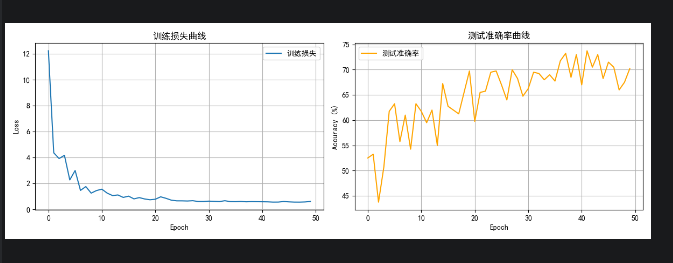
优化模型,优化思路
- 优化器优化,梯度下降从SGD优化为Adam
- 数据集进行标准化
- 增加网络深度,每层的神经元个数
- 增加训练轮数等等
- 更换其他激活函数等(LeakyReLU,避免“死神经元”问题 GELU,近年效果不错的激活函数
- 给各层加入随机失活,防止过拟合 x = self.dropout(x)

优化后的代码
import torch
from sklearn.preprocessing import StandardScaler
from torch.utils.data import Dataset, DataLoader, TensorDataset
import torch.nn as nn
import torch.optim as optim
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import time
from torchsummary import summary
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei'] # 指定默认字体为黑体
plt.rcParams['axes.unicode_minus'] = False # 解决负号 '-' 显示为方块的问题
def create_dataset():
data = pd.read_csv('../data/手机价格预测.csv')
print(f'data:{data.head()}')
print(f'shape:{data.shape}')
# 分离出特征x 和标签y(也就是正确值)
x,y = data.iloc[:,:-1],data.iloc[:,-1]
x = x.astype(np.float32)
x_train, x_test, y_train, y_test = train_test_split(x,y, test_size=0.2, random_state=3, stratify=y)
# 优化1、对数据进行标准化(这两个方法返回的是 numpy ndarray)
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)
# 数据转为张量数据集 TensorDataset 就是把输入和标签绑定成一个“样本单元”。
train_dataset = TensorDataset(torch.tensor(x_train), torch.tensor(y_train.values))
test_dataset = TensorDataset(torch.tensor(x_test), torch.tensor(y_test.values))
# train_dataset = TensorDataset(torch.tensor(x_train.values), torch.tensor(y_train.values))
# test_dataset = TensorDataset(torch.tensor(x_test.values), torch.tensor(y_test.values))
# 20也就是输入特征数 去重当做输出特征数
return train_dataset, test_dataset, x.shape[1], len(np.unique(y))
pass
class PhoneModel(nn.Module):
def __init__(self,input_dim, output_dim):
# 1.初始化分类
super().__init__()
# 优化2、增加网络层数和每层的神经元个数
# 2.搭建神经网络(隐藏层 + 输出层)
self.linear1 = nn.Linear(input_dim, 128)
self.linear2 = nn.Linear(128, 256)
self.linear3 = nn.Linear(256, 512)
self.linear4 = nn.Linear(512, 256)
self.output = nn.Linear(256, output_dim)
self.dropout = nn.Dropout(p=0.3)
# 定义数据流动顺序(前向计算图)。完整的前向传播,加权求和 + 激活函数 + 层链接 + 输出
# self 代表 当前这个模型对象本身 self 就是 model
def forward(self, x):
# self.linear1(x) 就是在做 加权求和 + 加上 bias(偏置)
# torch.relu(...) 非线性激活
x = torch.relu(self.linear1(x))
x = self.dropout(x) # 优化4、加入随机失活
x = torch.relu(self.linear2(x))
x = self.dropout(x)
x = torch.relu(self.linear3(x))
x = self.dropout(x)
x = torch.relu(self.linear4(x))
x = self.dropout(x)
# 省略了softmax,因为我的
x = self.output(x)
# 返回模型最后的输出
return x
def train(tran_set, test_set, input_dim, output_dim, epochs):
# 参1:数据集对象(1600条数据), 参2:每批16条 参3:是否打乱数据
tran_loader = DataLoader(tran_set, batch_size=16, shuffle=True)
test_loader = DataLoader(test_set, batch_size=16, shuffle=True)
# 定义好模型
model = PhoneModel(input_dim, output_dim)
# 定义好损失函数
criterion = nn.CrossEntropyLoss()
# 定义好优化器(SGD 是最基础的梯度下降算法,随机梯度下降),优化6、选择更好的梯度下降
optimizer = optim.Adam(model.parameters(), lr=0.001)
train_losses = []
test_accuracies =[]
# 搭建训练循环
print("开始训练模型...")
for epoch in range(epochs):
model.train()
total_loss = 0
for x, y in tran_loader:
outputs = model(x)
loss = criterion(outputs, y)
optimizer.zero_grad()
loss.backward()
optimizer.step()
total_loss += loss.item()
# 每轮的平均损失
avg_loss = total_loss/len(tran_loader)
train_losses.append(avg_loss)
# 测试阶段
model.eval()
# 正确的个数
correct = 0
# 测试集样本总数
total = 0
# 关闭梯度计算(因为测试时不需要反向传播和梯度。)
with torch.no_grad():
for x, y in test_loader:
# 模型前向推理,前向传播
outputs = model(x)
# 取预测类别(argmax)
# dim = 0 → 按“列”取最大值
# dim = 1 → 按“行”取最大值(分类用这个)
'''
[2.1, -0.5, 1.8]
↑ ↑ ↑
类别0 类别1 类别2 的得分
torch.max(outputs, 1) 返回 values, indices = torch.max(outputs, 1)
它返回 两个东西:
values —— 每行的最大值
indices —— 每行最大值所在的下标(也就是预测的类别)
我只需要第二个值,把第一个值用 _ 忽略掉。
'''
_,predicted = torch.max(outputs, 1)
total += y.size(0)
correct += (predicted == y).sum().item()
test_acc = round(correct/ total * 100, 2)
test_accuracies.append(test_acc)
print(f'epoch:{epoch + 1}, avg_loss:{avg_loss:.4f} , TestAcc:{test_acc}%')
# 保存模型参数
torch.save(model.state_dict(), '../data/phone_model.pth')
print("模型已保存至 phone_model.pth")
# 绘制训练损失和测试准确率曲线
fig, axes = plt.subplots(1, 2, figsize=(12, 4))
axes[0].plot(train_losses, label='训练损失')
axes[0].set_xlabel('Epoch')
axes[0].set_ylabel('Loss')
axes[0].set_title('训练损失曲线')
axes[0].legend()
axes[0].grid(True)
axes[1].plot(test_accuracies, label='测试准确率', color='orange')
axes[1].set_xlabel('Epoch')
axes[1].set_ylabel('Accuracy (%)')
axes[1].set_title('测试准确率曲线')
axes[1].legend()
axes[1].grid(True)
plt.tight_layout()
plt.show()
return model
def load_and_test(input_dim, output_dim):
model = PhoneModel(input_dim, output_dim)
model.load_state_dict(torch.load('../data/phone_model.pth'))
# 随机生成一条输入数据,假设输入特征是20维(生成符合标准正态分布(均值0,标准差1)的随机数)
'''
标准正态分布的定义
标准正态分布 是正态分布的一种特殊情况。
它的 均值(Mean)是 0,表示数据的平均值集中在 0。
它的 标准差(Standard Deviation)是 1,表示数据的离散程度(波动范围)大小为1。
具体含义
均值 0:数据“中心”在 0 附近。
标准差 1:大部分数据点(约68%)会落在均值的正负 1 个标准差范围内,也就是 [−1,1]。
99.7% 的数据点 会落在均值正负3个标准差范围内,也就是 [−3,3]。
'''
# example_features = np.random.randn(1, 20).astype(np.float32)
# input_tensor = torch.tensor(example_features)
# # 预测时模型切换到eval模式
# model.eval()
#
# with torch.no_grad():
# outputs = model(input_tensor)
# _, predicted = torch.max(outputs, 1)
#
# print(f"预测类别索引: {predicted.item()}")
# 这里演示一个简单的推断例子(假设用部分测试集数据)
# 真实使用时可以用更全面的测试流程
data = pd.read_csv('../data/手机价格预测.csv')
x, y = data.iloc[:, :-1], data.iloc[:, -1]
x = x.astype(np.float32)
x_test = torch.tensor(x.values)
with torch.no_grad():
outputs = model(x_test)
_, predicted = torch.max(outputs, 1)
y_true = y.values # 真实标签
y_pred = predicted.numpy() # 预测标签 转成 numpy 数组
# 计算指标
accuracy = accuracy_score(y_true, y_pred)
precision = precision_score(y_true, y_pred, average='weighted', zero_division=0)
recall = recall_score(y_true, y_pred, average='weighted')
f1 = f1_score(y_true, y_pred, average='weighted')
print("真实类别前10条:", y_true[:10].tolist())
print("预测类别前10条:", y_pred[:10].tolist())
print(f"准确率 (Accuracy): {accuracy:.4f}")
print(f"精确率 (Precision): {precision:.4f}")
print(f"召回率 (Recall): {recall:.4f}")
print(f"F1-score: {f1:.4f}")
if __name__ == '__main__':
train_dataset, test_dataset, input_dim, output_dim = create_dataset()
print(f'input_dim:{input_dim}')
print(f'output_dim:{output_dim}')
# 优化5、增加训练论数
train(train_dataset, test_dataset,input_dim, output_dim, 100)
load_and_test(input_dim, output_dim)
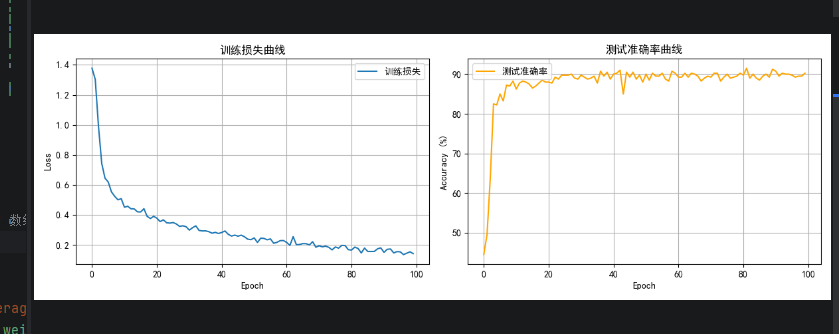
优化结果
- 从60% 优化为90%
D:\pythonDemo\.venv\Scripts\python.exe -X pycache_prefix=C:\Users\Administrator.SY-202408261506\AppData\Local\JetBrains\PyCharm2025.3\cpython-cache "D:/Software/PyCharm 2025.3/plugins/python-ce/helpers/pydev/pydevd.py" --multiprocess --qt-support=auto --client 127.0.0.1 --port 57256 --file D:\pythonDemo\demo\test27_ann_phone.py
Connected to: <socket.socket fd=600, family=2, type=1, proto=0, laddr=('127.0.0.1', 57257), raddr=('127.0.0.1', 57256)>.
Connected to pydev debugger (build 253.28294.336)
data: battery_power blue clock_speed ... touch_screen wifi price_range
0 842 0 2.2 ... 0 1 1
1 1021 1 0.5 ... 1 0 2
2 563 1 0.5 ... 1 0 2
3 615 1 2.5 ... 0 0 2
4 1821 1 1.2 ... 1 0 1
[5 rows x 21 columns]
shape:(2000, 21)
input_dim:20
output_dim:4
开始训练模型...
epoch:1, avg_loss:0.9702 , TestAcc:81.5%
epoch:2, avg_loss:0.5667 , TestAcc:83.75%
epoch:3, avg_loss:0.4718 , TestAcc:83.75%
epoch:4, avg_loss:0.4026 , TestAcc:86.25%
epoch:5, avg_loss:0.3480 , TestAcc:88.75%
epoch:6, avg_loss:0.3271 , TestAcc:86.75%
epoch:7, avg_loss:0.3070 , TestAcc:87.25%
epoch:8, avg_loss:0.3098 , TestAcc:88.75%
epoch:9, avg_loss:0.2432 , TestAcc:87.5%
epoch:10, avg_loss:0.2467 , TestAcc:89.25%
epoch:11, avg_loss:0.2253 , TestAcc:90.0%
epoch:12, avg_loss:0.2051 , TestAcc:91.0%
epoch:13, avg_loss:0.1940 , TestAcc:88.5%
epoch:14, avg_loss:0.2014 , TestAcc:88.25%
epoch:15, avg_loss:0.2007 , TestAcc:89.75%
epoch:16, avg_loss:0.1742 , TestAcc:90.0%
epoch:17, avg_loss:0.1852 , TestAcc:88.5%
epoch:18, avg_loss:0.1504 , TestAcc:88.25%
epoch:19, avg_loss:0.1566 , TestAcc:87.5%
epoch:20, avg_loss:0.1332 , TestAcc:89.5%
epoch:21, avg_loss:0.1477 , TestAcc:87.0%
epoch:22, avg_loss:0.1366 , TestAcc:89.5%
epoch:23, avg_loss:0.1180 , TestAcc:88.5%
epoch:24, avg_loss:0.1415 , TestAcc:88.25%
epoch:25, avg_loss:0.1329 , TestAcc:88.75%
epoch:26, avg_loss:0.1203 , TestAcc:89.25%
epoch:27, avg_loss:0.1119 , TestAcc:88.25%
epoch:28, avg_loss:0.1208 , TestAcc:89.25%
epoch:29, avg_loss:0.0995 , TestAcc:88.0%
epoch:30, avg_loss:0.1095 , TestAcc:89.0%
epoch:31, avg_loss:0.1024 , TestAcc:87.75%
epoch:32, avg_loss:0.1086 , TestAcc:89.5%
epoch:33, avg_loss:0.0917 , TestAcc:90.25%
epoch:34, avg_loss:0.0903 , TestAcc:89.25%
epoch:35, avg_loss:0.0790 , TestAcc:89.25%
epoch:36, avg_loss:0.0724 , TestAcc:88.5%
epoch:37, avg_loss:0.0950 , TestAcc:87.0%
epoch:38, avg_loss:0.0662 , TestAcc:89.75%
epoch:39, avg_loss:0.0701 , TestAcc:87.5%
epoch:40, avg_loss:0.0726 , TestAcc:89.25%
epoch:41, avg_loss:0.0816 , TestAcc:88.25%
epoch:42, avg_loss:0.0860 , TestAcc:90.5%
epoch:43, avg_loss:0.0672 , TestAcc:89.0%
epoch:44, avg_loss:0.0868 , TestAcc:90.0%
epoch:45, avg_loss:0.0786 , TestAcc:88.5%
epoch:46, avg_loss:0.0801 , TestAcc:90.25%
epoch:47, avg_loss:0.0645 , TestAcc:89.5%
epoch:48, avg_loss:0.0786 , TestAcc:88.75%
epoch:49, avg_loss:0.0580 , TestAcc:89.5%
epoch:50, avg_loss:0.0719 , TestAcc:90.5%
epoch:51, avg_loss:0.0674 , TestAcc:90.0%
epoch:52, avg_loss:0.0561 , TestAcc:89.75%
epoch:53, avg_loss:0.0798 , TestAcc:88.75%
epoch:54, avg_loss:0.0747 , TestAcc:90.0%
epoch:55, avg_loss:0.0708 , TestAcc:89.25%
epoch:56, avg_loss:0.0428 , TestAcc:87.25%
epoch:57, avg_loss:0.0697 , TestAcc:89.5%
epoch:58, avg_loss:0.0758 , TestAcc:90.0%
epoch:59, avg_loss:0.0379 , TestAcc:88.0%
epoch:60, avg_loss:0.0545 , TestAcc:89.0%
epoch:61, avg_loss:0.0581 , TestAcc:88.5%
epoch:62, avg_loss:0.0583 , TestAcc:88.75%
epoch:63, avg_loss:0.0519 , TestAcc:89.25%
epoch:64, avg_loss:0.0545 , TestAcc:89.0%
epoch:65, avg_loss:0.0853 , TestAcc:88.75%
epoch:66, avg_loss:0.0457 , TestAcc:89.25%
epoch:67, avg_loss:0.0663 , TestAcc:89.5%
epoch:68, avg_loss:0.0628 , TestAcc:88.25%
epoch:69, avg_loss:0.0709 , TestAcc:88.75%
epoch:70, avg_loss:0.0390 , TestAcc:88.25%
epoch:71, avg_loss:0.0450 , TestAcc:88.75%
epoch:72, avg_loss:0.0520 , TestAcc:89.0%
epoch:73, avg_loss:0.0343 , TestAcc:88.0%
epoch:74, avg_loss:0.0538 , TestAcc:88.75%
epoch:75, avg_loss:0.0653 , TestAcc:88.75%
epoch:76, avg_loss:0.0519 , TestAcc:86.75%
epoch:77, avg_loss:0.0438 , TestAcc:89.75%
epoch:78, avg_loss:0.0507 , TestAcc:88.75%
epoch:79, avg_loss:0.0453 , TestAcc:88.75%
epoch:80, avg_loss:0.0577 , TestAcc:89.25%
epoch:81, avg_loss:0.0279 , TestAcc:88.75%
epoch:82, avg_loss:0.0799 , TestAcc:87.25%
epoch:83, avg_loss:0.0479 , TestAcc:87.25%
epoch:84, avg_loss:0.0319 , TestAcc:89.75%
epoch:85, avg_loss:0.0536 , TestAcc:89.0%
epoch:86, avg_loss:0.0394 , TestAcc:90.25%
epoch:87, avg_loss:0.0396 , TestAcc:88.5%
epoch:88, avg_loss:0.0505 , TestAcc:86.75%
epoch:89, avg_loss:0.0479 , TestAcc:87.5%
epoch:90, avg_loss:0.0400 , TestAcc:88.25%
epoch:91, avg_loss:0.0500 , TestAcc:89.25%
epoch:92, avg_loss:0.0581 , TestAcc:90.75%
epoch:93, avg_loss:0.0442 , TestAcc:88.5%
epoch:94, avg_loss:0.0308 , TestAcc:90.0%
epoch:95, avg_loss:0.0431 , TestAcc:90.25%
epoch:96, avg_loss:0.0536 , TestAcc:89.75%
epoch:97, avg_loss:0.0451 , TestAcc:88.0%
epoch:98, avg_loss:0.0639 , TestAcc:89.5%
epoch:99, avg_loss:0.0395 , TestAcc:90.75%
epoch:100, avg_loss:0.0305 , TestAcc:88.5%
模型已保存至 phone_model.pth
真实类别前10条: [1, 2, 2, 2, 1, 1, 3, 0, 0, 0]
预测类别前10条: [3, 3, 3, 3, 3, 3, 3, 3, 3, 3]
准确率 (Accuracy): 0.2500
精确率 (Precision): 0.0625
召回率 (Recall): 0.2500
F1-score: 0.1000
Process finished with exit code 0
扩展知识点
1. 准确率 (Accuracy)
- 定义:模型预测正确的样本数占总样本数的比例。
- 计算公式:
- 解释:表示模型整体预测正确的能力。
- 你的结果: 0.7260,说明模型对全部测试样本中,有72.6%预测是正确的。
2. 精确率 (Precision)
- 定义:模型预测为某一类别的样本中,真正属于该类别的比例。
- 计算公式(针对某一类别):
- 解释:模型预测为正例时,有多少是准确的。
- 为什么重要:当误报代价大时(例如疾病诊断中的误诊),精确率是关键指标。
- 你的结果: 0.7391,说明模型预测为某个类别的样本中,约有73.91%是真正属于该类别的。
- 注意:你用的是多分类“加权平均”(weighted),考虑了各类别样本数量不同的影响。
3. 召回率 (Recall)
- 定义:真实属于某类别的样本中,被模型正确预测为该类别的比例。
- 计算公式(针对某一类别):
- 解释:模型对正例的“覆盖率”,能找到多少真正的正例。
- 为什么重要:当漏报代价大时(如安全漏洞检测),召回率很关键。
- 你的结果: 0.7260,说明模型能找回72.6%的真实正例。
4. F1-score
- 定义:精确率和召回率的调和平均数,是两者的折中指标。
- 计算公式:
- 解释:综合考虑了精确率和召回率,数值高说明模型整体表现均衡。
- 你的结果: 0.7276,说明模型在精确率和召回率之间达到了较好的平衡。
总结:
|
指标 |
反映的方面 |
高低代表 |
适用场景 |
|
准确率 |
整体预测正确率 |
高 = 好 |
样本均衡,无偏重类别 |
|
精确率 |
预测为正类的准确性 |
高 = 误报少 |
误报代价大时,如垃圾邮件检测 |
|
召回率 |
找出正类样本的能力 |
高 = 漏报少 |
漏报代价大时,如疾病筛查 |
|
F1-score |
精确率和召回率的平衡 |
高 = 综合性能好 |
两者同等重要时 |

4.精确率的简单案例说明
假设你做了一个二分类任务,目标是检测邮件是不是垃圾邮件。
|
邮件编号 |
真实标签(垃圾=1,正常=0) |
模型预测(垃圾=1,正常=0) |
|
1 |
1 |
1 |
|
2 |
0 |
1 |
|
3 |
1 |
1 |
|
4 |
0 |
0 |
|
5 |
1 |
0 |
先解释表格:
- 邮件1,真实是垃圾,模型预测也是垃圾 → 真正例 (TP)
- 邮件2,真实正常,模型预测成垃圾 → 假正例 (FP)
- 邮件3,真实垃圾,模型预测垃圾 → 真正例 (TP)
- 邮件4,真实正常,模型预测正常 → 真负例 (TN)
- 邮件5,真实垃圾,模型预测正常 → 假负例 (FN)
计算精确率:
- TP = 2(邮件1和邮件3)
- FP = 1(邮件2)
代入:
解释:
- 模型预测“垃圾邮件”的次数是 3 次(邮件1、邮件2、邮件3)
- 其中,有 2 次预测正确(邮件1和邮件3真的垃圾)
- 有 1 次预测错误(邮件2其实正常)
所以,精确率约为 66.67%,意味着:
当模型说“这是垃圾邮件”的时候,大约有 66.67% 的概率它说对了。
























 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








