zemax学习第三天

原创已于 2025-12-26 20:34:27 修改 · 941 阅读

15 ·

CC 4.0 BY-SA版权

文章标签：

#学习

于 2025-12-26 20:29:41 首次发布

zemax 专栏收录该内容

6 篇文章

订阅专栏

离轴三反光学系统

反射式光学系统具有无色差的特性，传统的同轴两反光学系统具有存在遮拦、视场小等问题，离轴三反系统有更多的优化变量，可以矫正全部的初级像差，可以实现无遮拦、大视场、大相对孔径、高成像质量、长焦距，但存在检测装备难。

指标要求

D:250mm
f:1000mm
视场-2°-2°，9°-11°
可见光

设计

使用ZEBASE库中的离轴三反结构O_015

进行缩放镜头：1.25，修改视场参数，可见光波段

去掉原初始孔径的预先设置值，并插入相应坐标间断面，使得后面对应的偏心和角度可以进行优化。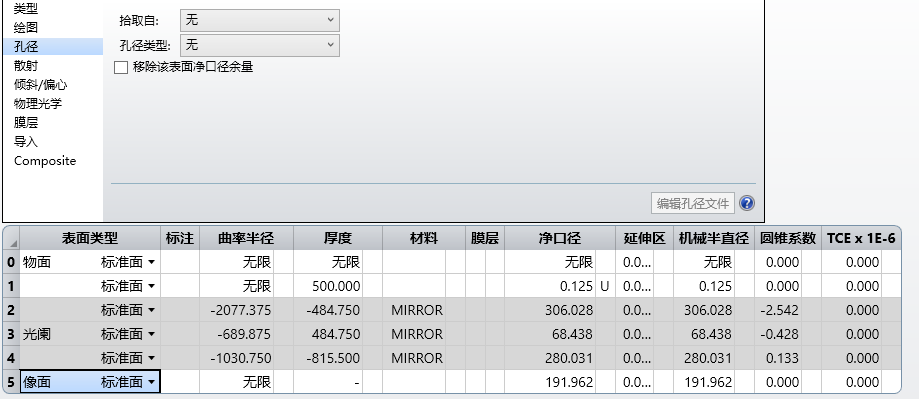

在每个反射面前加入坐标间断面并将像面改为倾斜面

如果一个反射镜将光线翻转180°，那么下一个面的位置应该在负Z方向，但如果没有坐标间断，厚度总是沿+Z方向测量，无法到达那里。

为什么需要两个坐标间断？

第一个坐标间断：将坐标系旋转，使反射镜的法线方向与新的Z轴一致
反射镜面：在旋转后的坐标系中，反射镜是“平面镜”或“球面镜”，沿新的Z轴放置
第二个坐标间断：将坐标系旋转回原方向（或转到下一个反射镜所需的方向）

优化

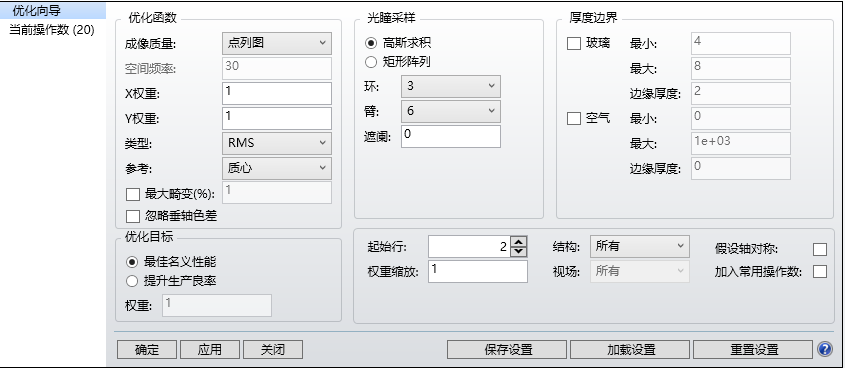
添加操作数

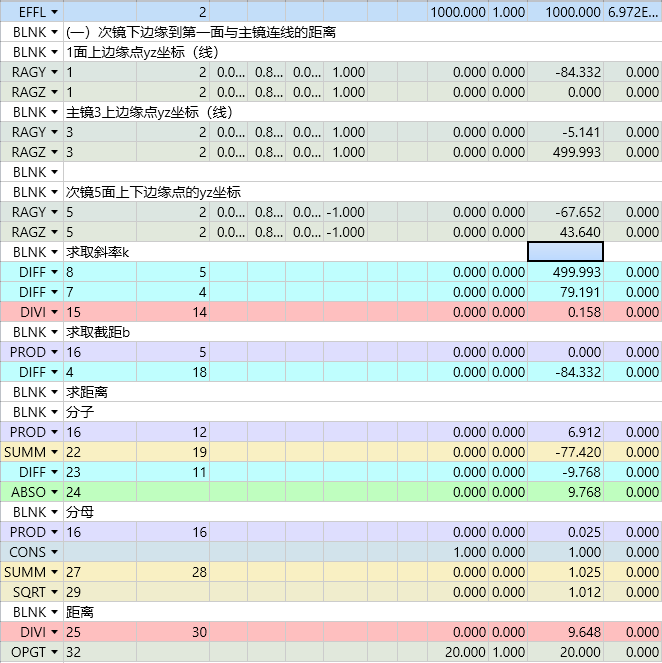
RAGY：追迹指定光线，获取其在面1上的Y坐标（归一化视场0.8，归一化孔径1.0，即上边缘点）。
- 结果：-95.217mm（说明有离轴）
RAGZ：获取同一光线在面1上的Z坐标。
- 结果：0.000mm（通常光轴方向为Z）
这些坐标用于后续的直线拟合。

计算直线斜率

DIFF 8-5：计算主镜与面1的 Z坐标差（ΔZ）。
DIFF 7-4：计算主镜与面1的 Y坐标差（ΔY）。
DIVI 15/14：计算斜率 k = ΔY/ΔZ ≈ -9.522×10⁻⁹（几乎为0，说明直线接近平行光轴）

计算截距

利用公式 b = Y₁ - k×Z₁，计算直线方程 Y = kZ + b 的截距b。
因为k≈0，b≈Y₁≈-95.217（但计算显示0.000，可能是当前迭代值）。

计算点到直线的距离

分子（操作数21-25）：
计算 |k×Z₂ + b - Y₂|（次镜边缘点到直线的垂直Y方向偏差）
分母（操作数26-30）：
计算 √(k² + 1)（直线斜率的归一化因子）
操作数32（DIVI 25/30）：
最终得到距离 d = |k×Z₂ + b - Y₂| / √(k² + 1)

确保次镜下边缘与物面-主镜上边缘连线之间的距离大于20mm，这是为了避免遮拦（vignetting） 或保证机械间隙。

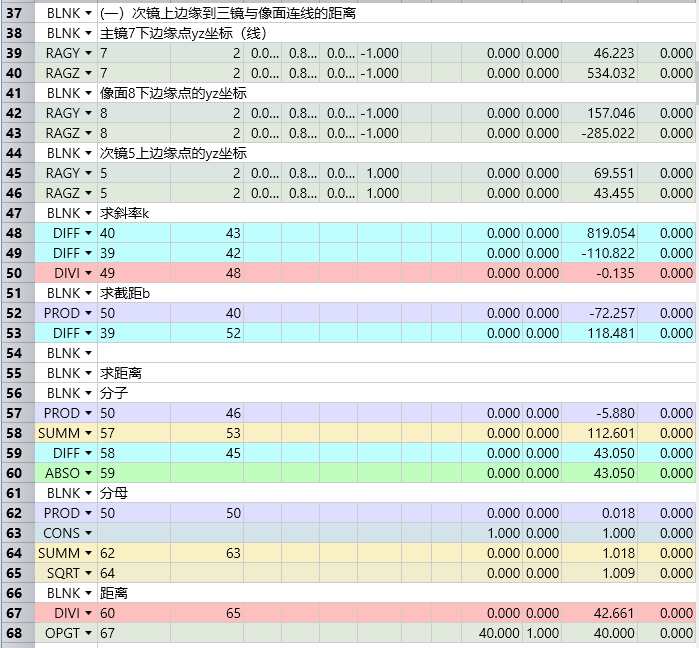
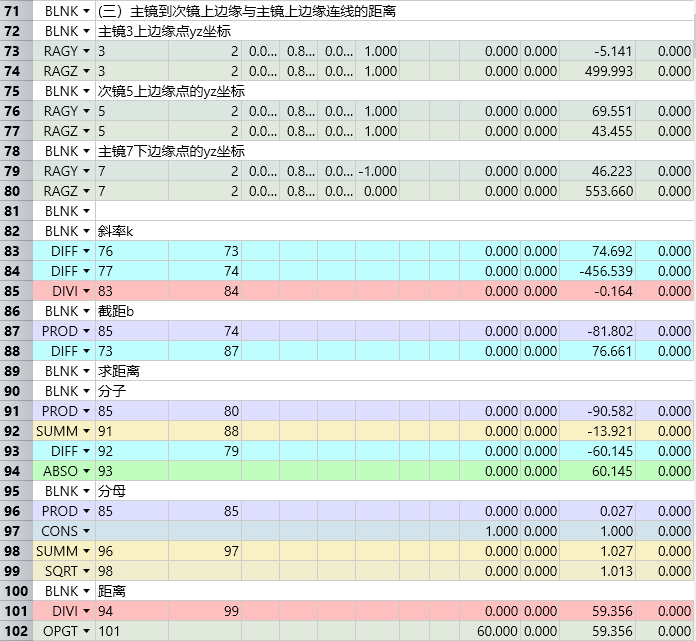
设置变量，进行优化

优化前

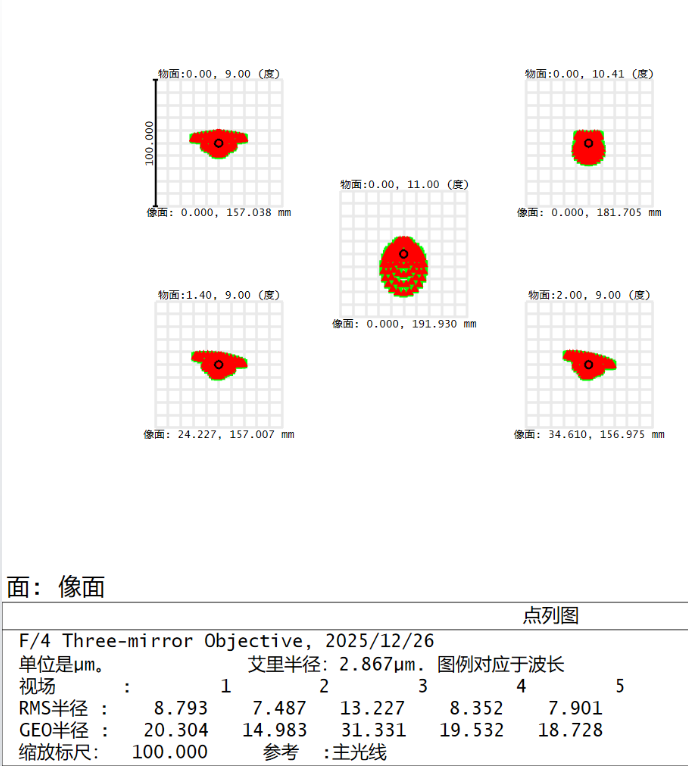
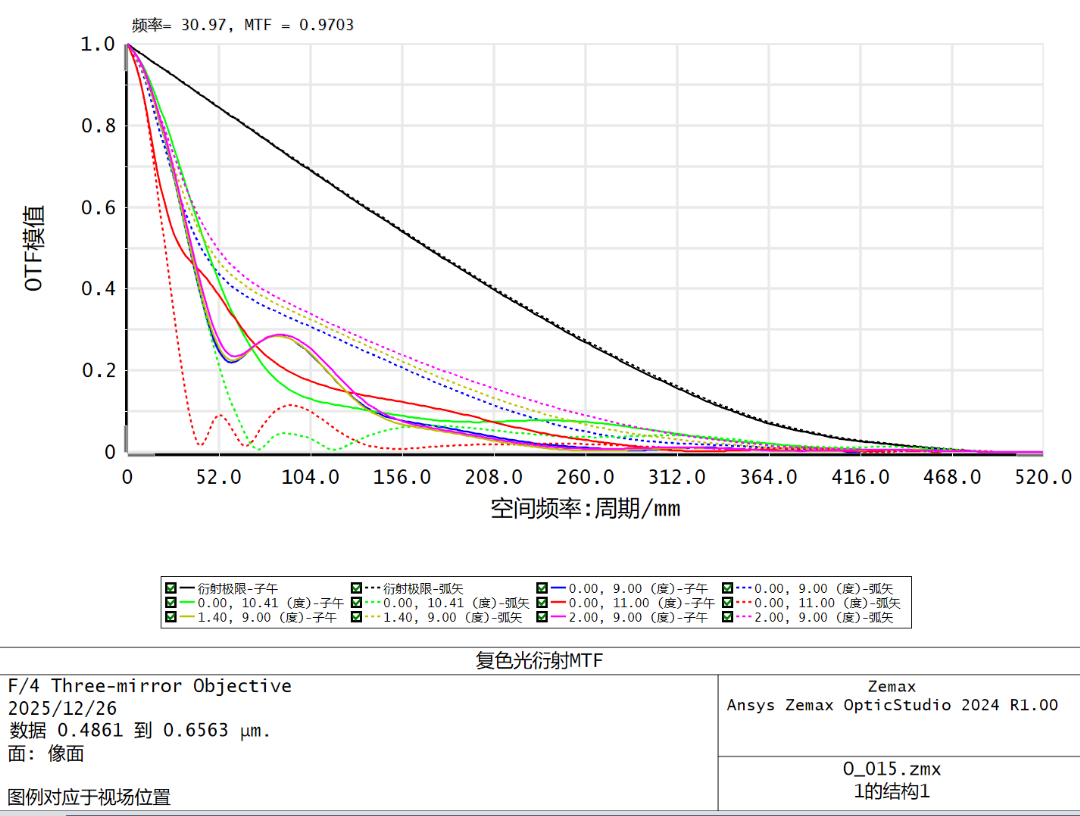
设置变量进行全局优化

优化结果

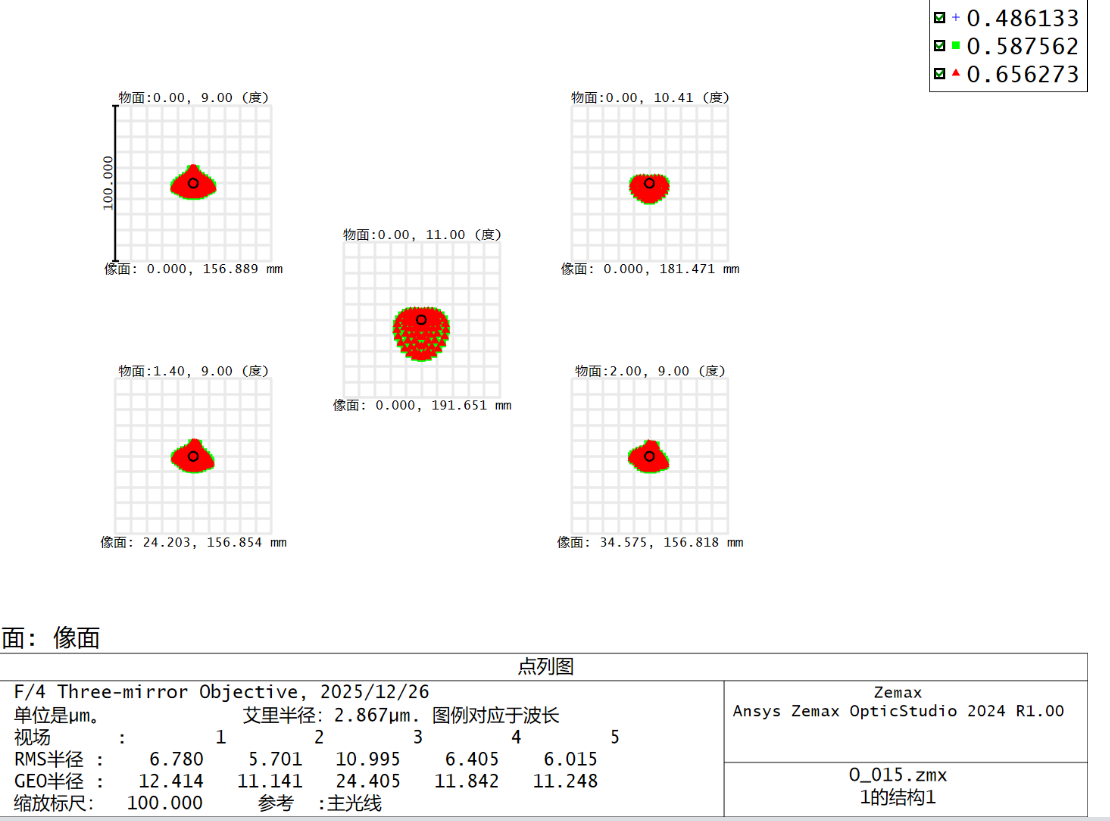
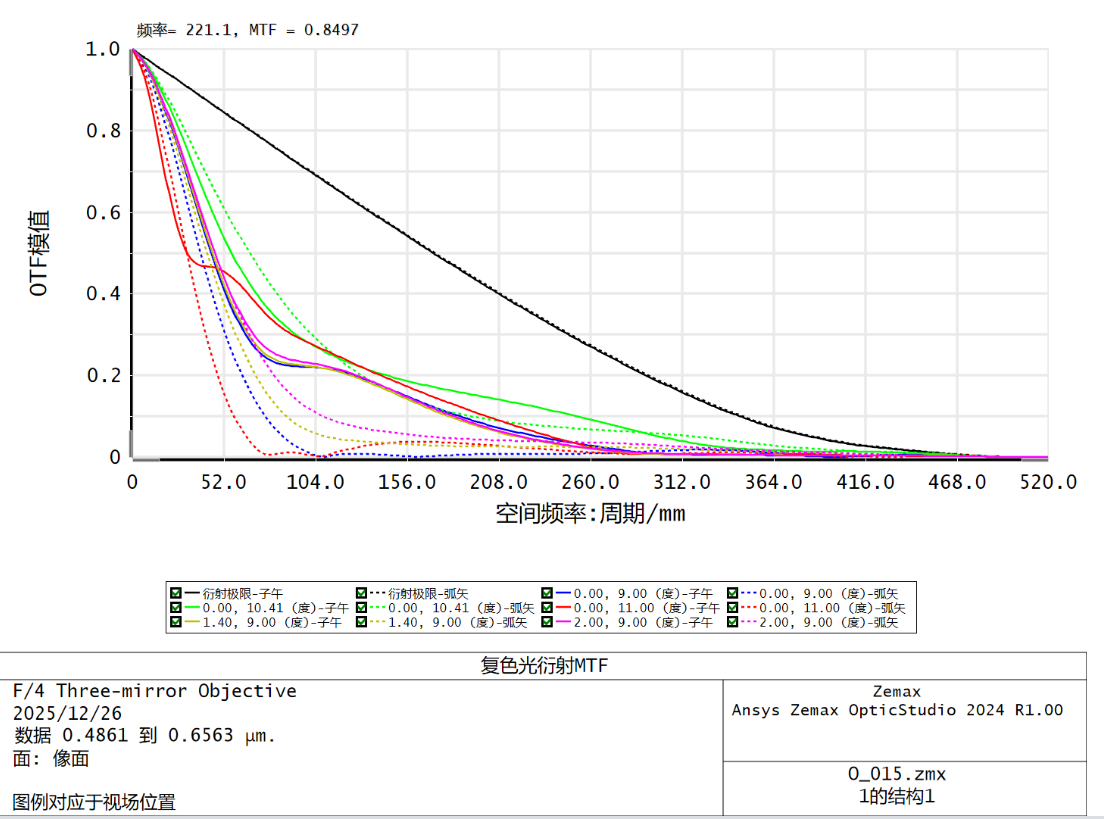
此时评价函数为0.004，评价函数小，优化效果不明显。

修改评价函数，改为对比度，进行优化，优化函数由0.1变为0.04

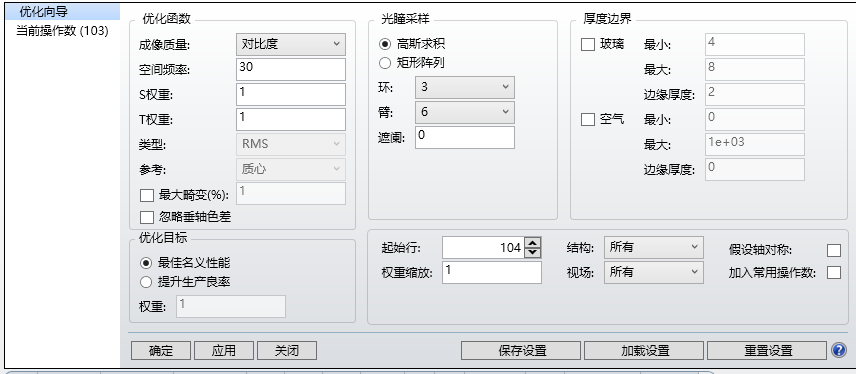
查看优化结构

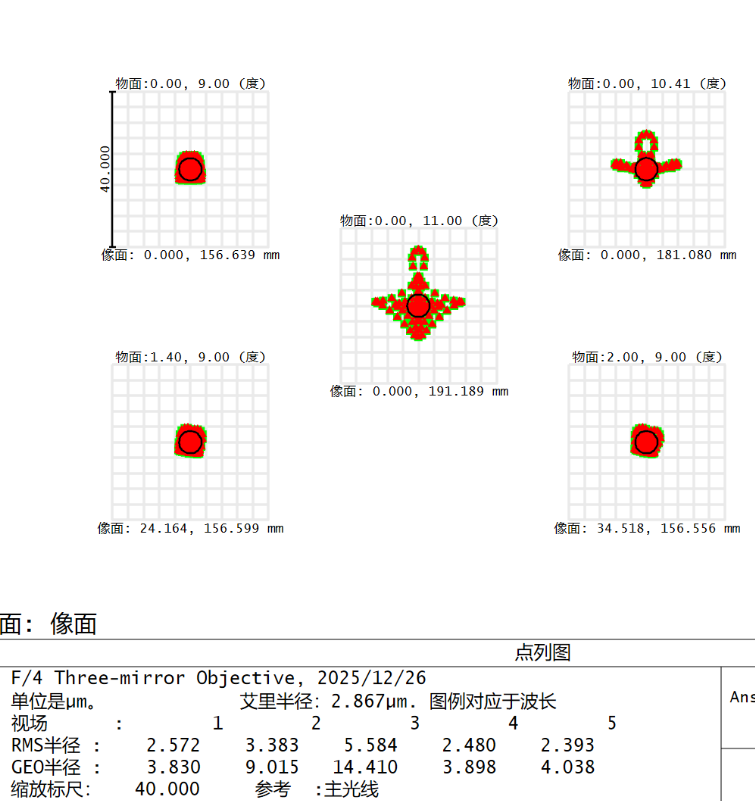
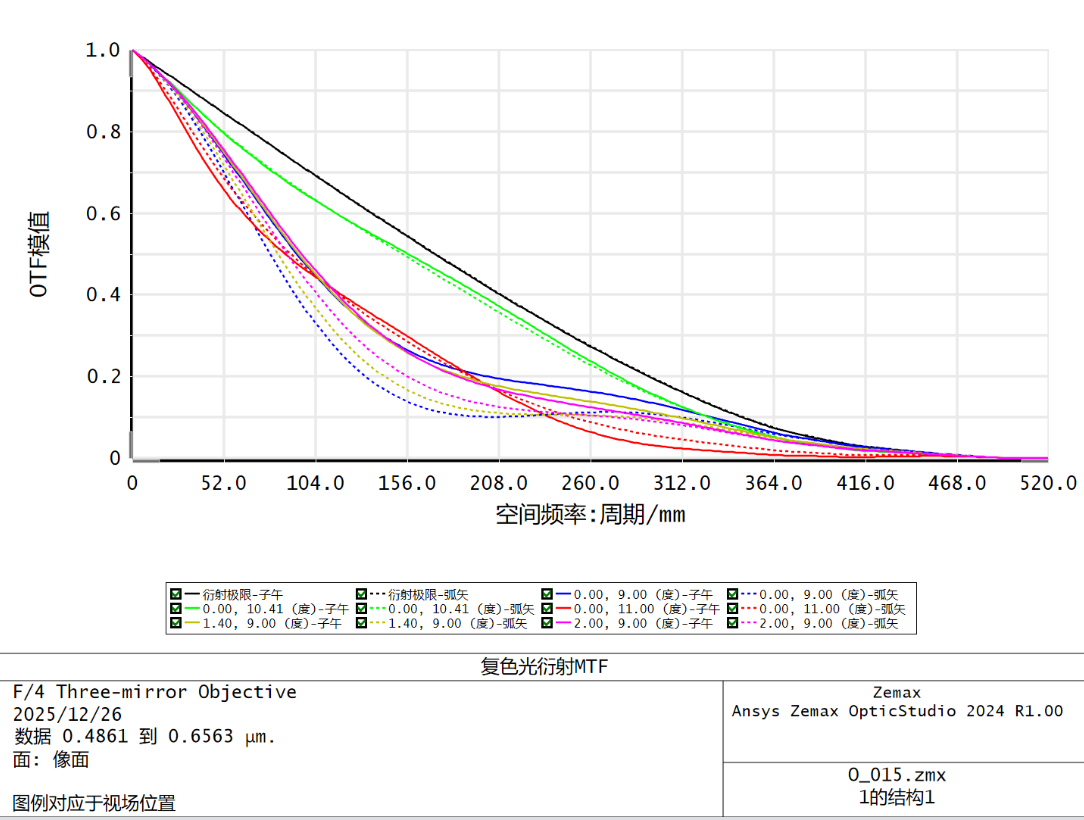
效果得到了改善，但系统发生较大变换，不符合设计要求。

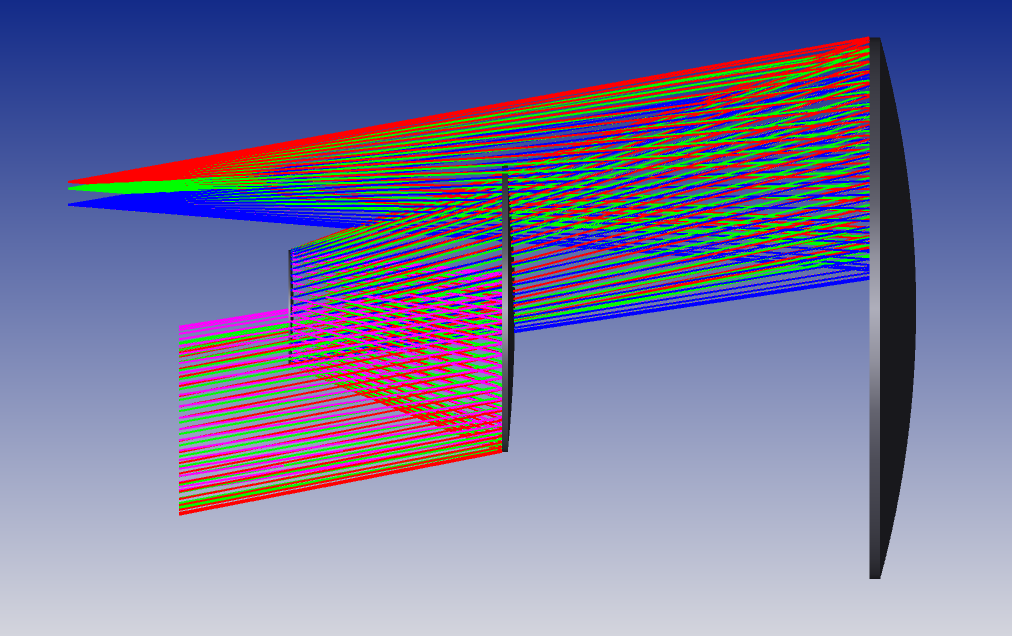
返回上一步的优化结果

添加镜间距控制操作数，主镜和次镜之间的距离，次镜和三镜之间的间距控制在150mm以内,上一布优化结果主镜和次镜之间的距离是500mm左右，主镜和三镜之间的距离900mm左右。

改为偶次非球面并将二次项和四次设置为变量进行优化

优化结果

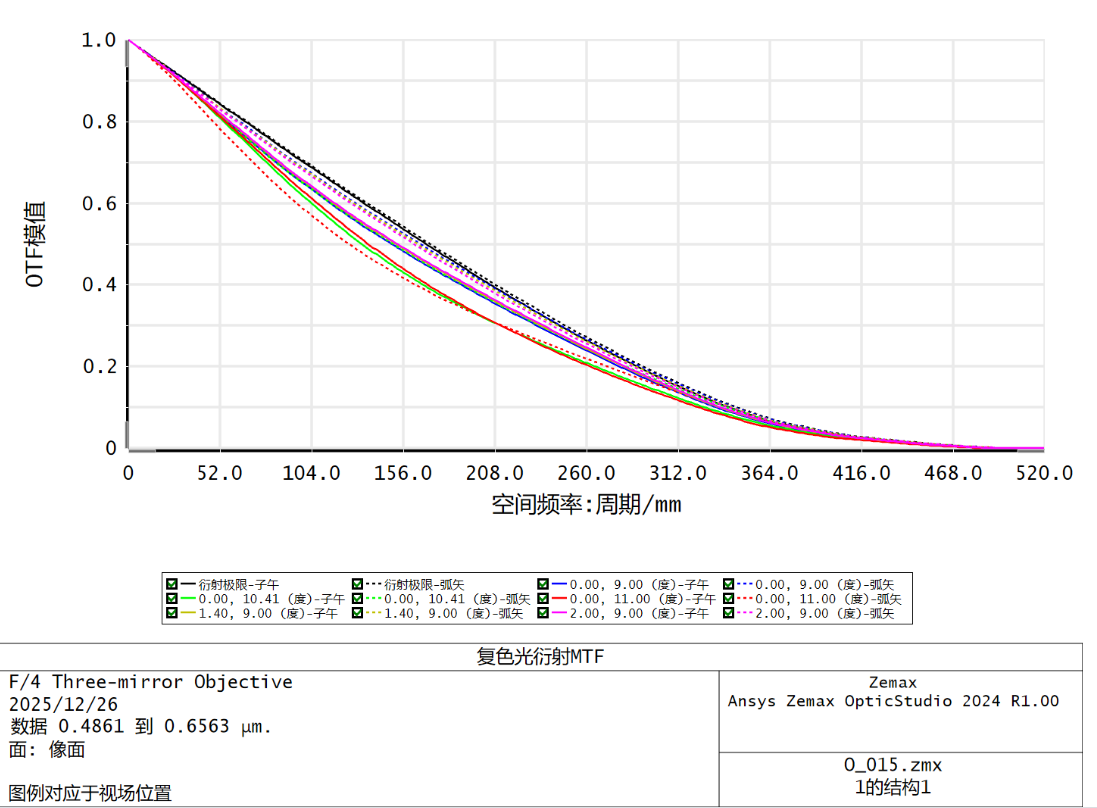
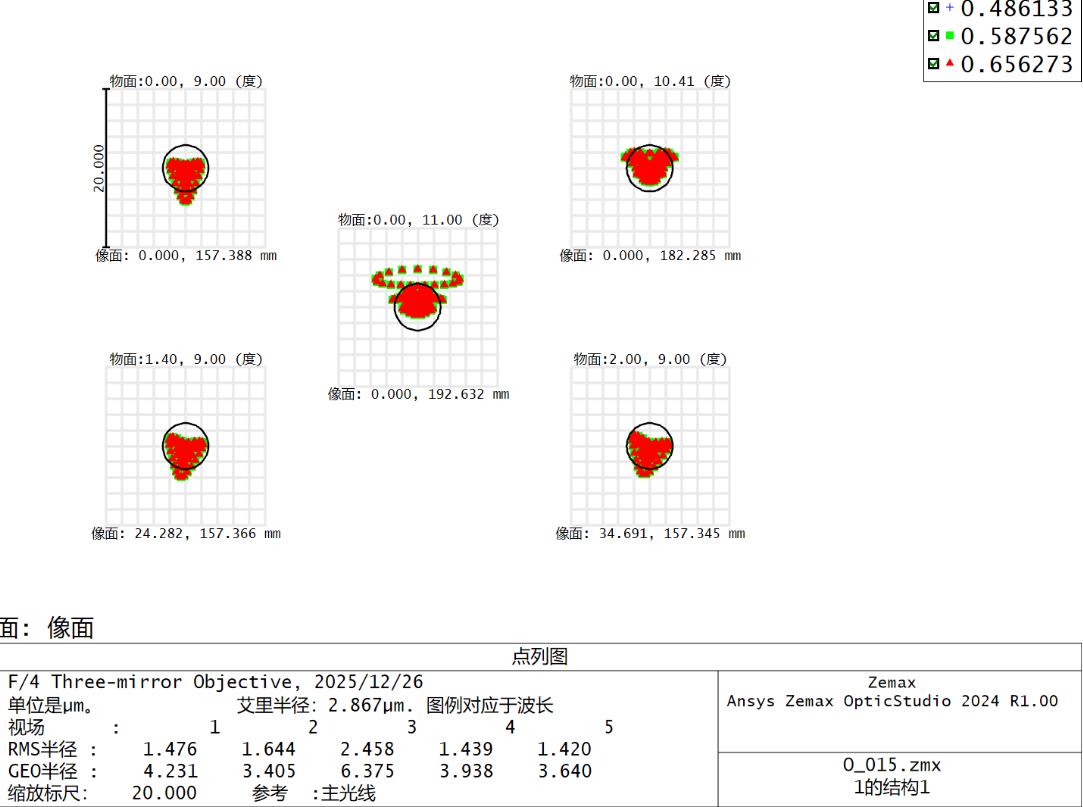
引入六次项变量

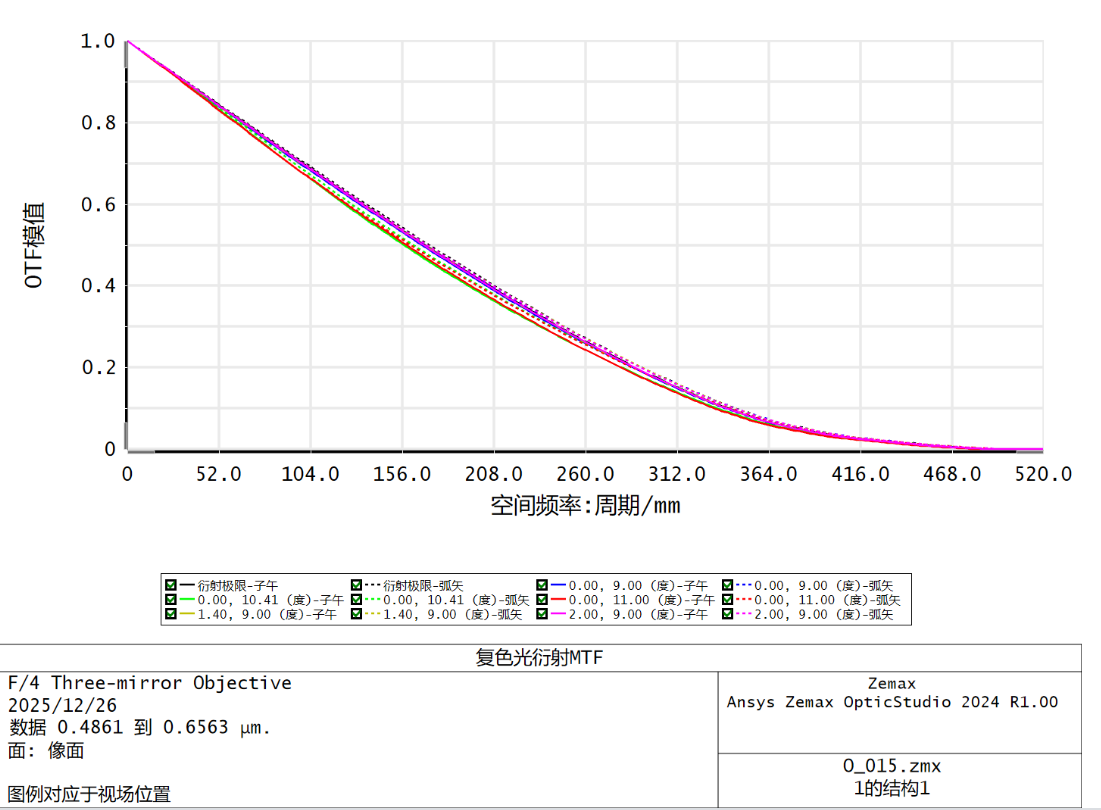
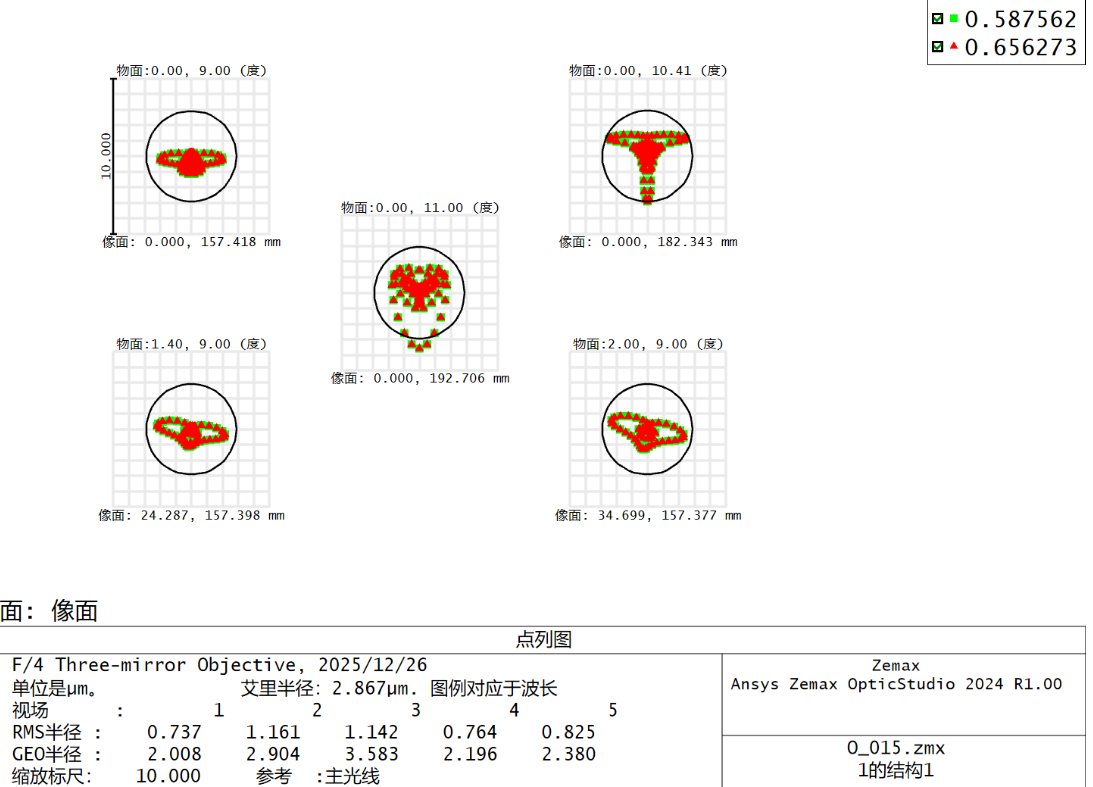
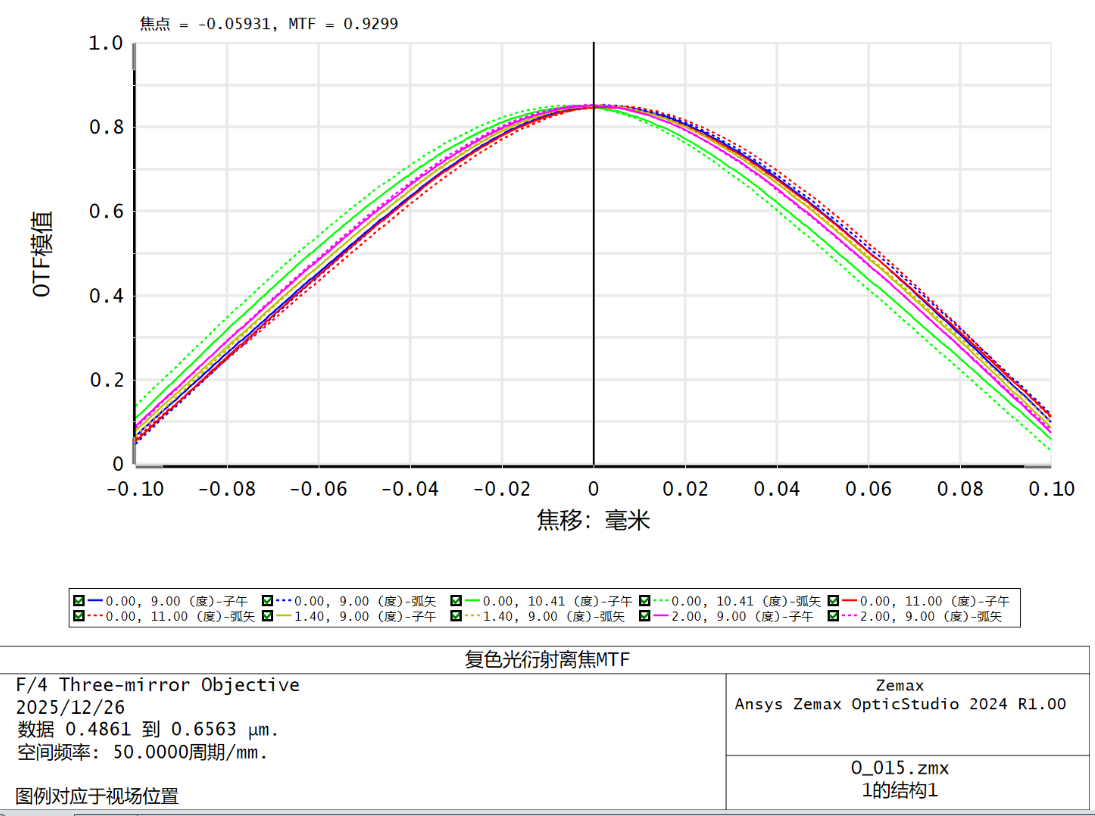
优化效果较好，传递函数和点列半径非常接近衍射极限，离焦曲线最高点统一。