剑指 Offer 33. 二叉搜索树的后序遍历序列

最新推荐文章于 2022-03-08 14:08:32 发布

原创最新推荐文章于 2022-03-08 14:08:32 发布 · 151 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #数据结构 #leetcode #二叉树 #dfs

python 专栏收录该内容

60 篇文章

订阅专栏

本文介绍如何通过递归方法判断一个整数数组是否符合二叉搜索树的后序遍历特性，提供了一段Python代码实现。关键在于理解后序遍历的规律并运用在算法设计中。

题目描述：
输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回 true，否则返回 false。

题解：
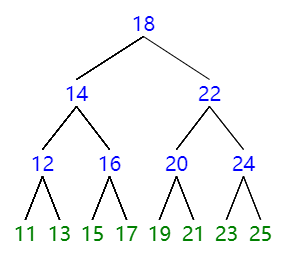
有如下一棵二叉搜索树：左节点值<根节点值<右节点值

输入：[11,13,12,15,17,16,14,19,21,20,23,25,24,22,18]
输出：True
二叉搜索树后序遍历特点：
1.构成：左子树（所有值比根节点小）+右子树（所有值比根节点大）+根节点
递归方法:
1.结束条件: i >= j，说明只有一个节点或者没有节点，无需进行迭代，直接返回True.
2.确定搜索区间 [i,j]，并设置一个移动游标p，list[j]是根节点。
3.移动游标p，寻找第一个大于list[j]的节点位置，设为m
4.将整个list分成 [i,m-1] (右子树)+[m,j-1] (左子树)+[j] (根节点)
5.右子树已经判断为正确的后序遍历结果，只需要判断左子树区间的值是否都大于根节点（判断左子树部分是否为后序遍历结果）
6.返回值:
p == j 判断子树正确
recur(i, m - 1) 判断左子树区间是否正确
recur(i, m - 1) 判断右子树区间是否正确

class Solution:
    def verifyPostorder(self, postorder: List[int]) -> bool:
        def recur(i,j):
            if i >= j: #说明只有一个节点或者没有节点
                return True
            p = i
            while postorder[p] < postorder[j]:
                p += 1
            m = p
            while postorder[p] > postorder[j]:
                p += 1
            return p == j and recur(i,m - 1) and recur(m, j - 1)
        return recur(0,len(postorder) - 1)