33. 二叉搜索树的后序遍历序列

剑指 Offer 33. 二叉搜索树的后序遍历序列

LCR 152. 验证二叉搜索树的后序遍历序列

输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回 true，否则返回 false。假设输入的数组的任意两个数字都互不相同。

参考以下这颗二叉搜索树：

     5
    / \
   2   6
  / \
 1   3

示例 1：

输入: [1,6,3,2,5]
输出: false

示例 2：

输入: [1,3,2,6,5]
输出: true

提示：

• 数组长度 <= 1000

解题思路

在后序遍历得到的序列中，最后一个数字是树的根节点的值。又由于是二叉搜索树，且没有重复数字，故数组中前面的数字可以分为两部分：第一部分是左子树节点的值，它们都比根节点的值小；第二部分是右子树节点的值，它们都比根节点的值大。

由此我们可以这样做：

1. 找到根节点
2. 从头遍历当前区间中的值，找到第一个不小于根节点的值，此时，该值左边的数都小于根节点是根节点的左子树，剩下的就应该是右子树，右子树中的值都需要大于根节点的，否则就不能构成二叉搜索树。

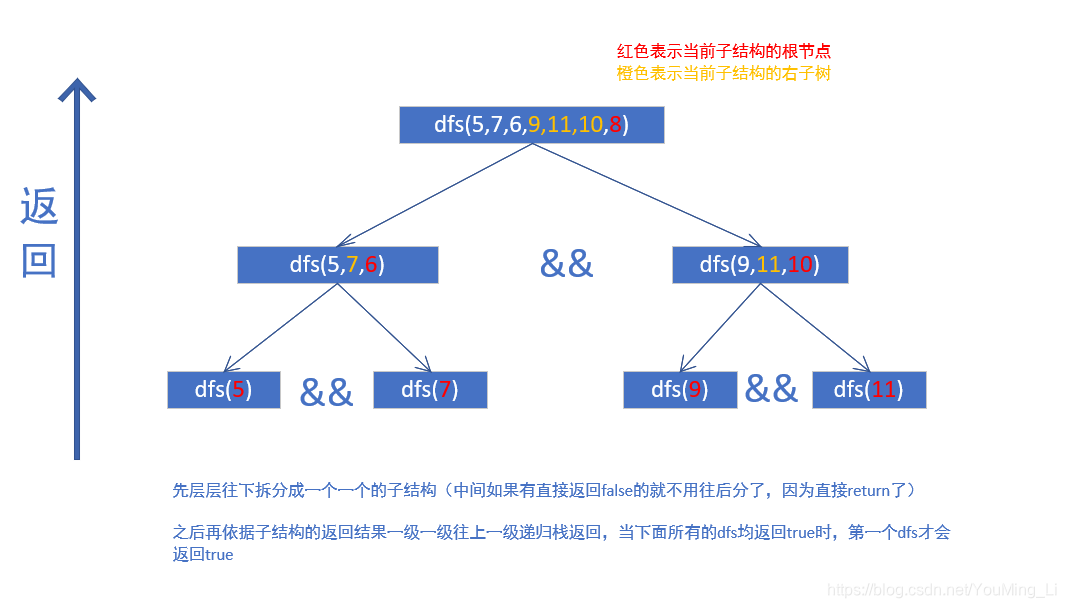
如数组{5,7,6,9,11,10,8}，后续遍历最后一个数字8就是根节点的值。前面5,7,6均小于8，是左子树，此时我们判断剩下的9,11,10是否都大于8,如果都大于8，说明他们可以作为根节点的右子树。之后可以用同样的方法确定与数组每一部分对应的子树的结构。这其实就是一个递归的过程。

对于递归回溯，大家肯定都知道是什么，看别人的代码也基本可以看懂，但是自己去写的时候，总感觉不是那么回事。这就是对递归回溯的整个过程没有思考清楚，本人建议可以自己多画几次递归回溯的流程图，去思考清楚是怎么回溯的，这样自己写的时候才能迅速的反应过来。记住一点，每一次递归都是调用了方法自身，都会开辟一个新的方法栈，只有遇到return语句或者当前方法栈运行结束才会往回回溯。否则上一级栈会一直等着他的下一级栈回来。

Java代码

class Solution {
    public boolean verifyPostorder(int[] postorder) {
        if(postorder == null || postorder.length == 0) return true;
        return dfs(postorder,0,postorder.length - 1);
    }
    
    public boolean dfs(int[] postorder,int start,int end){
        if(start >= end) return true;//分到只剩下一个数了，只有一个树节点肯定可以构成二叉搜索树
        int root = postorder[end];//当前子结构的根节点
        int i = start;//i用于找到第一个大于子结构根节点的值
        while(i < end && postorder[i] < root) i++;
        //从i到end-1就应该是右子树了，所有的值都应该大于root
        //如果有不大于root的，说明无法构成二叉搜索树
        for(int j = i;j < end;j++){
            if(postorder[j] < root){
                return false;
            }
        }
        //递归判断左右子树是否也符合二叉搜索树的性质
        return dfs(postorder,start,i - 1) && dfs(postorder,i,end - 1);
    }
}

Go代码

func verifyTreeOrder(postorder []int) bool {
    // 后续最后一个元素是根节点，然后由于是二叉搜索树，所以小于根节点的是左子树，反之，是右子树
    if len(postorder) == 0 {
        return true
    }
    return dfs(postorder,0,len(postorder) - 1)
}

// 全局坚持左闭右闭
func dfs(postorder []int,left,right int) bool {
    if left >= right { // 只有一个节点，或者没有节点的时候，是一棵二叉搜索树
        return true
    }
    root := postorder[right]
    l := left
    for l < right {
        if postorder[l] < root {
            l++
        } else {
            // 遇到一个不小于的时候就退出for，此时l就是第一个不小于root的元素，也就是右子树第一个元素
            break
        }
    }
    
    // 现在l到right之间的就是右子树，需要所有数字都大于root
    for i := l ;i < right;i++ {
        if postorder[i] < root {
            return false
        }
    }
    return dfs(postorder,left,l - 1) && dfs(postorder,l,right - 1)
}

---

扩展题：LeetCode 1008. 前序遍历构造二叉搜索树

1008. 前序遍历构造二叉搜索树

返回与给定前序遍历 preorder 相匹配的二叉搜索树（binary search tree）的根结点。

(回想一下，二叉搜索树是二叉树的一种，其每个节点都满足以下规则，对于 node.left 的任何后代，值总 < node.val，而 node.right 的任何后代，值总 > node.val。此外，前序遍历首先显示节点 node 的值，然后遍历 node.left，接着遍历 node.right。）

题目保证，对于给定的测试用例，总能找到满足要求的二叉搜索树。

示例：

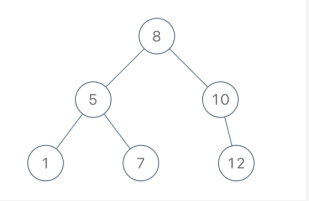
输入： [8,5,1,7,10,12]
输出： [8,5,10,1,7,null,12]

提示：

• 1 <= preorder.length <= 100
• 1 <= preorder[i] <= 10^8
• preorder 中的值互不相同

解题思路

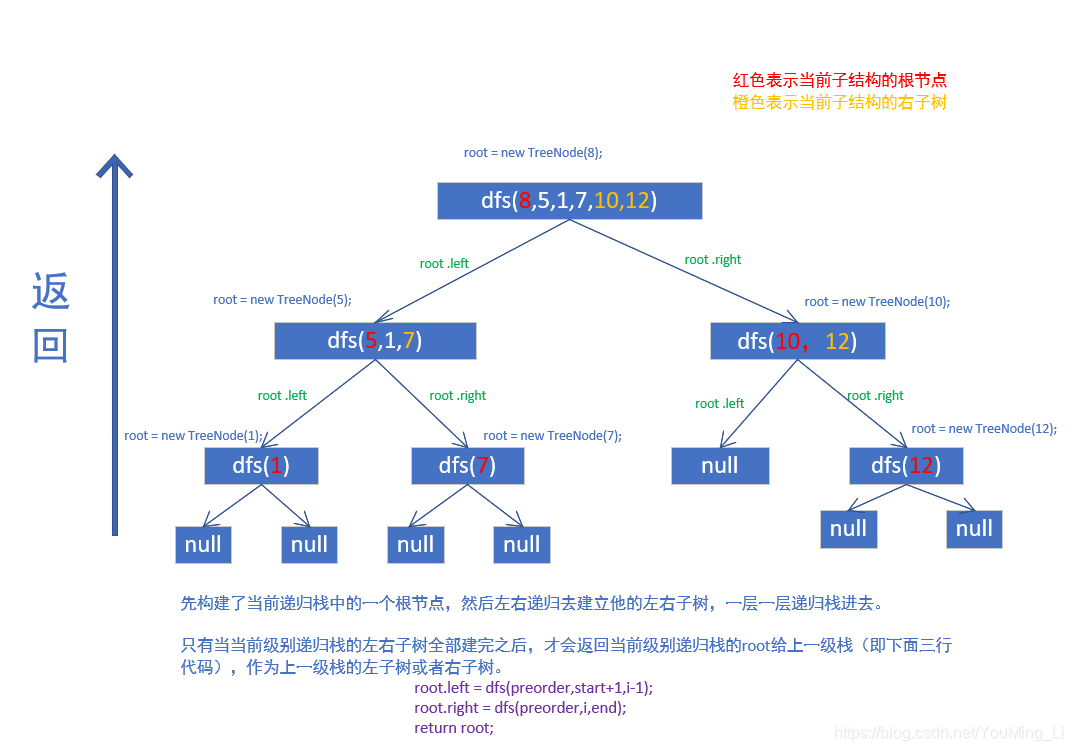
这就是剑指offer p182的相关题目，是上一题的扩展题，上题是判断能否构成二叉搜索树，而这题是告知一定可以构成二叉搜索树，让我们构造出该树。其实就是换汤不换药。思路与上题一致，这里换成了前序遍历罢了。为了加深对递归回溯的理解，仍然画了一个图，以[8,5,1,7,10,12]为例。

Java代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode bstFromPreorder(int[] preorder) {
        if(preorder == null || preorder.length == 0) return null;
        TreeNode root = dfs(preorder,0,preorder.length - 1);
        return root;
    }
    
    private TreeNode dfs(int[] preorder,int start,int end){
    	//注意这里条件与上稍有不同,'='时，需要返回new TreeNode(preorder[start]),为了统一，去掉‘=’
        if(start > end) return null;
        TreeNode root = new TreeNode(preorder[start]);
        //找到第一个不小于根节点值的值，从而划分左右子树，继续递归下去
        int i = start+1;//保存第一个大于根节点值的索引
        while(i <= end && preorder[i] < root.val ) i++;
        root.left = dfs(preorder,start+1,i-1);
        root.right = dfs(preorder,i,end);
        return root;
    }
}

Go代码

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func bstFromPreorder(preorder []int) *TreeNode {
    if len(preorder) == 0 {
        return nil
    }

    // 只要递归过程中，全程坚持左闭右闭或者左闭右开，区间就不容易乱
    // 这里选择左闭右闭
    root := dfs(preorder,0,len(preorder) - 1)
    return root
}

func dfs(preorder []int,left,right int) *TreeNode {
    if left > right {
        return nil
    }
    if left == right {
        return &TreeNode{Val:preorder[left]}
    }
    root := &TreeNode{Val :preorder[left]}
    // 找到左子树区间
    l := left + 1
    for l <= right {
        if preorder[l] < root.Val {
            l++
        } else {
            break
        }
    }
    // l此时是不小于root.Val的第一个数，也就是右子树的第一个数
    root.Left = dfs(preorder,left + 1,l - 1)
    root.Right = dfs(preorder,l,right)
    return root 

}

举一反三

如果面试题要求处理一棵二叉树的遍历序列，则可以先找到二叉树的根节点，再基于根节点把整个树的遍历序列拆分为左右子序列，然后递归的处理这两个序列。上面两题都是这个思路，剑指offer 7. 重建二叉树应用的也是该思路。