jzoj 5836.【省选&A组模拟2018.8.21】Sequence dp+矩阵乘法

Description

Input

Output

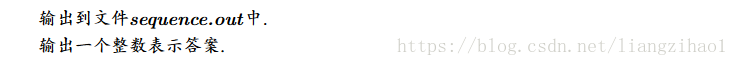
Sample Input

Input 1
2 1 3
1 3
Input 2
5 6 3
3 1 2 1 2
Input 3
9 980007 7
4 7 2 1 3 3 6 6 7

Sample Output

Output 1
7
Output 2
987
Output 3
608313080

Data Constraint

Hint

分析：
我们先不考虑加数情况，设$f[i]$为以第$i$个位置结尾的子序列有多少个（不包括前面出现的）。
设$last[x]$为$x$上次出现的位置，有

$$f[i]=\sum_{j=last[x]}^{i-1}f[j]$$
因为$last$的去前面的子序列加入$last$这个位置就与现在这个重复了，不能算。而$f[last]$到$f[i-1]$的也是排除了前面相同的，所以正确性显然。
而$\sum_{i=1}^{n}f[i]$就是答案，初始时$last[x]=0$，$f[0]=1$，因为可以从空序列转移。
考虑加一个数字，显然我们加一个$last[x]$最小的数一定最优，然后更新$last[x]$。这个可以自己找两个不同$last$比较一下。如果都没出现过，就随便放。记录一个前缀和，这样复杂度就是$O(n+mk)$，轻松拿到$78$分。
然后我们发现，这个东西是有循环的。具体说，当我们放了$k$个数后就开始循环了。因为已经放过的一定$last[x]>n$，这样我们一定先会放完$k$个；然后$last$大小就与这$k$个位置有关了，可以知道，先放的在一下个循环也会先放，于是构成循环，也就是$last=i-k$。因为我们最终的答案是一个前缀和，考虑用这个递推。
因为$sum[i]=sum[i-1]-sum[i-k-1]+sum[i-1]$，可以写成一个$k+1$维向量。然后就可以矩阵快速幂了。
时间复杂度为$O(k^3logm)$。

代码：

#include <iostream>
#include <cmath>
#include <cstdio>
#define LL long long

const int maxn=2e6+7;
const LL mod=1e9+7;

using namespace std;

LL f[maxn],sum[maxn],a[maxn];
int l[107];
LL n,m,k,d;

struct rec{
    LL a[107][107];
}b,c;

void mul(rec a,rec b,rec &c)
{   
    for (int i=1;i<=d;i++)
    {
        for (int j=1;j<=d;j++) c.a[i][j]=0;
    }
    for (int l=1;l<=d;l++)
    {
        for (int i=1;i<=d;i++)
        {
            for (int j=1;j<=d;j++)
            {
                c.a[i][j]=(c.a[i][j]+a.a[i][l]*b.a[l][j]%mod)%mod;
            }
        }
    }
}

void solve(LL deg)
{
    for (int i=1;i<=d;i++) b.a[i][i]=1;
    while (deg)
    {
        if (deg&1) mul(b,c,b);
        mul(c,c,c); deg/=2;
    }
}

int main()
{
    freopen("sequence.in","r",stdin);
    freopen("sequence.out","w",stdout);
    scanf("%lld%lld%lld",&n,&m,&k);
    for (int i=1;i<=n;i++) scanf("%lld",&a[i]);
    sum[0]=1;   
    for (int i=1;i<=n;i++)
    {
        if (!l[a[i]]) f[i]=(f[i]+sum[i-1])%mod;
                 else f[i]=(f[i]+sum[i-1]+mod-sum[l[a[i]]-1])%mod;
        l[a[i]]=i;
        sum[i]=(sum[i-1]+f[i])%mod;
    }
    for (int i=n+1;i<=n+k;i++)
    {
        int x=0,t=0x3f3f3f3f;
        for (int j=1;j<=k;j++)
        {
            if (l[j]<t) t=l[j],x=j;
        }
        if (!l[x]) f[i]=(f[i]+sum[i-1])%mod;
              else f[i]=(f[i]+sum[i-1]+mod-sum[l[x]-1])%mod;
        l[x]=i;
        sum[i]=(sum[i-1]+f[i])%mod;
    }
    if (m<=k)
    {
        printf("%d",(sum[n+m]+mod-1)%mod);
    }
    else
    {       
        d=k+1;      
        for (int i=1;i<=d-1;i++) c.a[i+1][i]=1;
        c.a[1][d]=mod-1; c.a[d][d]=2;               
        solve(m-k);     
        LL ans=0;
        for (int i=1;i<=d;i++) ans=(ans+sum[n+i-1]*b.a[i][d]%mod)%mod;
        ans=(ans+mod-1)%mod;
        printf("%lld",ans);
    }
}