leetcode 1218. Longest Arithmetic Subsequence of Given Difference（给定差值的最长算术子序列）

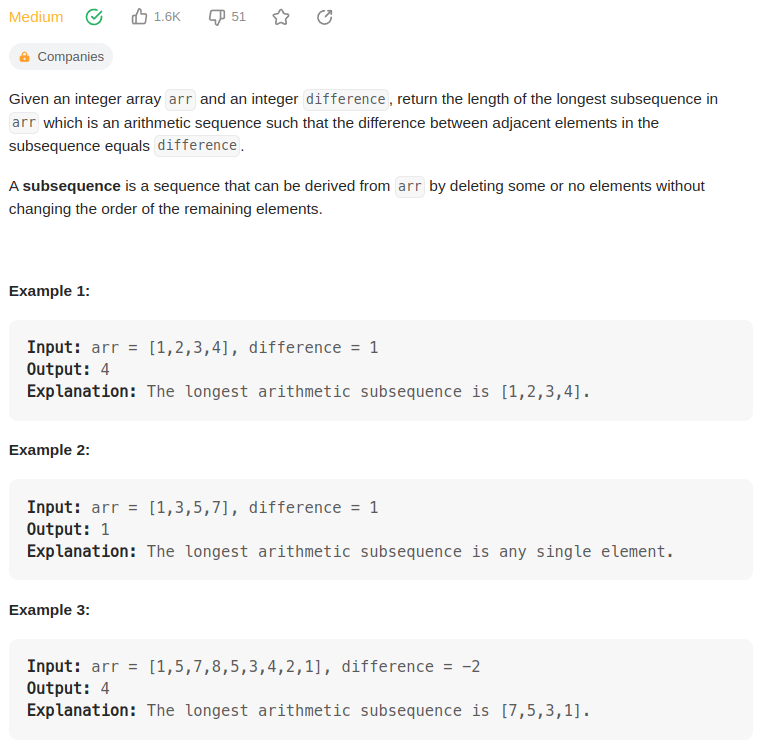
给数组arr和一个差值difference, 不打乱arr中数字的顺序，抽取最长的子序列，使序列中每相邻两个元素的差值为difference.
求满足条件的最长子序列的长度。

思路：

DP

因为差值difference是固定的，每抽取一个元素，它前面的元素也是固定的。
比如现在的元素为arr[ i ], 那么它前面的元素一定是arr[ i ] - difference.
所以到arr[ i ]为止的序列长度也是固定的。

只需要统计到arr[ i ]为止的子序列长度。
记下这些长度的最大值。

dp数组可以用一个hashMap, 保存(arr[ i ], 到arr[ i ]为止的子序列长度),
也可以用数组。

（1）HashMap

    public int longestSubsequence(int[] arr, int difference) {
        Map<Integer,Integer> dp = new HashMap<>();
        int n = arr.length;
        int res = 0;

        for(int i = 0; i < n; i++) {
            dp.put(arr[i], dp.getOrDefault(arr[i]-difference, 0)+1);
            res = Math.max(res, dp.get(arr[i]));
        }

        return res;
    }

(2) 数组
直接下标取元素，速度更快，
为了节省存储空间，dp数组长度为arr的最大值-最小值+1.
但是要注意dp中的下标是arr[ i ] - min. 并不是arr的下标 i。

    public int longestSubsequence(int[] arr, int difference) {
        int min = Integer.MAX_VALUE;
        int max = Integer.MIN_VALUE;
        int res = 1;

        for(int num : arr) {
            min = Math.min(min, num);
            max = Math.max(max, num);
        }

        int[] dp = new int[max-min+1];
        for(int i = 0; i < arr.length; i++) {
            int cur = arr[i] - min;
            int pre = cur - difference;
            if(pre >= 0 && pre < dp.length) {
                dp[cur] = dp[pre] + 1;
                if(dp[cur] > res) res = dp[cur];
            } else {
                dp[cur] = 1;
            }
        }
        return res;
    }