leetcode 875. Koko Eating Bananas（koko吃香蕉）-优快云博客

本文链接：https://blog.youkuaiyun.com/level_code/article/details/129438686

文章介绍了如何利用二分查找算法解决一个关于吃香蕉的问题。在给定每堆香蕉的数量和可吃香蕉的总小时数下，找到每小时至少需要吃多少个香蕉才能在限制时间内吃完所有香蕉。关键在于优化二分查找过程，避免浮点数运算，提高效率。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

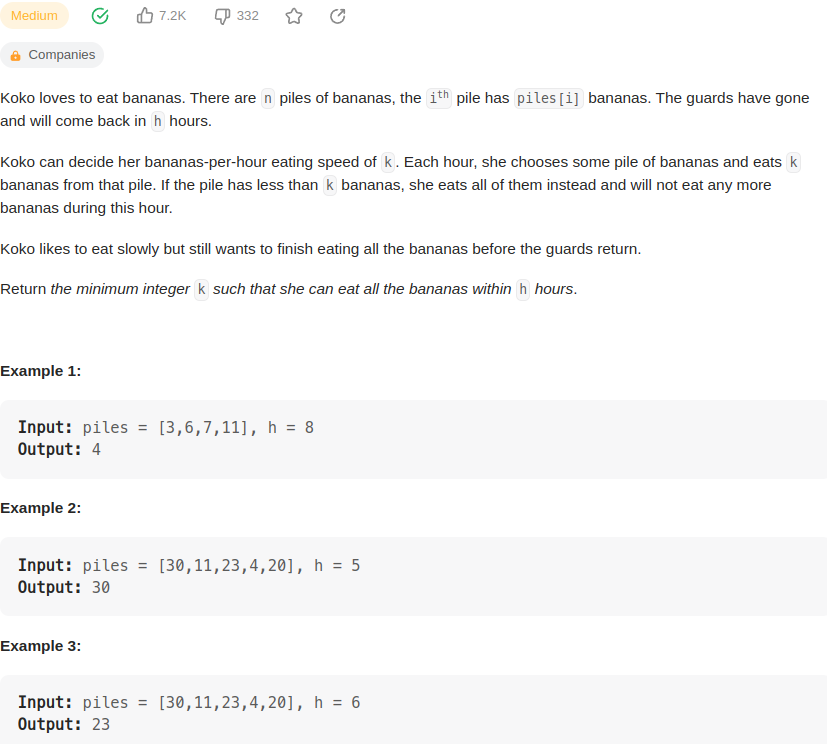
在这里插入图片描述

piles数组里面是每堆香蕉里面有多少个香蕉，
现在有h小时可以吃香蕉，每小时只能吃一个堆，
定义每小时能吃k个香蕉，k >= piles[i], 那么第 i 堆一次吃完，否则下一小时继续吃。
问k为多少时可以在h小时内把香蕉吃完。

思路：

和2187题很像。

假设数组长度为n,
如果每小时吃max(piles)个香蕉，需要n小时。题目中n<=h.

所以知道k的右边界是max(piles),
左边界是1，最少每小时吃1个。

然后在1和max(piles)之间找到k,
让 sum (ceil (piles[i] / k)) = h

所以用到 binary search.

这里的binary search需要注意的是，当sum(ceil(piles[i]/mid)) == h时，
right仍然能减小，可以找到更小的满足条件的k，
但是，right == mid 而不是 right == mid-1,
因为不确定是否有更小的k满足条件，要把mid保留住。

    public int minEatingSpeed(int[] piles, int h) {
        int n = piles.length;
        int maxNum = 0;
        for(int pile : piles) {
            maxNum = Math.max(maxNum, pile);
        }

        int left = 1;
        int right = maxNum;

        while(left < right) {
            int mid = left + (right-left) / 2;
            double curH = 0;
            for(int pile : piles) curH += Math.ceil((double)pile/mid);
            
            if((int)curH <= h) right = mid;
            else left = mid+1; 
        }
        return left;
    }
}

上面的方法比较慢，慢在哪里呢，可以看到ceil这个函数要传double进去，返回的也是double,
因此需要在int 和 double之间来回转换。

下面不用ceil函数，
可以想一下，ceil(1/mid) = 1, ceil(mid-1/mid) = 1,
只需要让这两个边界满足即可，因此给piles[i] + mid - 1,

    public int minEatingSpeed(int[] piles, int h) {
        int n = piles.length;
        int maxNum = 0;
        for(int pile : piles) {
            maxNum = Math.max(maxNum, pile);
        }

        int left = 1;
        int right = maxNum;

        while(left < right) {
            int mid = left + (right-left) / 2;
            int curH = 0;
            for(int pile : piles) curH += (pile+mid-1)/mid;
            if(curH <= h) right = mid;
            else left = mid+1; 
        }
        return left;
    }