Matlab/Simulink 电池仿真模型搭建之旅-优快云博客

Matlab/simulink仿真模型搭建（电池相关）本店可接锂电池或电池包建模搭建单体电池方面： 1、电池等效电路模型搭建（RC模型） 2、电池特征参数辨识(离线、在线、自适应） 3、电池SOC估计（基于扩展卡尔曼滤波方法）电池均衡管理方面： 1、可搭建锂电池电池包的主动均衡仿真模型（基于变压器型号） 2、可设计基于本控制策略（平均差值、极差等）、模糊逻辑均衡控制器、多目标优化均衡控制器的模型搭

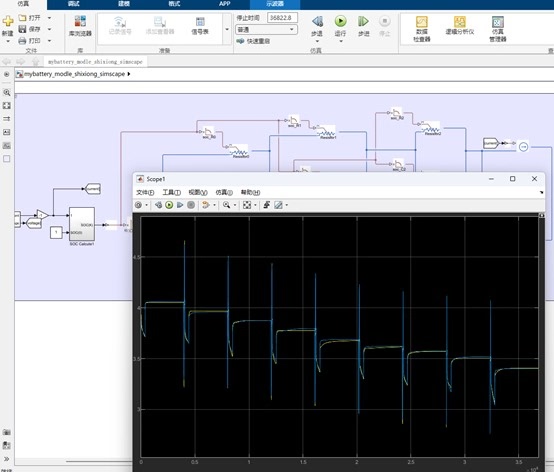
在电池研究与应用领域，Matlab/Simulink 就像是一个神奇的魔法箱，能帮我们搭建出各种逼真的电池仿真模型。今天咱就来唠唠关于电池相关模型搭建那些事儿。

单体电池模型搭建

电池等效电路模型搭建（RC 模型）

电池等效电路模型中的 RC 模型是个经典。想象一下，电池就像是由一些电阻（R）和电容（C）组成的电路结构，来模拟电池内部复杂的电化学特性。在 Matlab/Simulink 里搭建这个模型，我们可以这样开始：

% 创建一个新的 Simulink 模型
new_system('battery_RC_model');
open_system('battery_RC_model');

% 添加电源模块
power_source = add_block('simulink/Sources/DC Voltage Source',...
    'battery_RC_model/power_source');
set_param(power_source, 'Voltage', '12'); % 设置电源电压为 12V

% 添加电阻模块
R1 = add_block('simulink/Electrical Sources and Elements/Resistor',...
    'battery_RC_model/R1');
set_param(R1, 'Resistance', '0.1'); % 设置电阻值为 0.1 欧姆

% 添加电容模块
C1 = add_block('simulink/Electrical Sources and Elements/Capacitor',...
    'battery_RC_model/C1');
set_param(C1, 'Capacitance', '0.01'); % 设置电容值为 0.01 法拉

这里，我们通过 addblock 函数在模型中添加了电源、电阻和电容模块，并且通过 setparam 函数设置了它们的参数。这个简单的代码片段，就是搭建 RC 模型的基础，后续还可以根据实际需求添加更多的电路元件和连接。

电池特征参数辨识(离线、在线、自适应）

参数辨识是让模型更贴合实际电池特性的关键步骤。以离线参数辨识为例，我们通常先采集大量电池在不同工况下的数据，然后利用优化算法去寻找最能匹配这些数据的模型参数。

% 假设已经采集到的数据
voltage_data = [11.8, 11.6, 11.4]; % 电压数据
current_data = [1, 2, 3]; % 电流数据

% 定义目标函数，用于评估模型与实际数据的误差
objective_function = @(params) sum((battery_model(params, current_data) - voltage_data).^2);

% 初始参数猜测
initial_params = [0.1, 0.01]; % 初始电阻和电容值

% 使用优化算法寻找最优参数
optimal_params = fminsearch(objective_function, initial_params);

这里，我们定义了一个目标函数 objective_function，它计算模型输出与实际数据之间的误差平方和。然后使用 fminsearch 这个优化算法，从初始参数猜测开始，寻找能使目标函数最小的最优参数。

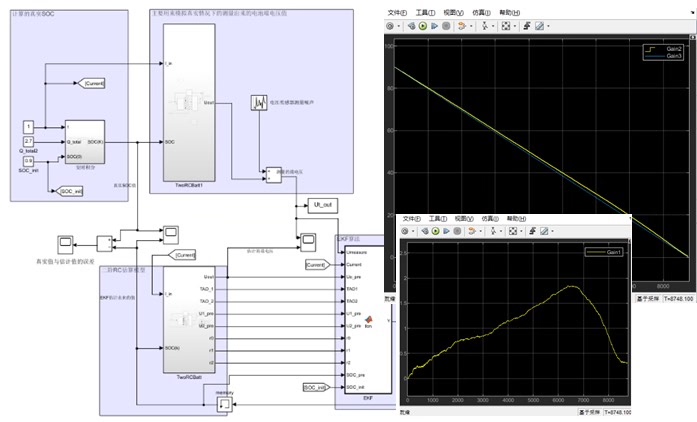
电池 SOC 估计（基于扩展卡尔曼滤波方法）

电池荷电状态（SOC）估计对于了解电池剩余电量至关重要。扩展卡尔曼滤波（EKF）是常用的方法之一。

% 定义状态转移函数
f = @(x, u) [x(1) - u / capacity; x(2)];
% 这里 x(1) 是 SOC，x(2) 是其他状态变量（假设），u 是电流，capacity 是电池容量

% 定义观测函数
h = @(x) x(1);

% 初始化状态和协方差
x_hat = [0.5; 0]; % 初始 SOC 估计为 0.5，其他状态初始值为 0
P = [0.01, 0; 0, 0.01]; % 初始协方差矩阵

% 过程噪声协方差
Q = [0.001, 0; 0, 0.001];
% 观测噪声协方差
R = 0.01;

for k = 1:length(current_data)
    % 预测步骤
    x_hat_minus = f(x_hat, current_data(k));
    F = [1, 0; 0, 1]; % 状态转移矩阵的雅可比矩阵（这里简化假设为单位矩阵）
    P_minus = F * P * F' + Q;

    % 更新步骤
    y = voltage_data(k);
    H = [1, 0]; % 观测矩阵的雅可比矩阵
    K = P_minus * H' / (H * P_minus * H' + R);
    x_hat = x_hat_minus + K * (y - h(x_hat_minus));
    P = (eye(2) - K * H) * P_minus;
end

这段代码展示了 EKF 算法在 SOC 估计中的基本步骤。通过状态转移函数 f 和观测函数 h，不断地预测和更新 SOC 的估计值 x_hat 以及协方差矩阵 P。

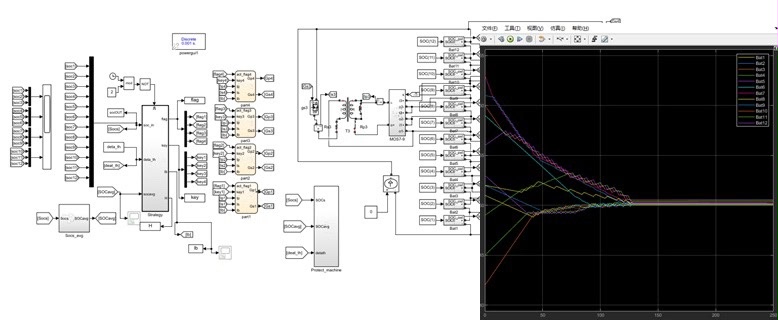
电池均衡管理方面

可搭建锂电池电池包的主动均衡仿真模型（基于变压器型号）

主动均衡能有效提升电池包整体性能。以基于变压器的主动均衡模型为例，在 Simulink 中搭建时，我们要考虑变压器的特性以及电池之间的能量转移。

% 创建主动均衡模型
new_system('active_balancing_model');
open_system('active_balancing_model');

% 添加电池模块（假设多个单体电池）
for i = 1:10
    battery_i = add_block('simulink/Electrical Sources and Elements/Battery',...
        ['active_balancing_model/battery_' num2str(i)]);
    set_param(battery_i, 'Initial voltage', '3.7'); % 假设单体电池初始电压 3.7V
end

% 添加变压器模块
transformer = add_block('simulink/Electrical Sources and Elements/Transformer',...
    'active_balancing_model/transformer');
% 设置变压器参数，比如变比等

这里，我们先创建了多个单体电池模块，并设置了初始电压。然后添加了变压器模块，后续还需要连接各个电池与变压器，并添加控制逻辑，来实现电池之间的能量均衡转移。

可设计基于本控制策略（平均差值、极差等）、模糊逻辑均衡控制器、多目标优化均衡控制器的模型搭建

以平均差值控制策略为例，思路就是计算各个电池电压与平均电压的差值，根据差值来决定能量转移方向。

% 假设已经获取到各个电池的电压
battery_voltages = [3.6, 3.8, 3.7];

% 计算平均电压
average_voltage = mean(battery_voltages);

% 计算电压差值
voltage_differences = battery_voltages - average_voltage;

% 根据差值决定能量转移，这里简单示例，实际需更复杂逻辑
for i = 1:length(battery_voltages)
    if voltage_differences(i) > 0
        % 该电池电压高，转移能量出去
        % 实际需实现能量转移代码
    elseif voltage_differences(i) < 0
        % 该电池电压低，接收能量
        % 实际需实现能量转移代码
    end
end

这段代码计算了电池电压与平均电压的差值，为基于平均差值的均衡控制提供了判断依据。而模糊逻辑均衡控制器和多目标优化均衡控制器则需要更复杂的逻辑设计，模糊逻辑要定义模糊规则和隶属度函数，多目标优化则要综合考虑多个性能指标进行优化。