【Carsim simulink联合仿真】根据文档复现递推最小二乘法估计轮胎侧偏刚度模型，文档详实

原创于 2025-12-16 16:00:00 发布 · 207 阅读

3 ·

CC 4.0 BY-SA版权

文章标签：

#hdfs

【Carsim simulink联合仿真】根据文档复现递推最小二乘法估计轮胎侧偏刚度模型，文档详实，代码规范

刚接手Carsim和Simulink联合仿真项目时，看着文档里那套递推最小二乘法估计轮胎侧偏刚度的模型，心里直打鼓——这玩意儿真能在线估计参数？实际操作后发现，只要处理好数据同步和算法迭代，还真能在仿真过程中看着参数蹭蹭收敛。

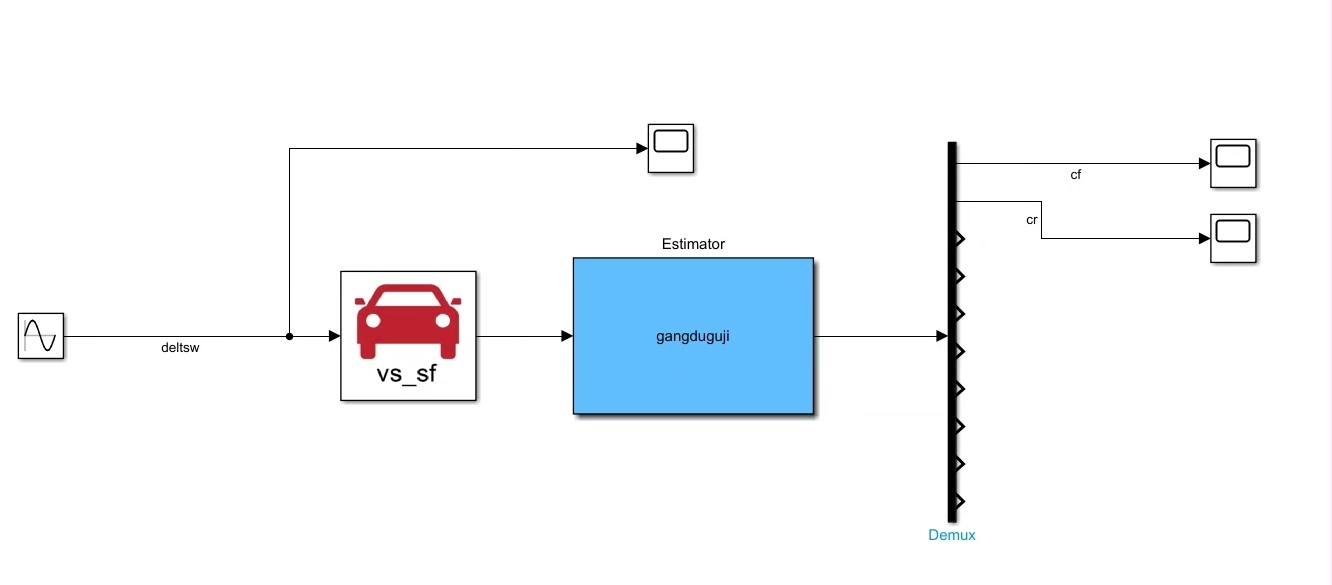
先说说模型搭建的坑。Carsim那头需要配置车辆动力学参数时，发现方向盘转角信号必须走Simulink输出通道，直接在Carsim里设置会丢失时间同步。解决办法是在Simulink里搞了个零阶保持器，硬核同步两边的采样时间：

function steering_angle = sync_signal(u)
    persistent last_value;
    if isempty(last_value)
        last_value = 0;
    end
    if ~isnan(u)
        last_value = u;
    end
    steering_angle = last_value;
end

这段代码里的持久变量像极了打游戏时的存档点，确保Carsim突然抽风丢信号时，方向盘转角不会跳变到姥姥家。

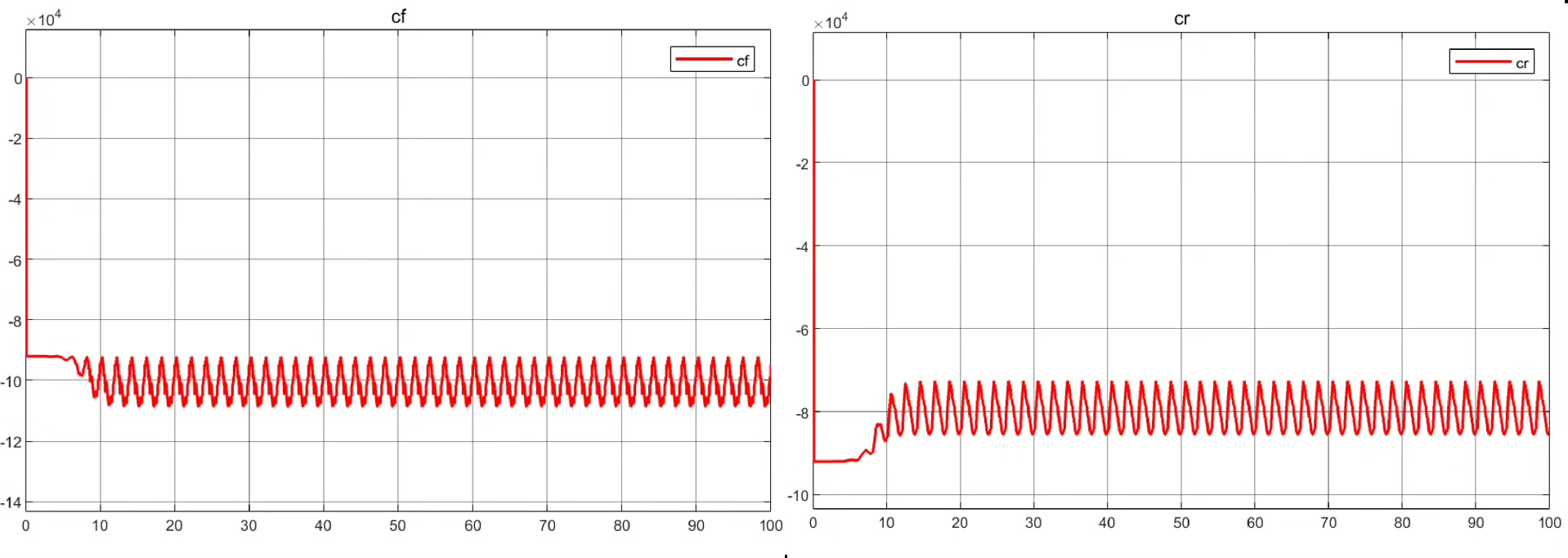
核心算法部分，递推最小二乘法的实现比教科书上的公式刺激多了。在Simulink里用Matlab Function模块实现时，发现直接用矩阵运算会触发诡异的维度错误。后来改用递推形式的标量计算才稳住局面：

function [theta, P] = RLS(y, phi, theta_prev, P_prev)
    K = P_prev * phi' / (1 + phi * P_prev * phi');
    theta = theta_prev + K * (y - phi * theta_prev);
    P = (eye(2) - K * phi) * P_prev;
    
    % 防止协方差矩阵膨胀
    P = 0.5*(P + P'); 
    P = P + 0.01*eye(2)*(trace(P)<1e-6);
end

这里两个骚操作很有意思：给协方差矩阵P加对称约束和小扰动，像极了给不安分的熊孩子系安全带。实测发现不加这两句的话，跑个二十秒仿真P矩阵就能膨胀到让Matlab怀疑人生。

跑仿真时看着参数估计曲线跳舞，前五秒像醉汉画龙，十秒后突然开窍似的往理论值靠拢。特别是侧向速度估计值跟Carsim理论输出的对比图，两条曲线从互相嫌弃到如胶似漆，强迫症都被治愈了。

最后说个血泪教训：Carsim的传感器噪声模块别手贱全开，特别是横摆角速度噪声超过0.5deg/s后，参数估计立马开启蹦迪模式。后来自己撸了个移动平均滤波器才镇住场子，果然数据预处理才是算法的亲妈。