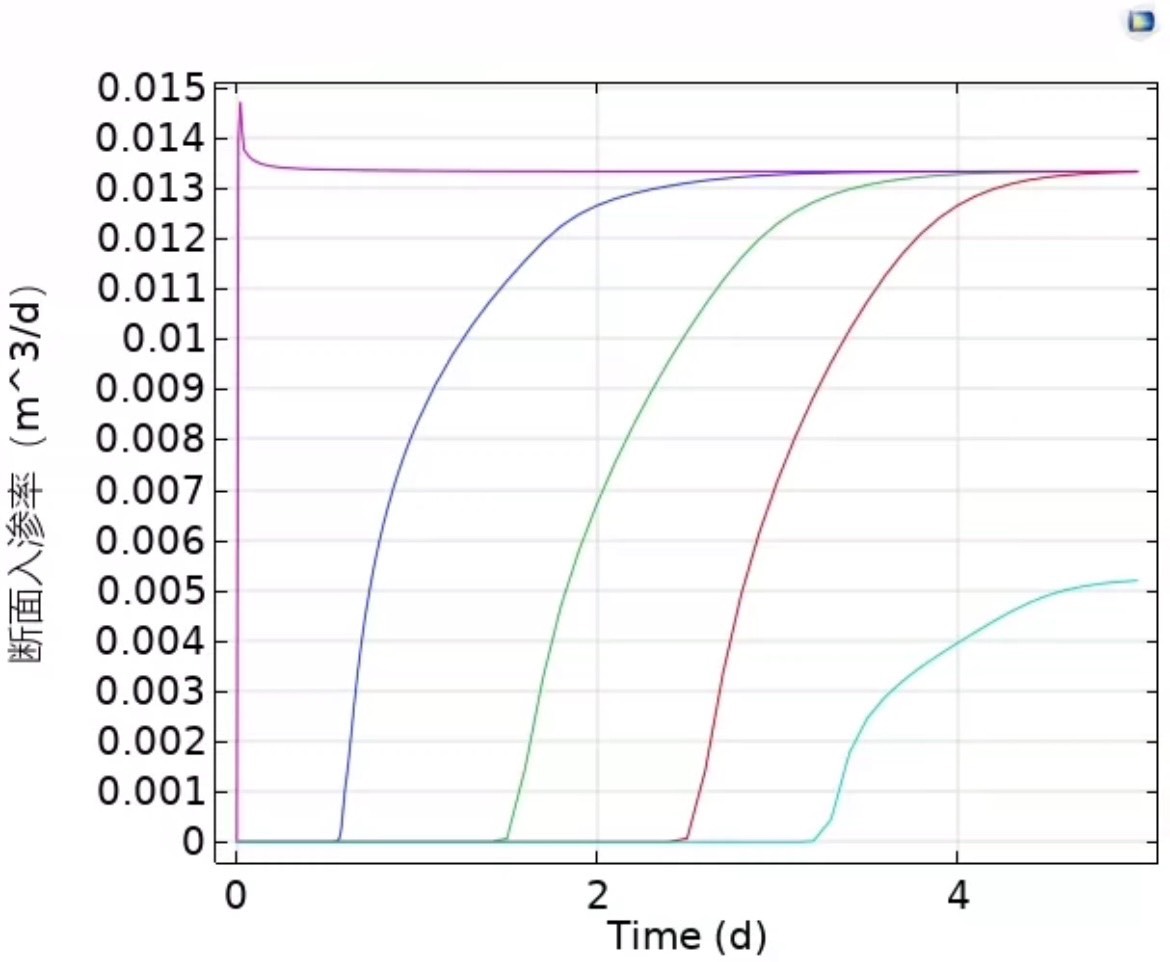
Comsol 非饱和裂隙土降雨入渗研究：复现之旅

comsol非饱和裂隙土降雨入渗研究，复现论文（侯晓萍,樊恒辉.基于COMSOL Multiphysics的非饱和裂隙土降雨入渗特性研究[J].岩土力学,2022,43(02):563-572.），建立三维基质—裂隙土柱模型，使用“空气单元”描述坡面积水水头。 使用VG模型和Brooks-Corey模型分别描述土基质和裂隙的非饱和特性，下图为0-5天内压力水头变化以及降雨断面入渗率以及参考文献对比）

最近在研究非饱和裂隙土降雨入渗相关课题，尝试复现侯晓萍和樊恒辉发表在《岩土力学》2022 年第 43 卷第 02 期的论文《基于 COMSOL Multiphysics 的非饱和裂隙土降雨入渗特性研究》。这过程可真是充满挑战与收获，和大家分享分享。

模型搭建：三维基质—裂隙土柱模型

在 Comsol 里构建三维基质—裂隙土柱模型，这可是关键的第一步。就像搭房子，模型结构搭不好，后续都是白搭。以 COMSOL 中的几何建模模块为例，我们可以通过以下类似代码（这里只是示意流程，非完整 Comsol 脚本）来逐步搭建：

# 假设我们在Python环境下调用Comsol相关接口（实际Comsol有自己的建模语法）
from comsol.model import Model
model = Model()
# 创建三维空间
model.geom.create('geom1', 3)
# 构建土柱主体
model.geom('geom1').feature.create('cylinder1', 'Cylinder')
model.geom('geom1').feature('cylinder1').set('radius', 0.5)
model.geom('geom1').feature('cylinder1').set('height', 1)
# 这里省略构建裂隙部分的复杂代码，实际构建裂隙需要更精细操作

在这段代码中，我们先初始化了一个 Comsol 模型实例，然后创建了三维几何空间，并在其中添加了一个圆柱体来初步代表土柱主体。当然，实际构建裂隙需要更复杂的几何操作与布尔运算，这里只是简单示意建模的流程思路。

“空气单元”描述坡面积水水头

用“空气单元”来描述坡面积水水头是这篇论文的一个巧妙之处。在 Comsol 的多物理场耦合设置中，我们可以通过如下方式（同样是示意性代码）来实现对空气单元相关属性设置，以模拟坡面积水水头：

# 假设已进入物理场设置模块
model.physics.create('spf1', 'Single - Phase Flow, Porous Media')
# 定义空气单元区域并设置相关属性
air_domain = model.geom('geom1').selection.create('air_domain', 'Domain')
air_domain.add(1) # 假设空气单元对应的区域编号为1
model.physics('spf1').bc.create('air_bc', 'Pressure')
model.physics('spf1').bc('air_bc').set('selection', air_domain)
model.physics('spf1').bc('air_bc').set('p', 0) # 设置压力边界条件为0，代表某种参考压力

这里，我们先创建了单相流多孔介质物理场，然后定义了空气单元所在区域，并为其设置了压力边界条件。这样就初步实现了利用“空气单元”来对坡面积水水头进行模拟的相关设置。

非饱和特性描述：VG 模型与 Brooks - Corey 模型

描述土基质和裂隙的非饱和特性分别使用 VG 模型和 Brooks - Corey 模型。这两个模型在 Comsol 中可以通过材料属性设置来实现。

VG 模型描述土基质非饱和特性

以 Comsol 材料属性设置界面来说，对应代码模拟如下：

model.materials.create('soil_matrix','Material')
model.materials('soil_matrix').property.create('permeability', 'Permeability')
model.materials('soil_matrix').property('permeability').set('model', 'Van Genuchten')
# 设置 VG 模型相关参数，如孔隙率、饱和渗透系数等
model.materials('soil_matrix').property('permeability').set('n', 1.5)
model.materials('soil_matrix').property('permeability').set('alpha', 0.01)
model.materials('soil_matrix').property('permeability').set('ks', 1e - 6)

在上述代码中，我们创建了名为“soil_matrix”的材料，并在其中设置渗透率模型为 Van Genuchten（即 VG 模型），同时设置了 VG 模型关键参数，像孔隙分布指数“n”、进气值倒数“alpha”以及饱和渗透系数“ks”。这些参数的设置直接影响到土基质非饱和特性的模拟效果。

Brooks - Corey 模型描述裂隙非饱和特性

同样地，对于裂隙部分使用 Brooks - Corey 模型设置如下：

model.materials.create('fracture', 'Material')
model.materials('fracture').property.create('permeability', 'Permeability')
model.materials('fracture').property('permeability').set('model', 'Brooks - Corey')
# 设置 Brooks - Corey 模型相关参数
model.materials('fracture').property('permeability').set('lambda_bc', 0.3)
model.materials('fracture').property('permeability').set('ks_fracture', 1e - 5)

这里我们创建了“fracture”材料，并将渗透率模型设置为 Brooks - Corey 模型，同时设定了 Brooks - Corey 模型特有的参数，如孔隙尺寸分布指数“lambdabc”和裂隙饱和渗透系数“ksfracture”。

模拟结果：0 - 5 天压力水头变化与降雨断面入渗率

经过一系列复杂的设置与计算，终于得到了 0 - 5 天内压力水头变化以及降雨断面入渗率的结果，并且和参考文献对比发现，整体趋势基本一致。这说明复现工作在一定程度上是成功的。

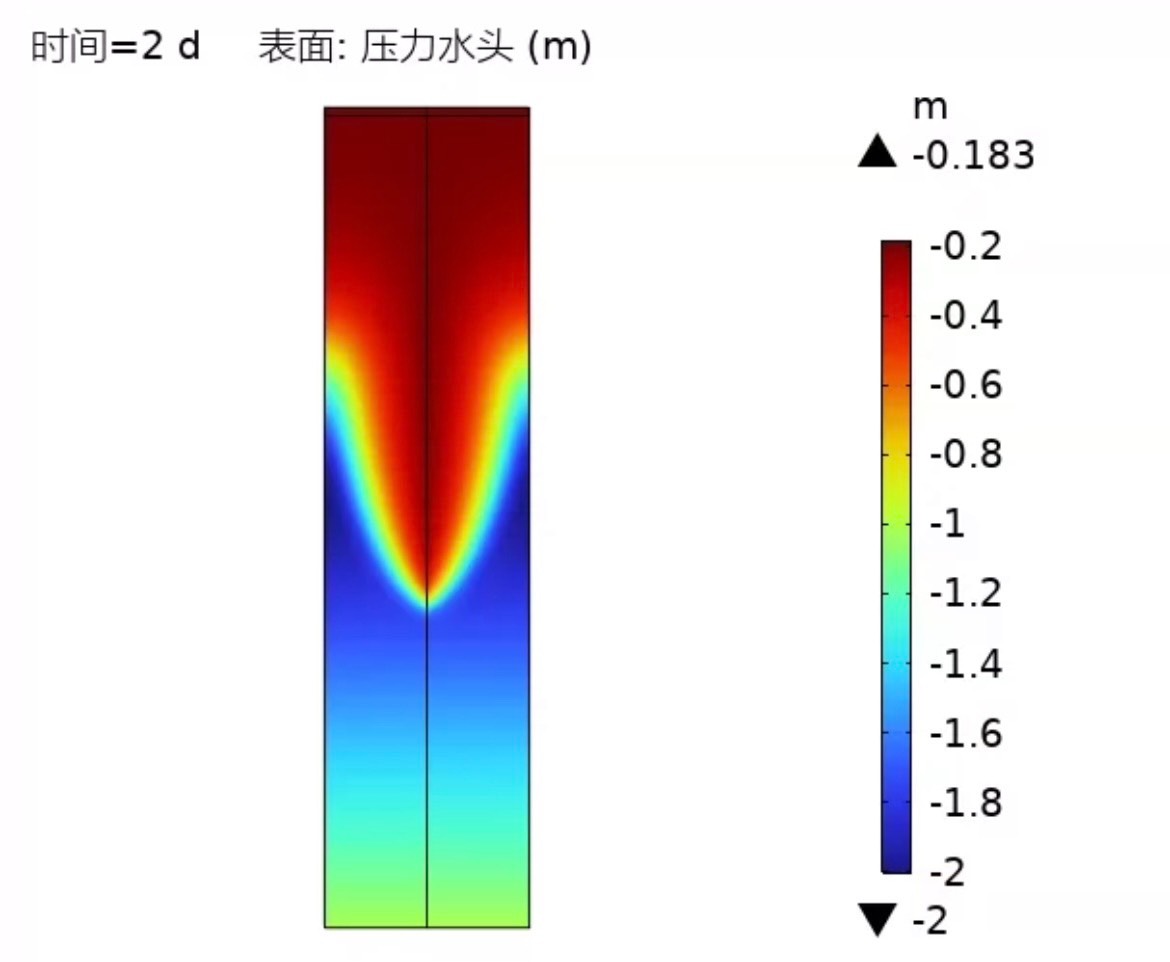
从压力水头变化图来看，随着降雨时间推进，土柱内部压力水头逐渐升高，特别是在靠近降雨面区域变化更为明显。而降雨断面入渗率在初期较高，随后随着土柱逐渐饱和，入渗率逐渐降低并趋于稳定。

这次复现过程不仅深入理解了非饱和裂隙土降雨入渗的物理机制，也对 Comsol 在这类复杂问题模拟上有了更熟练的掌握。希望这篇博文能给同样研究相关课题的小伙伴一些启发。

#参考文献

侯晓萍,樊恒辉.基于COMSOL Multiphysics的非饱和裂隙土降雨入渗特性研究[J].岩土力学,2022,43(02):563 - 572.