谐波平衡法：动力学方程求解的通用工具，适用于线性与非线性方程

谐波平衡法求解动力学方程。 线性非线性方程均可进行求解，。

弹簧振子突然开始蹦迪？这事儿在非线性动力学里还真有可能发生。今天咱们不聊数值积分那套老办法，直接上手谐波平衡法——这玩意儿处理周期响应就跟玩音游似的，能直接抓住振动节奏的命门。

先看个硬核例子：Duffing方程。这货长得像标准弹簧振子但自带叛逆属性：

def duffing_equation(x, t, alpha, beta, delta, gamma, omega):
    dx1 = x[1]
    dx2 = -delta*x[1] - alpha*x[0] - beta*x[0]**3 + gamma*np.cos(omega*t)
    return [dx1, dx2]

注意那个三次方项betax*3，这就是非线性的罪魁祸首。传统ODE解法在这会算到怀疑人生，特别是想找稳态周期解的时候。

谐波平衡法的骚操作在于直接假设解是傅里叶级数。比如我们猜解长这样：

N = 3  # 取到三次谐波
t = np.linspace(0, 2*np.pi, 100)
cos_terms = [np.cos(n*omega*t) for n in range(N+1)]
sin_terms = [np.sin(n*omega*t) for n in range(1, N+1)]

接下来把假设的解代入原方程，用最小二乘法逼着方程成立。实际操作时得构造一个超大的系数矩阵：

A = np.zeros((2*N+1, 2*N+1))
for i in range(2*N+1):
    for j in range(2*N+1):
        # 处理各阶谐波的交叉乘积项
        # 这里需要展开非线性项的谐波平衡关系
        ...

具体填矩阵元素时会发现非线性项引发的灾难——三次方项会产生交叉乘积项。这时候需要祭出三角恒等式大法，把cos³ωt拆成3cosωt/4 + cos3ωt/4这种形式。

当系数矩阵填完后，用最小二乘法求解：

coeffs = np.linalg.lstsq(A, F, rcond=None)[0]

解出来的系数直接对应各阶谐波的幅值。想看效果？对比数值积分结果：

from scipy.integrate import odeint
t = np.linspace(0, 100, 5000)
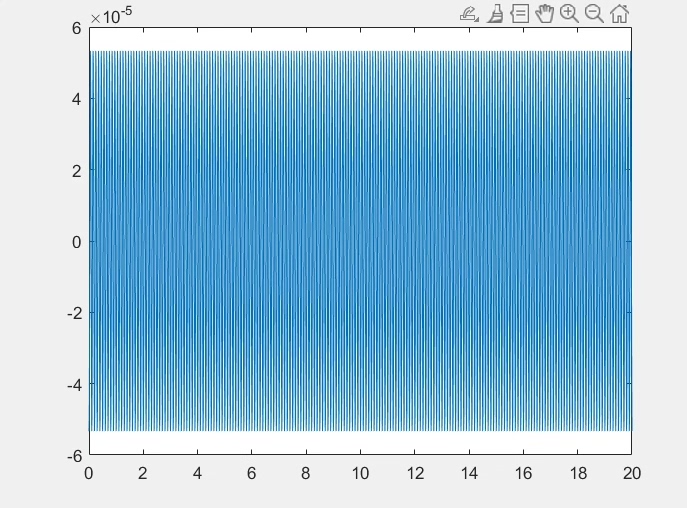
sol = odeint(duffing_equation, [0, 0], t, args=(1, 5, 0.2, 8, 1.2))

把谐波平衡解和数值解画在同一张图上，会发现前几个周期可能对不上——这很正常，谐波平衡法抓的是稳态解。等瞬态响应衰减后，两条曲线会完美重合。

重点来了：当遇到强非线性时（比如beta=100），传统的谐波平衡可能需要手动调参。试试把N设为5，然后在构造矩阵时处理五阶交叉项。这时候代码里会出现让人眼花缭乱的索引计算：

# 处理三次非线性项的三阶交叉
for m in range(-N, N+1):
    for n in range(-N, N+1):
        for p in range(-N, N+1):
            if m + n + p == k:
                # 计算对应项的系数贡献
                ...

这种时候就会明白为什么有些论文里的公式长得像外星文字——好在代码实现时可以用张量运算优化，不然嵌套循环能跑出咖啡凉。

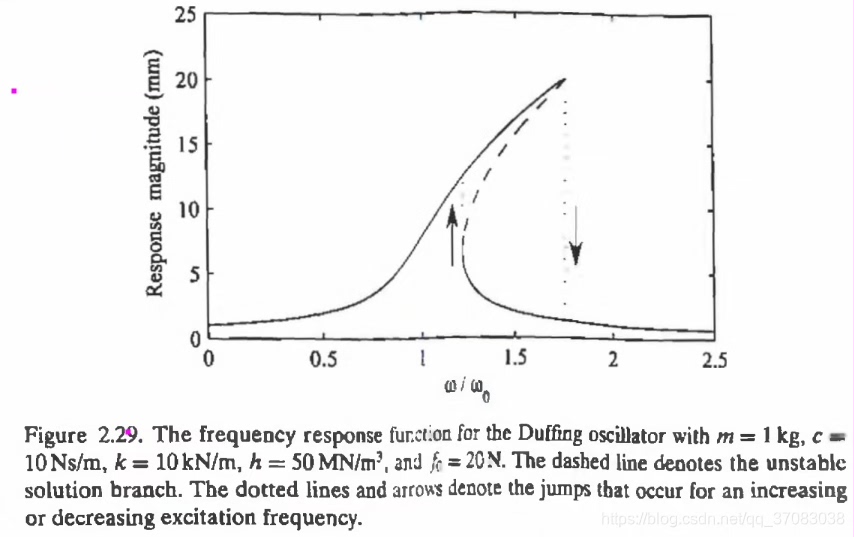
最后奉劝各位：虽然谐波平衡法能优雅地处理周期解，但碰到混沌系统还是得乖乖回去做数值积分。毕竟这方法的核心假设就是存在周期性稳态解，当系统本身不按套路出牌时，再优雅的数学技巧也得跪。