密集干扰下WiFi接收器演进

第1章 密集干扰环境下的WiFi接收器演进

帕特里克·托尔塔、安东尼奥·迪贾诺梅尼科、 卢卡斯·德尔勒和何塞·路易斯·塞瓦略斯

1.1 引言

接收链必须应对的最严苛场景是密集干扰环境，其中多个连续的接收信道被分配并由大量用户同时使用。在此类场景中，目标频带内需要转换的信号可能来自远距离站点，因此与近距离用户发射的信号相比可能非常微弱。

WiFi收发器可嵌入一个同时支持蜂窝通信、全球导航卫星系统、蓝牙或调频收音机等其他标准的共存运行平台。由于天线之间的隔离度通常仅限于约 10–12 dB，因此必须确保其他信号不会因混叠、折叠或失真而降低有用信号的质量。分析所有可能的干扰信号组合是一项复杂任务，特别是当模数转换时钟频率较低时，其倍数可能与接收链混频器时钟共同产生互调产物和折叠效应。

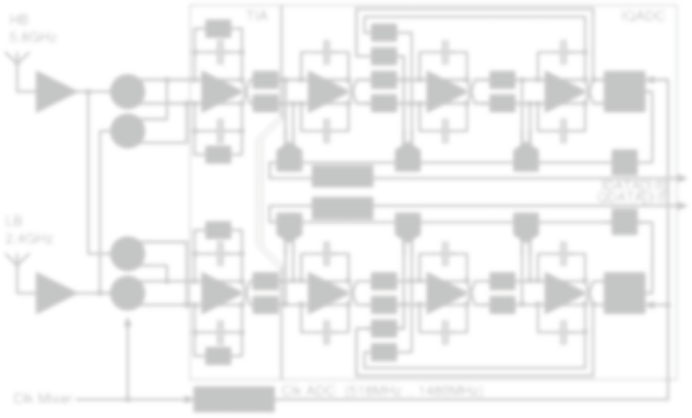
图1.1 滤波器和增益接收链以及ADC输入处的频谱

图1.1展示了一种基带频谱场景，以及由多个连续的滤波和增益级组成的接收链，后接一个中等分辨率模数转换器。该模数转换器以所需信号带宽奈奎斯特速率的两倍进行时钟采样。为了在ADC输入端提供足够的信噪失真比（SNDR），需要非常高的链路增益：这对接收链中的所有基带模块都提出了严格要求。特别是，该链路会显著放大混频器后级模块的非理想特性。

模拟有源器件的频率特性可能受到难以控制的寄生参数以及模块带宽和增益配置设置的显著影响。例如，混频器的直流偏移以及直接转换接收器的I‐Q 偏斜都需要被精确控制，并映射到所有链路配置以确保高链路分辨率。可能需要低噪声直流偏移消除。这导致复杂的增益和校准方案。

当使用过采样高分辨率模数转换器时，链路可以在吸收带外信号功率的同时保持所需的带内信噪失真比，并采用较低的链路增益。这放宽了某些模拟模块的要求以及所需数字校准的数量。

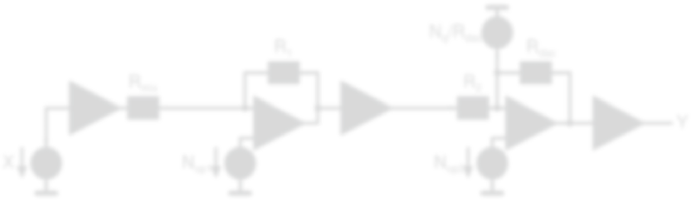
图1.2 本文提出的三种最小增益、高动态范围架构及其在基带中的典型功率谱密度图场景。带外信号未使链路饱和。由于时钟频率较高，实现了更少的带内折叠

图1.2中所示的接收机架构是实现高动态范围（DR）连续时间Σ‐Δ模数转换器（SD‐ADC）的最小化接收机架构。上方的架构在无源混频器与SD‐ADC之间仅实现了一个带有跨阻放大器（TIA）的有源滤波级。与滤波和增益链相比，该结构旨在最小化面积和功耗，并且对模块互连的电路非理想性更不敏感。它具有一个射频至基带接口，可通过常见的已知技术轻松进行仿真。为进一步减小面积和功耗，可省略 TIA级的实例化，如图1.2（中部）所示，通过一个小的无源衰减级和第一级中更低的极点来替代有源级。高阶SD‐ADC是一个混沌系统，通常无法直接使用谐波平衡法来仿真该链路性能，而可以采用线性化模型进行分析。所提出的两种低增益链路共同的特点是，混频器之后的第一个有源级由于射频链中的等效小阻抗而存在噪声增益问题。图（底部）中所示的第三种接收机架构采用电压模式下的无源混频器，后接一个具有高输出阻抗接口的跨导级（gm stage），连接至SD‐ADC。

1.2 将ReceiverChain作为功能齐全且公正的模数转换器验证环境

所有所述的接收机架构均能够转换两个Wi‐Fi射频频段中的信号。天线处的信号通过级联的差分低噪声放大器（LNA）进行放大，并下变频至零中频。一个无源开关位于与开关四相混频器级联的架构选择目标频带，信号随后被路由至I和Q基带路径。WiFi标准定义了可为每个用户分配包含不同数量子载波的信道。因此，所有提出的架构均能够处理带宽为8.9 MHz、18.3 MHz和38.3 MHz的基带信号。在模数转换器输出端，抽取链和数字滤波器对已转换的信号进行处理。

所实现的模拟增益控制根据模数转换器输出端检测到的信号强度，按比例调节低噪声放大器增益。在数字域中，还可以采集并存储未抽取的SD‐ADC数据流至内部存储器。除了有源极点之外，这些系统之间存在一个显著差异：ADC时钟可以由混频器本振(LO)产生，也可以由独立的锁相环提供。当有源模块缺乏隔离时，采用由本振产生的时钟尤为有利。在此情况下，需要在抽取链末端添加一个变速率转换器，将抽取后的采样插值到系统的固定频率。如果ADC使用系统时钟的倍数频率，则可省略变速率转换器。这三款芯片具有兼容引脚排列；特别是器件的编程、射频信号到低噪声放大器的走线以及电源线路的布局均相同，因此使用同一块母板对它们进行测量和比较。

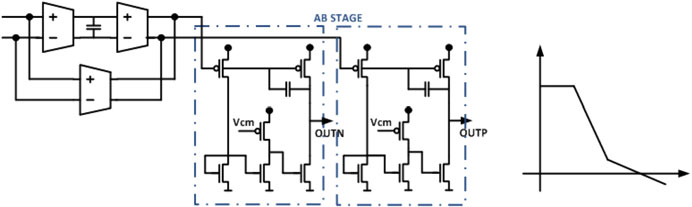
图1.3 包含抽取器和AGC的完整接收机中的时钟源

1.2.1 跨阻放大器-模数转换器架构

接收机的功能模块如图1.4所示。在此SD‐ADC以及其它所介绍的SD‐ADC中，所选的连续时间滤波器采用三阶反馈积分器链实现。该结构的一个优点是，TIA与ADC之间的电阻可编程，从而在增加增益复杂性的代价下，实现额外几dB的增益和动态范围提升。

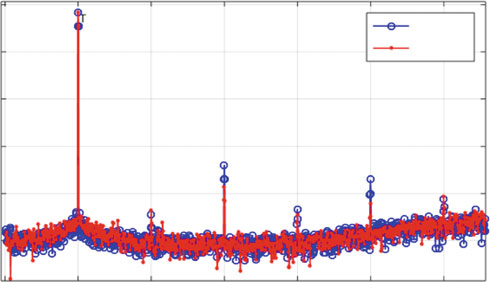
图1.4 首个提出的低增益高动态范围级联的概念图。跨阻放大器滤除高频信号

模块级噪声预算用于确定和设计各模块，其计算方法是将天线、LNA和混频器替换为一个高度简化的模型，如图1.5所示。该模型将天线替换为一个理想电压源，驱动一个值为G的无噪声电压增益元件，并连接至一个无噪声电阻Rmix，该电阻代表混频器的输出阻抗。该电阻值受所选射频前端架构的影响，在本设计中为几百欧姆。为进一步简化，基带中所有无源元件的噪声被忽略，因为放大器的噪声主导了总噪声，进而主导了系统面积和功耗。为了公平比较不同架构，我们假设所有系统中的G和Rmix均保持固定。TIA和ADC的传递函数（TF）在目标频带内是平坦的。因此，在噪声预算模型中，我们可以省略TIA电容以及ADC STF在带外的高频抑制。整个ADC因而简化为一个简单的反相放大器：反馈电阻Rdac是第一级电流舵DAC的等效电阻，它与电阻R2共同设定ADC增益。Nop1和Nop2模拟运算放大器折算到输入端的噪声，Nq则代表ADC的量化噪声。

我们可以利用叠加原理来计算系统在运算放大器增益非常高的假设下的折算到输入端的噪声。从输入X到输出Y的系统增益由以下公式给出：
$$
\frac{Y}{X} = \frac{R_{dac} R_1 G}{R_{mix} R_2}
$$

通过计算每个噪声源到输出的传递函数，并将其除以系统增益，我们得到输入参考噪声贡献方程：
$$
N^2_{input} = N^2_{op1} \left( \frac{R_1 + R_{mix}}{R_1 G} \right)^2 + N^2_{op2} \left( \frac{R_{dac} + R_2}{R_{mix}} \cdot \frac{R_{mix}}{R_{dac} R_1 G} \right)^2 + N^2_q \left( \frac{R_2 R_{mix}}{R_{dac} R_1 G} \right)^2
$$

量化噪声Nq的值由时钟驱动。一方面，为了降低功耗，需要尽量减小时钟频率；另一方面，较低的频率会降低DAC反馈的速率并减弱环路稳定性。由于相同的原因，ADC的极点也受到最高频率限制。由于量化噪声是在信号链末端加入的，因此可以通过增大R1和Rdac来提高增益，从而最小化该噪声。电源电压限制了第一级的总增益，并对ADC增益Rdac/R2设置了约束。因此，在两级结构中实现平坦传递函数且R2较小时，会对跨阻放大器噪声和ADC第一级噪声施加同等严格的限制。可以针对每个频率计算输入参考噪声预算，并结合数学工具求解系统方程，减少了简化步骤。分解的一个示例如图1.6所示。这两个模块的面积和功耗相当可观。

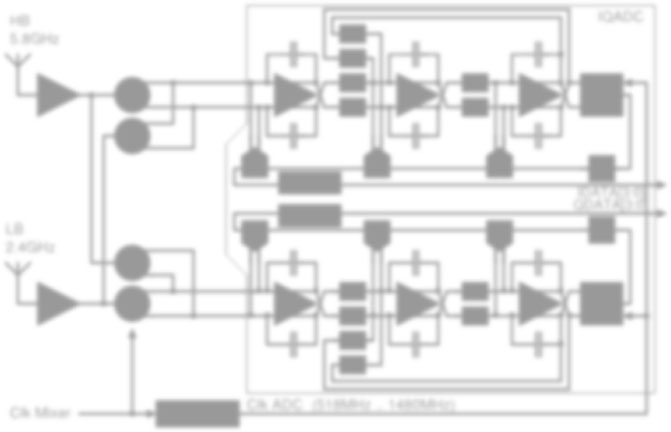
图1.5 跨阻放大器和模数转换器级联的简化直流噪声模型

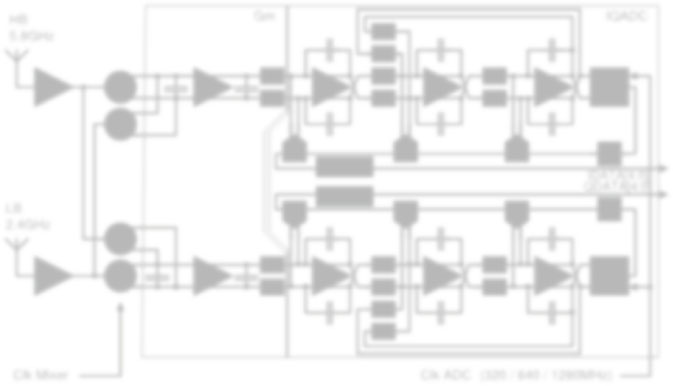
图1.6 链路增益和信号传递函数（上）以及输入参考噪声预算（下）。其中包括量化噪声、跨阻放大器以及第一级模数转换器运算放大器噪声的贡献。如果R2等于Rdac，则第一级运算放大器的噪声要求可大大放宽

为了将第一级的热噪声贡献降至最低，TIA级中采用了多路径运算放大器结构[1]。差分运算放大器概念如图1.7所示。通过编程gm级可以更好地权衡噪声（gm1和Cg1）、增益带宽积以及功耗之间的关系。两个级联的gm级能够在低频和中频实现非常高的增益。采用文献[2]中报道的AB类输出级的单级版本，以高效驱动积分器反馈电容和负载。设计中以下的运算放大器需要实现更高的带宽，但不需要太高的带内增益，因此采用了两级密勒补偿结构。

该产品线的时钟源自混频器时钟。本地振荡器(LO)通过一个随WiFi模式变化的整数因子进行分频。因此，时钟可以覆盖很宽的范围，模数转换器必须满足最低时钟下的所有稳定性和动态范围要求，同时还必须能够在最高时钟频率下运行。量化器与数模转换器之间的数据路径需要设计成在采样被DAC锁存器捕获时避免进入亚稳态区域。

图1.7 跨阻放大器与第一个模数转换器运算放大器采用GmC多路径结构，级联至AB类级（左）。运算放大器开环频率响应（右）

量化器设计实现了对[3]中提出的偏移补偿比较器的改进。基本差分比较器切片电路包括用于锁存器的参考电压生成电容网络和前置放大器，如图1.8所示。该电路主要在由ADC时钟驱动的两个不重叠相位下工作。在第一相位（如左侧所示），差分对的输出端和输入端被短接。所有比较器共用的参考满量程电压连接到比较器的电容阵列。通过这种方式，电容器中存储的电压相对于差分对的工作点进行采样。假设差分前置放大器增益为G，则在此工作条件下的输出电压为：
$$
V_{outdiff_ph1} = -G \frac{V_{Offs}}{G + 1}
$$

这意味着比较器的偏移电压$V_{Offs}$也被存储在电容器中。在第二阶段，如图1.8右侧所示，连接到SD‐ADC滤波器的开关关闭。这样，C1和C2之间发生电荷重分配。前置放大器输出端的电压由下式给出：
$$
V_{outdiff_ph2} = G \left( V_{indiff} + \frac{C_2 - C_1}{C_1 + C_2} V_{refdiff} - \frac{G V_{Offs}}{G + 1} \right) + V_{Offs}
$$

如果增益足够高，则最后两项会被抵消，偏移得到补偿。尽管电容器的总值可能仅为十分之几飞法，但该结构在第一阶段的速度受限于差分输入对上的寄生电容。因此，为该单元构建极度紧凑的布局至关重要。总寄生电容来源于布线路径上的寄生参数、差分对的栅极电容以及电阻负载相对于衬底表现出的寄生电容。

后一项的出现是由于在先进工艺中，电阻的最小宽度相比晶体管更宽。在这些工艺中，晶体管之间的允许最小间距比晶体管与多晶硅电阻之间的间距更短。为了缓解所有这些寄生效应，采用两个工作在欧姆区的长PMOS晶体管作为负载来替代电阻。由于该结构具有嵌入式偏移补偿，两个PMOS负载之间的失配无需担忧。另一个速度限制来自于第二阶段中的电荷重分配开关。与参考开关不同，输入开关所处的电位并不接近电源电压。问题在于$V_{inp}$和$V_{inn}$通常接近共模电压，这可以通过如图1.9所示实现的两种技巧来解决。

图1.8 量化器中比较器的参考电压和偏移采样相位（左），以及输入信号跟踪相位（右）

比较左右两部分：可使用三个升压开关sw代替两个，以降低其串联电阻Ron。此外，在比较器电平允许的情况下，可根据比例匹配和增益要求，将单位电容器Cu的数量减少到所需最小比例。

图1.9 包含四个比较器的完整量化器阵列（左），以及通过减少电容器数量实现更快电荷重分配的优化版本（右）。VINp开关可被升压以达到更高频率

量化器的输出在经过数百皮秒的微小延迟后被送入数模转换器。为了提高模数转换器的性能，数模转换器的传递函数应具有线性特性。由于DAC单元存在失配问题，已实现了后台校准。文献报道了多种线性化DAC的方法。采用动态元件匹配技术对单元进行随机化处理。

在仿真中效率很高，但由于环路中的额外延迟以及在第一个运算放大器输入端产生的共模毛刺能量，导致其难以直接实现。该毛刺会随着输入信号调制并产生失真音调。另一种线性化DAC的方法是校准单元的失配。可以通过数字控制方式对失配进行校准[4]，或者也可以在模拟环路内完成校准[5]。数字校准的优点是可观测性和操作在数字域中能得到良好控制，并且背景下的刷新频率可以较低；但其实现较为复杂，且残余误差受限于所实现的最低有效位。而模拟校准环路需要持续刷新，理论上能够将残余误差减小到很小的值。

在此模数转换器设计中，选择了模拟校准，因为这样可以降低复杂性。校准的电路思想如图1.10所示，该基本技术已知已久[6]。为了减少注入到积分器中的噪声量，未使用的DAC单元从滤波器断开并连接至一个浮动节点dump。如果某个单元正在使用，则来自量化器的数字字将被路由到开关DP x=DNx。模数转换器以非归零方式注入电流脉冲。电流导向PMOS和NMOS分为两部分：一部分宽幅晶体管连接至固定偏置电压，以提供约所需电流90%的电流。此外，并联的一个较小晶体管注入约10%的剩余校准电流，其偏置电压存储在本地电容中。当某个单元处于校准状态时，其量化器数据被路由至一个备用单元，该备用单元可接管向滤波积分器注入所需电流的任务。处于校准状态的单元会激活标有CALsw和DCx的开关。通过这种方式，参考电流单元被连接并与校准中的单元进行比较。由于参考单元和校准中的电流导向单元均具有高阻抗输出 (1/gds)，节点CALsw处的电压将稳定在产生参考电流所需的电压值。达到稳定后，该单元重新插入SD‐ADC环路中。由于单元的断开和重新插入可能影响存储的偏置电压，因此该操作以非重叠方式进行。

电路的功能已通过图1.11中的测量结果进行了测试，该电路能够通过降低三次谐波来线性化DAC。

图1.10 数模转换器的偏置以及一个包含用于操作、泄放和针对参考电流进行校准的开关的电流导向数模转换器单元

图1.11 测得的快速傅里叶变换频谱，通过注入一个−3dBFS音调并在有无校准的情况下进行。在校准后，三次谐波被抑制9dBFS

第1章 密集干扰环境中的WiFi接收器演进（续）

1.2.2 射频-ADC配置

线路结构如图1.12所示。如前一节所述，混频器与模数转换器之间存在有源级会加剧跨阻放大器和第一级模数转换器的噪声要求。该方案的思想是将跨阻放大器产生的噪声部分计入模数转换器的总噪声预算中，从而实际放宽其噪声要求。

图1.12 第二种提出的低增益高动态范围级联的概念示意图。SD‐ADC和混频器直接连接

根据图1.13的简化噪声模型，具有高增益放大器Ais的级联直流增益
$$
\frac{Y}{X} = \frac{R_{dac} G}{R_{mix}}
$$

以及输入噪声功率
$$
N^2_{input} = N^2_{op1} \left( \frac{R_{mix} + R_{dac}}{G R_{dac}} \right)^2 + N^2_q \left( \frac{R_{mix}}{G R_{dac}} \right)^2
$$

最终目标是减小整体面积和功耗。SD‐ADC的系数集需要满足带外信号抑制要求：这可以通过在ADC前端使用无源极点以及在第一级设置较低的截止频率来部分实现，从而限制量化噪声。这种架构的一个缺点是，若要改变 STF的低频增益，则需要重新编程DAC1电流以及第一级滤波电容器C1，或第二级输入电阻R2，以保持极点位置处于相同的频率。折算到输入端的噪声分解如图1.14所示。

该模数转换器的功能模块与先前的设计相同。混频器与模数转换器之间的接口需要特别注意。如果本振的时钟与第一级数模转换器的时钟不同步，杂散信号可能会污染带内频谱。数模转换器（DAC）充当差分电流源，但当单元状态发生变化时，仍不可避免地会产生微小的共模毛刺。该共模毛刺包含多个位于ADC时钟倍数频率处的谐波。混频器在相同频率下产生的差分信号被下变频至基带：其在数字ADC输出端的幅度取决于第一级性能，而该性能通常在较高频率下受限。在此架构中，时钟源自本振（LO），这使得对潜在问题场景的分析和评估更加容易。为了实现高频隔离，建议在ADC输入端添加一个较小且非主导的RC无源极点。过大的电容器会放大第一级噪声。

射频组件的设计需要基带电路的精确模型。由于ADC滤波器输出端的信号经过粗略量化，无法保证数据流具有周期性。Σ‐Δ ADC的这种非周期行为对所有基于谐波平衡的仿真器构成了阻碍。因此需要一个完整的晶体管级线性模型来模拟ADC。为此，可以将量化器和数模转换器替换为一个简单的压控电流源，如图1.15所示。该模型在较高的过采样率下能够很好地拟合实际的信号传递函数和噪声传递函数，并可用于验证整体链路性能。仿真与测量结果之间已实现了良好的匹配。在该模型中还可以模拟量化器的噪声贡献。

图1.13 射频ADC的简化直流噪声模型

图1.14 射频ADC的噪声预算分解。主要噪声产生于第一个运算放大器和量化器处

图1.15 SD‐ADC的线性化模型（上）及用于瞬态仿真的等效量化噪声发生器（下）

电阻产生的噪声可以根据由位数和ADC时钟频率确定的数值进行适当调整。实际模数转换器中的量化噪声在fclk处被采样，因此在其倍数处受到滤波。电阻的热噪声具有平坦的特性：因此建议在注入滤波器输出之前，使用LC滤波器对电阻噪声进行强滤波。

1.2.3 Gm-ADC架构

使时钟频率与本振同步可以简化对可能的阻塞场景的分析，但需要在数字域中使用变速率转换器，而这是一个高功耗模块。避免这一额外数字模块的一种方法是让SD‐ADC时钟与系统保持同步，并独立于本振。在这种架构中，非常重要的是在ADC STF级联之前实现一个强抗混叠功能，以避免混频器与数模转换器之间的互调。这通过在链路中引入一个gm级来实现。在所有提出的架构中，混频器都是无源的，由工作在共模电压下的简单开关组成。此时，混频器到基带接口并不固定在共模电压上，如同在电压域中的情况那样。这带来了一个机会——使用电容器对输入信号进行滤波。该gm单元以电流模式直接驱动模数转换器，在运算放大器输入端呈现为高阻抗输入负载Rg。与跨阻放大器链路相比，该gm级间结构放宽了第一级运算放大器的噪声预算要求。用于基本噪声预算计算的等效电路中不再包含混频器阻抗，仅保留低噪声放大器增益G（图1.16和图1.17）。

在假设为高增益放大器A的情况下，链路增益由以下公式给出：
$$
\frac{Y}{X} = \frac{G g_m R_g}{}
$$

且折算到输入端的噪声为
$$
N^2_{input} = N^2_{op1} \left( \frac{R_g + R_{dac}}{G g_m R_g R_{dac}} \right)^2 + N^2_g + N^2_q \left( \frac{1}{G g_m R_{dac}} \right)^2
$$

该gm cell噪声Ng相当显著，且在相同功耗条件下与跨阻放大器噪声处于同一量级。成形输入参考噪声分解如图1.18所示。该结构中的大部分节省来自更宏观的层面：如果实施了ADC前滤波，则可以将ADC的极点推向更高的频率。这允许降低ADC时钟或降低折算到输入端的量化噪声Nq。降低ADC时钟并省去数字抽取链末端的变速率转换器，可在总功耗方面实现显著节省：这一权衡是有利的，因此采用5位量化器以进一步支持该设计。

当差分峰峰值输入在几百mV范围内时，gm单元能够提供线性输出。增益级之后的电压接口会暴露并放大任何先前存在的失配。无源混频器以及无源混频器到Gm输入之间的路径必须仔细检查，并确保I路和Q路之间良好匹配。因此，该接口提供了在输入端添加极点的机会，但由于后续会放大失配，且没有进一步的数字IQ失配校准，该极点不能作为主导极点。可以在gm输出端添加一个电容器和一个串联电阻，以构建一个gmC低通滤波器，从而减轻 SD‐ADC第一级的压力。然而，该极点的频率不能设置过低，否则电容器将影响第一级运算放大器的反馈系数。

图1.16 第三种提出的低增益高动态范围级联的概念示意图。跨导级在输入端和输出端通过电容器滤除带外信号

图1.17 跨导放大器模数转换器的简化直流噪声模型

图1.18 信号传递函数（上图）和输入参考噪声预算（下图）。跨导单元噪声与量化噪声共同构成了主要的噪声来源

1.3 测量结果

采用28纳米CMOS工艺制造了三款测试芯片以实现所述架构，从而直接比较结果。在天线上施加了WiFi OFDM模式，并在主要模式下测得的EVM性能如图1.19所示。在图1.20中展示了该EVM模式的一个示例。正如预期，性能相当，从而可以公平地比较表1.1中报告的其余关键参数以及GmADC的芯片显微照片。

图1.19 通过增加输入信号功率对三种模式下三款阵容的误差矢量幅度进行比较

图1.20 在80兆赫带宽下采用256正交幅度调制VHT80信号模式的射频ADC产品线性能

Parameter	TIA-ADC	RFADC	GmADC
Clock frequency (MHz)	518–720 (W20) 1036–1280	518–720 (W20) 1036–1280	320 (W20) 640 (W40) 1280 (W80)
Total current consumption for the BB blocks in WiFi20/40/80 (mA)	16 / 20 / 23	11 / 15 / 19	11 / 16 / 17 (w/o digital)
Max EVM in WiFi20/40/80 (dB)	33.4 / 31.8 / 33.0	35.0 / 35.2 / 35.7	34.9 / 36.1 / 35.8
Area compared to TIAADC (%)	100	61	72
Supply (V)	1.1	1.1	1.1
Technology (nm)	28	28	28

1.4 结论

所提出的低增益接收机架构利用高动态范围Σ‐Δ ADC，以减少模块数量、面积和功耗。如果需要优化面积，则应优先选择RFADC架构。在带外抑制和功耗方面，GmADC更优，因其降低且固定的时钟频率可在数字域实现显著的功耗节省。