CSP-J 2025 第二轮 T2 座位 / seat 详细解析

最新推荐文章于 2025-12-15 22:32:00 发布

原创最新推荐文章于 2025-12-15 22:32:00 发布 · 970 阅读

9 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #c++ #数据结构 #GESP #信奥赛

CSP-J入门组第二轮题目详解专栏收录该内容

8 篇文章

订阅专栏

P14358 [CSP-J 2025] 座位 / seat（官方数据）

题目描述

CSP-J 2025 第二轮正在进行。小 R 所在的考场共有 $\times m$ 名考生，其中所有考生的 CSP-J 2025 第一轮成绩互不相同。所有 $\times m$ 名考生将按照 CSP-J 2025 第一轮的成绩，由高到低蛇形分配座位，排列成 $n$ 行 $m$ 列。具体地，设小 R 所在的考场的所有考生的成绩从高到低分别为 $s1>s2>⋯>sn×ms_1 > s_2 > \dots > s_{n \times m}$ ，则成绩为 $s_1$ 的考生的座位为第 1 列第 $1$ 行，成绩为 $s_2$ 的考生的座位为第 $1$ 列第 $2$ 行， $…\dots$ ，成绩为 $s_n$ 的考生的座位为第 $1$ 列第 $n$ 行，成绩为 $s_{n+1}$ 的考生的座位为第 $2$ 列第 $n$ 行， $…\dots$ ，成绩为 $s_{2n}$ 的考生的座位为第 $2$ 列第 $1$ 行，成绩为 $s_{2n+1}$ 的考生的座位为第 $3$ 列第 $1$ 行，以此类推。

例如，若 $n = 4, m = 5$ ，则所有 $\times 5 = 20$ 名考生将按照 CSP-J 2025 第一轮成绩从高到低的顺序，根据下图中的箭头顺序分配座位。

:::align{center}

:::

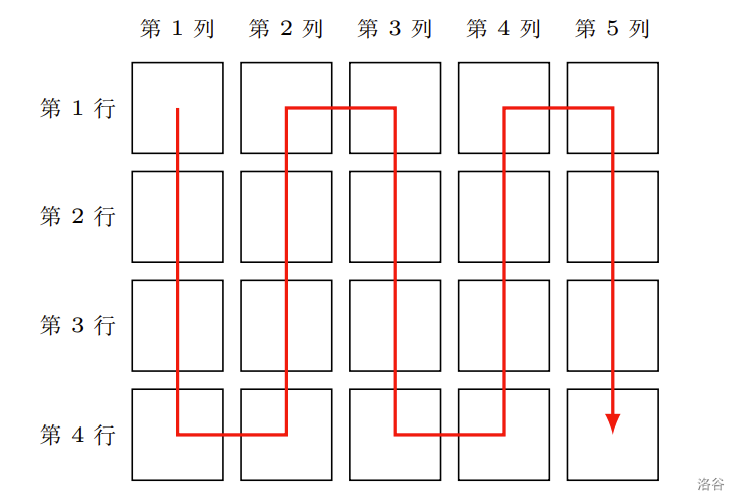
给定小 R 所在的考场座位的行数 $n$ 与列数 $m$ ，以及小 R 所在的考场的所有考生 CSP-J 2025 第一轮的成绩 $a1,a2,…,an×ma_1, a_2, \dots, a_{n \times m}$ ，其中 $a_1$ 为小 R CSP-J 2025 第一轮的成绩，你需要帮助小 R 求出，他的座位为第几列第几行。

输入格式

输入的第一行包含两个正整数 $n, m$ ，分别表示小 R 所在的考场座位的行数与列数。

输入的第二行包含 $\times m$ 个正整数 $a1,a2,…,an×ma_1, a_2, \dots, a_{n \times m}$ ，分别表示小 R 所在的考场的所有考生 CSP-J 2025 第一轮的成绩，其中 $a_1$ 为小 R CSP-J 2025 第一轮的成绩。

输出格式

输出一行两个正整数 $c, r$ ，表示小 R 的座位为第 $c$ 列第 $r$ 行。

输入输出样例 #1

输入 #1

2 2
99 100 97 98

输出 #1

1 2

输入输出样例 #2

输入 #2

2 2
98 99 100 97

输出 #2

2 2

输入输出样例 #3

输入 #3

3 3
94 95 96 97 98 99 100 93 92

输出 #3

3 1

说明/提示

【样例 1 解释】

按照成绩从高到低的顺序，成绩为 $100$ 的考生的座位为第 $1$ 列第 $1$ 行，成绩为 $99$ 的考生的座位为第 $1$ 列第 $2$ 行，成绩为 $98$ 的考生的座位为第 $2$ 列第 $2$ 行，成绩为 $97$ 的考生的座位为第 $2$ 列第 $1$ 行。小 R 的成绩为 $99$ ，因此座位为第 $1$ 列第 $2$ 行。

【样例 2 解释】

按照成绩从高到低的顺序，成绩为 $100$ 的考生的座位为第 $1$ 列第 $1$ 行，成绩为 $99$ 的考生的座位为第 $1$ 列第 $2$ 行，成绩为 $98$ 的考生的座位为第 $2$ 列第 $2$ 行，成绩为 $97$ 的考生的座位为第 $2$ 列第 $1$ 行。小 R 的成绩为 $98$ ，因此座位为第 $2$ 列第 $2$ 行。

【数据范围】

对于所有测试数据，保证：

$\leq n \leq 10$ , $\leq m \leq 10$ ;
对于所有 $\leq i \leq n \times m$ ，均有 $\leq a_i \leq 100$ ，且 $a1,a2,…,an×ma_1, a_2, \dots, a_{n \times m}$ 互不相同。

::cute-table{tuack}

测试点编号	$\leq$	$\leq$	特殊性质
$1$	$1$	$1$	AB
$2, 3$	^	$10$	无
$4, 5$	$10$	$1$	^
$6$	$2$	$2$	A
$7$	^	^	B
$8, 9$	^	^	无
$10$	^	$10$	A
$11$	^	^	B
$\sim 14$	^	^	无
$\sim 17$	$10$	$2$	^
$\sim 20$	^	$10$	^

特殊性质 A：对于所有 $\leq i \leq n \times m$ ，均有 $a_i = i$ 。

特殊性质 B：对于所有 $\leq i \leq n \times m$ ，均有 $ai=n×m−i+1a_i = n \times m - i + 1$ 。

【模拟算法解题思路】

模拟算法解决这个问题，我们可以按照蛇形规则构建一个二维数组来表示座位分布，然后通过遍历数组找到小R的位置。具体步骤如下：

解题思路

获取输入并确定小R的成绩：读取考场的行数n、列数m，以及所有考生的成绩，其中第一个成绩是小R的成绩。
排序成绩：将所有成绩从高到低排序，因为座位是按成绩从高到低分配的。
模拟蛇形填充座位：按照蛇形规则（奇数列从上到下，偶数列从下到上），将排序后的成绩依次填入一个二维数组中，数组的行和列对应实际座位的行和列。
查找小R的位置：遍历填充好的二维数组，找到小R成绩所在的位置，输出对应的列号和行号。

C++实现代码

#include <iostream>
#include <algorithm>
using namespace std;

int main() {
    int n, m; // n行m列
    cin >> n >> m;
    int t = n * m; // 总人数
    int s[100]; // 存储所有成绩（最大10*10=100）
    for (int i = 0; i < t; ++i) {
        cin >> s[i];
    }
    int rs = s[0]; // 小R的成绩

    // 对成绩从高到低排序，存到ss数组
    int ss[100];
    for (int i = 0; i < t; ++i) ss[i] = s[i];
    sort(ss, ss + t, greater<int>());

    // 座位数组（m列n行，0-based索引）
    int seat[10][10]; // 最大10x10，满足题目范围

    // 按蛇形规则填充座位
    for (int c = 0; c < m; ++c) { // 遍历每一列（0-based）
        int ac = c + 1; // 实际列号（1-based）
        int si = c * n; // 该列在排序后数组中的起始索引
        for (int k = 0; k < n; ++k) { // 处理列中第k个元素
            int sc = ss[si + k]; // 当前要放置的成绩
            int r; // 行索引（0-based）
            if (ac % 2 == 1) { // 奇数列：从上到下（行号递增）
                r = k;
            } else { // 偶数列：从下到上（行号递减）
                r = n - 1 - k;
            }
            seat[c][r] = sc; // 放入座位
        }
    }

    // 查找小R的座位（转换为1-based输出）
    int rc, rr;
    for (int c = 0; c < m; ++c) {
        for (int r = 0; r < n; ++r) {
            if (seat[c][r] == rs) {
                rc = c + 1;
                rr = r + 1;
                break;
            }
        }
    }

    cout << rc << " " << rr << endl;
    return 0;
}

代码说明

输入处理：读取行数n、列数m和所有考生的成绩，其中第一个成绩是小R的成绩。
成绩排序：将成绩从高到低排序，因为座位分配顺序是按成绩从高到低进行的。
蛇形填充：创建一个m列n行的二维数组，按列填充：
- 奇数列（1-based）从上到下填充（行号从1到n）。
- 偶数列（1-based）从下到上填充（行号从n到1）。
查找位置：遍历二维数组，找到小R成绩所在的位置，转换为1-based索引后输出列号和行号。

【数学规律解题思路】

思路分析

核心思想

蛇形排列规则：
- 奇数列：从上到下填充
- 偶数列：从下到上填充
- 按成绩从高到低依次分配座位
关键步骤：
- 确定小R在所有考生中的排名
- 根据排名计算对应的行列位置
- 考虑蛇形排列的特殊性

算法流程

统计比小R成绩好的人数，确定小R的排名
计算列号：(排名-1) / 行数 + 1
计算行号：根据列号的奇偶性决定计算方式

C++代码实现

#include <iostream>
using namespace std;

int main() {
    int n, m;  // 行数, 列数
    cin >> n >> m;
    
    int sz = n * m;  // 总人数
    int a[sz];       // 成绩数组
    
    // 读入成绩
    for (int i = 0; i < sz; i++) {
        cin >> a[i];
    }
    
    int rScore = a[0];  // 小R的成绩
    int cnt = 0;        // 比小R成绩好的人数
    
    // 统计比小R成绩好的人数
    for (int i = 0; i < sz; i++) {
        if (a[i] > rScore) {
            cnt++;
        }
    }
    
    int rk = cnt + 1;  // 小R的排名（从1开始）
    
    // 计算列号：每列n个人，从0开始计算
    int c = (rk - 1) / n + 1;
    
    // 计算行号
    int r;
    if (c % 2 == 1) {  // 奇数列：从上到下
        r = (rk - 1) % n + 1;
    } else {           // 偶数列：从下到上  
        r = n - (rk - 1) % n;
    }
    
    cout << c << " " << r << endl;
    return 0;
}

输入输出样例分析

样例1分析

输入: 2 2
      99 100 97 98
输出: 1 2

成绩排序：100(1), 99(2), 98(3), 97(4)
小R成绩99，排名第2
第2个位置：第1列第2行（奇数列从上到下）

样例2分析

输入: 2 2
      98 99 100 97
输出: 2 2

成绩排序：100(1), 99(2), 98(3), 97(4)
小R成绩98，排名第3
第3个位置：第2列第2行（偶数列从下到上）

样例3分析

输入: 3 3
      94 95 96 97 98 99 100 93 92
输出: 3 1

小R成绩94，排名第7
第7个位置：第3列第1行（奇数列从上到下）

关键点总结

排名计算：统计比小R成绩好的人数 + 1
列计算：(排名-1)/行数 + 1（整数除法）
行计算：根据列号奇偶性采用不同计算方法
边界处理：注意数组索引从0开始，排名从1开始