追逐最远邻居的聚集算法

追逐最远的邻居

一种用于匿名、无记忆且不通信智能体的简单聚集算法

罗特姆·马诺尔和阿尔弗雷德·M·布鲁克斯坦

1 引言

最近，人们开始关注使用极简机器人智能体的群体来执行各种任务。这些简单的机器人仅具备基本感知、运动和计算能力。事实证明，即使智能体是无记忆的，且仅具有基本数据处理技能和有限感知能力，也可以被编程以完成若干有用的任务，研究这类智能体所能实现的功能既有趣又极具挑战性。该课题已获得大量研究关注，并产生了丰富的研究成果。贾德巴拜和莫罗及其合作者（参见例如 [11, 13]），研究了相互连接间歇性存在的网络化智能体，并证明只要随时间发生足够多的交互，就能确保实现集群与聚集。铃木和山下（[15]），提出了在有限感知和计算能力条件下聚集智能体的几种有趣算法，其中引人注目的是“追逐最远邻居”过程。莫罗在 [14] 中证明，若智能体始终位于其当前凸包内部移动，则可保证收敛。

本文讨论了连续时间和离散时间下的多智能体聚集问题，表明通过应用一种非常简单的运动定律，执行“追逐最远邻居”策略，一群简单智能体可以在有限期望时间内聚集到一点。铃木和山下在其论文 [15] 的早期版本中，针对 R² 平面上具有无记忆、匿名和无限视野特性的离散时间多智能体系统，提出了一种实现点收敛的算法。他们还在论文中证明，如果智能体无法就一个共同的会合点达成一致，则不可能在有限的时间步数内完成该任务。

我们首先在连续时间框架下分析一个类似的算法，用于智能体具有有限视野或感知能力的情况。在离散情况下，我们提出一种基于相同“追逐最远者”思想的随机算法，该算法可在有限的期望时间步数内完成聚集任务。

本文首先讨论了一些基本概念，然后在连续时间框架下研究具有无限视野和有限视野的智能体向一点聚集的问题。接着讨论了在离散时间框架下实施“追逐最远邻居”策略时出现的问题，表明具有无限视野的智能体系统会聚集成一个小区域。最后证明，在无限视野和有限视野条件下，以及智能体运动采用随机半同步时序的情况下，系统能够在有限期望时间内实现向一点聚集。

2 预备知识

我们研究一个由 n 个相同且匿名的无记忆智能体组成的系统，这些智能体位于 R² 平面中，其位置由时变位置 {pi(t)}i=1,2,…,n 表示。智能体之间通过相互作用来更新自身的位置，其位置更新取决于自身的当前位置以及与其邻居的交互。在时刻 t，每个智能体 i 的邻居定义为位于其给定可视范围 V 内的其他智能体集合，即相对于位置 pi(t) 距离不超过 V 的所有智能体，该集合记为 Ni(t)。智能体之间的邻接关系由一个随时间变化的可见性图描述。需要注意的是，当考虑无限视野时，集合 Ni(t) 包含除智能体 i 之外的所有智能体，此时可见性图为完全图，即所有智能体彼此“可见”。

本论文提供了对在平面中建模为点的智能体群体采用“追逐最远邻居”运动规则进行聚集的证明。假设机器人可以在连续时间下相互穿越路径而无障碍，在连续时间情况下不存在决策或计算引起的延迟；而在离散情况下，我们假设采用同步或半同步的概率运动调度。

请注意，本文仅介绍了定理证明的核心内容。完整的证明可在 [12] 中找到。

3 连续时间聚集

3.1 无限视野

“追逐最远者”聚集规则的核心思想是：每个智能体持续向其当前最远邻居的位置移动。如果有多个邻居与其距离相同且均为最远距离，该智能体将任意选择其中一个最远邻居，并向其位置移动。这一动态规则十分简单，我们将证明，若系统中所有智能体均遵循此规则，则系统最终会聚集到一点。

为了定义一个形式化的动态规则，我们考虑最远的智能体（邻居）的集合。设 $N^{\text{Far}}_i(t) \subset N_i(t)$ 为在时刻 t 距离智能体 i 最远的智能体的集合。
$$
j \in N^{\text{Far}}_i(t) \iff \forall q \in N_i(t), |p_i(t) - p_j(t)| \geq |p_i(t) - p_q(t)|
$$

智能体的正式动态规则是：每个智能体以恒定速度 $\sigma > 0$ 朝集合 $N^{\text{Far}}_i(t)$ 中某个任意智能体 j 的位置移动，除非其已与 j 共处一地（此时，智能体们无记忆地全部聚集！）。
$$
\dot{p}_i(t) =
\begin{cases}
\sigma \frac{p_j(t) - p_i(t)}{|p_j(t) - p_i(t)|}, & |p_j(t) - p_i(t)| > 0, j \in N^{\text{Far}}_i(t) \
0, & \text{o.w.}
\end{cases}
\quad (1)
$$

注意，在 (1) 中，j 是集合 $N^{\text{Far}}_i(t)$ 中的任意一个智能体。因此，这里的一个关键问题是需要持续地从可能包含多个智能体的集合 $N_i(t)$ 中选择最远邻居（这使得有必要评估速度控制规则 $\dot{p}_i(t)$ 的适定性，因为原则上在选择 i 时可能发生无限次切换）。然而，可以认为所有选择对 $p_i(t)$ 的影响是类似的，并且可以使用单调性论证来证明演化过程的适定性，并对智能体间距离的变化速率给出正确的界。有关类似问题的讨论，请参见 [4, 5]。

定理 1 一个具有动态规则 (1) 的 n 个智能体系统将在有限时间内聚集到一点。
该证明基于对系统智能体凸包的当前直径 $D(P(t))$ 的变化率的分析，即
$$
D(P(t)) = \max_{i,j} |p_i(t) - p_j(t)|
$$
我们证明了位于直径边缘的每个智能体，其速度在指向该直径另一边缘的方向上的投影严格为正，且至少为 $\sigma \cos(\pi/3)$。因此，该系统将聚集到有限时间内的一点 $D(P(0))/\sigma$，证明定理 1（完整证明见 [12] 定理 1）。

3.2 有限可见性

在本节中，我们将“追逐最远者”这一概念应用于具有有限视野的智能体。
假设每个智能体仅能感知位于其可视范围 V 内的其他智能体。显然我们无法使用之前的算法，因为在移动过程中智能体可能会与其邻居失去可见性，从而形成不连通组。例如，假设一个智能体有两个邻居，二者均位于距离它 V 的位置，且指向这两个邻居的向量之间的夹角大于 $\pi/2$。那么，朝其中一个邻居移动将导致与另一个邻居失去可见性。

该问题的解决方案由一个略微复杂的算法给出。我们提出了一种新的动态规则，能够解决连通性问题，并在有限时间内使系统聚集到一点。该算法仍然基于“追逐最远者”的概念，与之前的动态规则类似，但在智能体根据所考虑的运动定律感知到多个最远邻居时，它不会远离其中任何一个。

形式化动态规则的表述要求我们调整某些定义。设 $N^{\text{Far}}_i(t) \subset N_i(t)$ 为智能体 i 的最远可见邻居子集，即集合 $N^{\text{Far}}_i(t)$ 中所有智能体到 i 的距离均相等，而集合 $N_i(t)$ 中的其他智能体距离 i 更近。

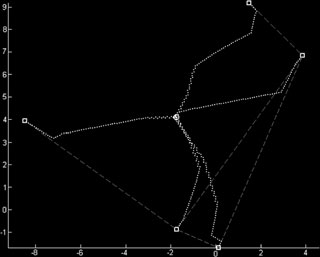
每个智能体 i 持续计算 $\psi^{\text{Far}}_i(t)$，即以 $p_i(t)$ 为锚点并包含其最远邻居 $N^{\text{Far}}_i(t)$ 的最小圆盘扇区的角度。如果 $\psi^{\text{Far}}_i(t)$ 大于或等于 $\pi$（即智能体 i 被其最远邻居“包围”），则该智能体保持静止。否则，它以速度 $\sigma > 0$ 沿 $\hat{U}^{\text{Far}}_i(t)$ 方向移动，其中 $\hat{U}^{\text{Far}}_i(t)$ 是角 $\psi^{\text{Far}}_i$ 的角平分线方向上的单位向量（见图1）。

因此，智能体 i 的运动定律为
$$
\dot{p}_i(t) =
\begin{cases}
\sigma \hat{U}^{\text{Far}}_i(t), & \psi^{\text{Far}}_i(t) < \pi \
0, & \psi^{\text{Far}}_i(t) \geq \pi
\end{cases}
\quad (2)
$$

请注意，大多数情况下，一个智能体只有一个最远邻居，此时 $\psi^{\text{Far}}_i = 0$，且智能体 i 向其唯一的最远邻居移动（见图1a）。

在证明收敛性之前，我们首先说明运动定律（2）能够保持系统可见性图的连通性，即如果系统中的所有智能体都遵循该定律，则它们将维持与当前所有邻居的可见性。

引理 1 运动定律（2）确保初始构型中的邻居将永远保持为邻居。

证明 设 {i,j} 为一对邻居。为了使该对在可见性图中断开，$l_{ij}(t)$（即这些智能体之间的距离）必须超过 V。在此状态下，i 和 j 必然互为最远邻居，因为它们均无法感知超出 V 范围的其他智能体，即
$$
|p_i(t) - p_j(t)| = V \Rightarrow j \in N^{\text{Far}} i(t) \text{ and } i \in N^{\text{Far}}_j(t)
$$
根据运动规则 (2)，对于智能体 i，如果 $\psi^{\text{Far}}_i(t) \geq \pi$，则它保持静止。否则（如果 $\psi^{\text{Far}}_i(t) < \pi$），它将以速度 $\sigma$ 沿方向 $\hat{U}^{\text{Far}}_i(t)$ 移动。因此，如果智能体没有保持静止，则其移动方向与指向智能体 $j \in N^{\text{Far}}_i$ 的方向之间的夹角小于或等于 $\pi/2$。记该角度为 $\theta {ij}(t)$。然后考虑一对 {i, j}，其中 $j \in N^{\text{Far}} i(t)$ 且 $i \in N^{\text{Far}}_j(t)$，我们有
$$
\dot{l} {ij}(t) = \frac{p_i(t) - p_j(t)}{|p_i(t) - p_j(t)|}^\top (\dot{p} i(t) - \dot{p}_j(t)) = -(|\dot{p}_i(t)| \cos(\theta {ij}(t)) + |\dot{p} j(t)| \cos(\theta {ji}(t))) \leq 0
$$
表明当 i 和 j 到达 V 后，它们之间的距离不会增加，因此不可能超过 V。这证明了该引理。

请注意，该系统的智能体无需“知晓”其可视范围 V 即可避免丢失邻居，但我们需要确保所有智能体具有相同的可视范围（这一点由我们假设所有智能体都相同来保证）。

定理 2 一个由 n 个智能体组成的系统，若按照运动规则（2）移动，且具有连通的初始可见性图，则将在有限时间内聚集到一点。
该定理的证明基于考虑位于系统凸包当前最尖锐角落处的智能体 s 的动力学行为，根据引理 1，该智能体在任何时刻至少需连接另一个智能体。设 $\phi_s(t)$ 为该角落的内角，根据 [12] 中的命题 2，该内角存在上界由 $\phi^ = \pi(1 - 2/n)$ 得出。因此，$\psi^{\text{Far}}_s(t) \leq \phi^ $，且智能体 s 必然以速度 $\sigma > 0$ 在系统凸包内部移动，而根据运动定律 (2)，显然其他任何智能体都无法移出该凸包。

因此，$l_{CH}(t)$，即该系统凸包的周长，只要其长度不为零，就会以一个远离零的恒定速率持续下降，如下所示：
$$
\dot{l}_{CH}(t) \leq -2\sigma \cos^2\left(\frac{\phi^*(t)}{2}\right)
$$
因此，该系统会在有限时间内聚集到一点，正如定理 2 中所声称的（见图2中的定理2的完整证明）。展示了 5 个智能体从连通的可见性网络的构型开始，最终聚集到一点的仿真结果。请注意，智能体速度的不连续性是动态规则导致突然切换事件的结果，这是由于它们的最远邻居（和/或它们对最远邻居的选择）发生变化所致。

追逐最远的邻居

一种用于匿名、无记忆且不通信智能体的简单聚集算法

罗特姆·马诺尔和阿尔弗雷德·M·布鲁克斯坦

4 离散时间“追逐最远者”聚集

下文我们将分析离散时间框架下的“追逐最远邻居”概念。首先，我们证明：在具有无限视野的一组智能体中，若采用步长为 $\sigma > 0$ 的“追逐最远”算法，则这些智能体会聚集到一个半径为 $\sigma$ 的圆盘内。我们通过一种非常规的几何李雅普诺夫函数来证明这一点。接着，我们进一步证明，在半同步模型中，只要智能体能够以小于或等于 $\sigma$ 的步长移动，该群体便能在有限期望步数内聚集到一点。本节最后，我们指出，只需对智能体的步长施加一个简单的约束，即使智能体具有有限视野，也能确保其聚集。

4.1 无限视野

我们接下来假设每个智能体 $i$ 向集合 $N^{\text{Far}}_i(k)$ 中任意一个智能体的位置跳跃一个大小为 $\sigma$ 的步长：
$$
p_i(k+1) = p_i(k) + \sigma \frac{p_j(k) - p_i(k)}{|p_j(k) - p_i(k)|}, \quad \text{其中 } j \text{ 是集合 } N^{\text{Far}}_i(k) \text{ 中的任意智能体} \quad (3)
$$

运动规则（3）不会将系统聚集到一个点（除了某些特殊情况，即智能体的初始构型导致它们在同一时间步恰好跳到同一位置），因为当系统中的智能体处于近距离时，它们可能会相互越过。尽管如此，我们证明系统的动态行为会在 $\mathbb{R}^2$ 有限的时间步内将所有智能体带到一个小的有界区域内。

定理 3 在动态规则（3）下，由 $n$ 个智能体组成的系统将在有限的时间步内聚集到半径为 $\sigma$ 的圆盘中。
该定理的证明基于对智能体最小包围圆半径变化率的分析。根据几何学，每个智能体的最远邻居位于最小包围圆中心 $C(k)$ 之外的区域，如图3所示。

因此，如果 $C(k)$ 与某一智能体当前位置之间的距离大于 $\sigma/2$，则该智能体会跳跃到一个显著更接近 $C(k)$ 的位置；否则，它会跳跃到距离 $C(k)$ 不超过 $\sigma$ 的位置。因此，如果在时间步 $k$ 时包围圆的半径大于 $\sigma$，则其值将显著减小。

由此可得，系统的所有智能体将在有限的时间步内聚集到半径为 $\sigma$ 的圆盘中，从而证明了定理3（见 [12] 中的定理3）。

4.1.1 聚集到一点

铃木和山下在 [15] 中证明，无法就会合点达成一致的无记忆智能体多智能体系统，无法在有限的时间步内聚集到一点。具备计算其最小包围圆或凸包能力的智能体（该计算的复杂度为 $O(n \log n)$）可以就会合点达成一致，并已被用于在若干先前的研究中证明在有限的时间步内实现向一点聚集，例如见 [1, 2]。铃木和山下在 [15] 中还提出了一种“追逐最远者”算法（该计算的复杂度为 $O(n)$），可实现渐近点收敛。他们的算法是：每个智能体向其最远邻居跳跃一步，步长等于到该邻居距离乘以一个小于1的正常数。因此，在每一步时刻，所有智能体都会跳入其凸包内部，且如果初始构型不是一个点，则此过程将永远不会结束，最终渐近收敛于一点。

我们在此提出一种用于无记忆智能体聚集的替代性简单运动定律，该定律同样需要进行 $O(n)$ 复杂度的计算。由于其简单性，系统将在有限的期望时间步数内完成聚集，而非在有限的时间步数内完成。

为了实现点聚集，我们对运动定律（3）作如下调整。我们将每个智能体的步长限制为到其当前目标的距离，即如果目标的相对位置在 $\sigma$ 的范围内，该智能体将直接移动到目标智能体的位置。因此，我们定义智能体 $i$ 在时刻 $k$ 的步长为：
$$
\mu_i(k) := \min{\sigma, |p_j(k) - p_i(k)|}
$$
其中 $j$ 是目标智能体。

然而，这种限制并不充分，因为一旦所有智能体处于近距离，它们可能在每一步都相互交换位置，而不是聚集到一点。因此，我们还将运动定律（3）的时序调整为半同步模型，使得在每一步中，智能体 $i$ 以一定的概率 $\rho$ 处于激活状态。
$$
p_i(k+1) = p_i(k) + \chi_i(k)\mu_i(k) \frac{p_j(k) - p_i(k)}{|p_j(k) - p_i(k)|} \quad (4)
$$
其中 $j$ 是集合 $N^{\text{Far}}_i(k)$ 中的任意智能体，且 $\chi_i(k)$ 以概率 $\rho$ 或 $1 - \rho$ 分别等于 1 或 0。

接下来，我们证明具有动力学规则（4）的 $n$ 个智能体系统将在有限的期望时间步数内聚集到一点，因为它满足 Gordon 等人所定义的“强异步性假设” [9, 10]。

定义 1 “强异步性假设” ：存在一个严格正的常数 $\varepsilon$，使得对于智能体的任意子集 $A$，在每一时间步 $k$，$A$ 成为唯一活跃智能体集合的概率至少为 $\varepsilon$。

定理 4 具有动力学规则（4）的 $n$ 个智能体系统将在有限的期望时间步数内聚集到一个点。
证明的核心在于，根据运动定律（4），显然，系统凸包的周长不会增加。此外，如果智能体未被限制在直径为 $\sigma$ 的圆盘内，则根据“强异步性假设”，始终存在一个严格为正的概率 $\varepsilon$，使得位于凸包最尖锐角落处的智能体及其附近邻近的智能体成为唯一活跃的智能体，从而跳入凸包内部，导致系统凸包的周长 $l_{CH}(k)$ 产生一个远离零的减少，如下所示：（引理 3 来自 [12]）
$$
l_{CH}(k+1) \leq l_{CH}(k) - \frac{\sigma}{3}\left(1 - \sin\left(\frac{\phi^*}{2}\right)\right)
$$
因此，周长不断减小，直到系统达到所有智能体都被限制在一个 $\sigma$-直径圆盘内的状态。在此状态下，根据运动定律（4），一个活跃智能体会跳跃到另一个智能体的当前位置。因此，在每个时间步，智能体构型所包含的点会持续减少的概率为严格正数 $\varepsilon$，直至在 $\mathbb{R}^2$ 中变为单个点。

因此，点聚集发生的期望时间步长数的上界为
$$
\left(\left\lceil \frac{l_{CH}(0) - 2\sigma}{\frac{\sigma}{3}(1 - \sin(\phi^*/2))} \right\rceil + n - 1\right) \cdot \varepsilon^{-1}
$$
证明定理 4（见 [12] 中的定理4）。

4.2 有限视野

在本节中，我们假设智能体具有有限视野，因此当智能体移动时，系统的可见性图可能会分裂为不连通的组件。“追逐最远者”运动定律（2）在连续时间框架中能够维持可见性图的连通性，但直接进行离散化是行不通的，因为智能体会以较大的步长跳跃，从而可能导致它们与其邻居失去连通性。

我们通过为智能体的步长添加约束来解决此问题，Ando 等人在 [2] 中也提出了这一建议。

设 $\theta_{ij}(k)$ 为从位置 $p_i(k)$ 指向 $p_j(k)$ 的向量与从位置 $p_i(k)$ 指向智能体 $i$ 当前“目标”的向量之间的夹角，并设 $l_{ij}(k)$ 为智能体 $i$ 与智能体 $j$ 当前位置之间的距离。那么，为确保与智能体 $i$ 与智能体 $j$ 之间的可见性，智能体 $i$ 可采取的最大步长由下式给出
$$
\text{Limit} {ij}(k) = \frac{l {ij}(k)}{2 \cos(\theta_{ij}(k)) + \sqrt{(V/2)^2 - (l_{ij}(k)/2)^2 \sin^2(\theta_{ij}(k))}}
$$
且智能体 $i$ 为确保与所有邻居保持可见性的最大步长由以下给出
$$
\text{Limit} i(k) = \min {j \in N_i(k)} {\text{Limit}_{ij}(k)} \quad (5)
$$

此约束的含义是，每一对智能体 ${i,j}$ 不能离开一个直径为 $V$ 且以它们位置的平均值为中心的圆盘。因此，在两个智能体都移动一步后，它们之间的距离不会超过 $V$。如果一个智能体有多个邻居，则它不能离开与其所有邻居相关的圆盘的交集（见图4）。

将限制条件（5）添加到“追逐最远者”运动定律中，得到一种新的运动定律，该定律可保持系统可见性图的连通性。下文将正式提出这一新的运动定律，并证明它能使系统中的智能体聚集到一点。

在提出运动定律之前，我们还需要对智能体 $i$ 的最远邻居集合 $N^{\text{Far}}_i(k)$ 的定义进行如下调整：
设 $l^{\text{Far}}_i(k)$ 为智能体 $i$ 与其最远邻居之间的距离，并令 $\delta < 1/2$ 为一个较小但严格正的常数。那么，智能体 $i$ 的最远邻居集合是其邻居的一个子集，其中从 $i$ 到这些邻居的距离处于 $l^{\text{Far}}_i(k)(1 - \delta)$ 与 $l^{\text{Far}}_i(k)$ 之间，即
$$
j \in N^{\text{Far}}_i(k) \iff l^{\text{Far}}_i(k)(1 - \delta) \leq |p_i(k) - p_j(k)| \leq l^{\text{Far}}_i(k)
$$

然后，假设智能体的行为是在任意时间步 $k$，每个活跃智能体 $i$ 计算 $\psi^{\text{Far}} i(k)$，即包含集合 $N^{\text{Far}}_i(k)$ 中智能体的当前最小角度扇区的角度。如果 $\psi^{\text{Far}}_i(k)$ 大于或等于 $\pi$，则智能体 $i$ 保持不动；否则，它沿方向 $\hat{U}^{\text{Far}}_i(k)$ 跳跃一步长为 $\mu_i(k)$ 的步长，其中 $\hat{U}^{\text{Far}}_i(k)$ 是定义与角度 $\psi^{\text{Far}}_i(k)$ 相关的角平分线的单位向量，而 $\mu_i(k)$ 是以下各量中的最小值：
- $\sigma < V/2$ —— 最大步长
- $\text{Limit}_i(k)$ —— 连通性维护限制
- $l {LRi}(k)$ 是 $\hat{U}^{\text{Far}} i(k)$ 在从 $p_i(k)$ 指向 $p {\text{ExtR}i}(k)$ 和指向 $p_{\text{ExtL}i}(k)$ 的两个向量之和的一半上的投影，其中这两个极值的右、左智能体定义了最小角度扇区。因此，智能体 $i$ 当前的步长不会跨越由这两个极值邻居的位置所定义的线段。

$$
p_i(k+1) = p_i(k) +
\begin{cases}
\chi_i(k)\mu_i(k)\hat{U}^{\text{Far}} i(k), & \psi^{\text{Far}}_i(k) < \pi \
0, & \psi^{\text{Far}}_i(k) \geq \pi
\end{cases}
\quad (6)
$$
其中 $\mu_i(k) = \min{\sigma, \text{Limit}_i(k), l {LRi}(k)}$，且 $\chi_i(k)$ 以概率 $\rho$ 或 $1 - \rho$ 分别等于 1 或 0。

请注意，对于非常小的 $\delta$，除了某些罕见情况外，总是存在一个唯一的最远邻居，此时最小扇区角度为零，因此形成的运动方向是朝向这个唯一的最远邻居的位置。

引理 2 根据动态规则（6），任意一对当前的邻居智能体将永远保持为邻居。
证明 动力学（6）表明，如果一对智能体 ${i,j}$ 在时间步 $k$ 是邻居，则在时间步 $k+1$ 它们的位置被限制在一个直径为 $V$ 的圆盘内，这是由于（5）（步长限制之一）。因此，在任何未来的时间步，任意一对当前邻居之间的距离都不能超过 $V$。

定理 5 具有动态规则（6）且初始构型具有连通的可见性图的 $n$ 个智能体系统，将在有限的期望时间步数内聚集到一点。
在证明中，我们讨论了聚集过程中的两种情况。首先，我们讨论系统中的智能体未被包含在一个直径为 $\sigma$ 的圆盘内的场景。因此，基于一些几何考虑以及智能体构型形成连通的可见性图这一事实，具有特定活动调度的每两个时间步长序列都可能导致系统凸包周长显著减少。根据“强异步性假设”，出现此类序列的概率至少为 $\varepsilon^2$（见 [12] 中的引理7）。

此外，显然根据运动定律（6），系统的凸包周长不会增加，因此智能体将在有限的期望时间步数内聚集到直径为 $\sigma$ 的圆盘中。

其次，我们考虑系统中的智能体包含在一个直径为 $\sigma$ 的圆盘内的情况。因此，任何可能移动的活跃智能体将跳转到其最远邻居的位置，或跳转到其两个最远邻居位置的凸组合处。结果表明，通过连续五个时间步的特定活动调度，系统将聚集到一个点。

设智能体 $i$ 和 $j$ 为在时间步 $k$ 时距离最远的一对智能体，令 $m_{ij}(k)$ 表示位于点 $p_i(k)$ 和 $p_j(k)$ 平均位置的点，并令穿过点 $p_i(k)$ 和 $p_j(k)$ 的直线将平面划分为两个半平面，分别记为 $H_{p1}$ 和 $H_{p2}$。那么，从时间步 $k$ 开始，在每个后续步骤中由活跃智能体集合给出的上述调度如下：
1. 在第 $k$ 个时间步，位于 $H_{p1}$ 的智能体（不包括智能体 $i$ 和 $j$）
2. 在第 $k$ 个时间步 + 1，位于 $H_{p2}$ 的智能体（不包括智能体 $i$ 和 $j$）
3. 在第 $k$ 个时间步 + 2，位于线段 $(p_i(k), m_{ij}(k))$ 上的智能体
4. 在第 $k$ 个时间步 + 3，位于线段 $(m_{ij}(k), p_j(k)]$ 上的智能体
5. 在第 $k$ 个时间步 + 4，位于点 $m_{ij}(k)$ 的智能体

根据“强异步性假设”，出现此类步长序列的概率至少为 $\varepsilon^5$（见 [12] 中的引理 8）。

显然，一旦所有智能体聚集到一个 $\sigma$-直径的圆盘内，它们将一直保持在这个圆盘中，因此智能体将在有限的期望时间步数内聚集到一点，如定理 5 所述（完整证明见 [12] 定理5）。

5 讨论

在这项工作中，我们分析了多智能体系统的多种“追逐最远者”运动定律，以解决相同且无记忆智能体的聚集问题。我们证明了这些简单的运动定律在多种场景下为聚集问题提供了优雅的解决方案。

首先，我们证明了在连续时间框架下，无论具有无限视野还是有限视野，采用“追逐最远者”运动定律的智能体都将在有限时间内聚集到一点。所提出的运动定律及其导致聚集的证明相当简单，但即便如此，仍需仔细处理良定义性和不可微性问题。

在离散时间框架中，情况有所不同，需要更多工作来定义运动规则并获得有意义的收敛结果。我们证明了具有无限视野和固定步长的智能体能够在有限的时间步数内聚集到直径为其步长两倍的圆盘内。为此，我们使用了最小包围圆的半径作为李雅普诺夫函数，分析智能体的位置，并表明它必然会不断减小，直到低于智能体的步长。

此外，我们提出了一种替代的运动定律，以解决在有限的时间步数内实现聚集的问题。该问题的解决方案要求智能体能够就一个会合点达成一致，而这种能力需要较高的计算能力，我们试图避免这一点。我们的替代方案允许系统中的智能体在无需就会合点达成一致的情况下进行聚集，但其结果是智能体只能在有限的期望时间步数内完成聚集。

我们提出了用于 $\mathbb{R}^2$ 平面上多智能体系统的算法和证明，这些方法同样可以轻松地推广到多维空间。