3D数学 学习笔记（2） 矩阵

3D数学 学习笔记（2） 矩阵

参考书籍：
《3D数学基础：图形与游戏开发》

---

矩阵乘法

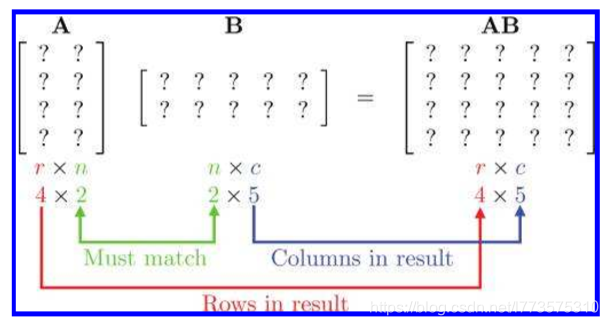
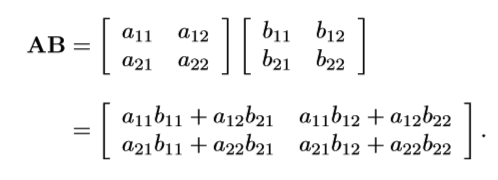
常用等式

** I 为单位矩阵，k为标量，v、w为向量。

• MI = IM = M
• AB ≠ BA
• (AB)C = A(BC)
• (kA)B = k(AB) = A(kB)
• (vA)B = v(AB)
• (AB)^T =B^TA^T （可扩展多个矩阵）
• (v + w)M = vM + wM

注意：用矩阵ABC转换向量v时，用行向量记法为vABC，转换从左往右。用列向量记法为CBAv，转换从右往左。

理解为变换向量

---

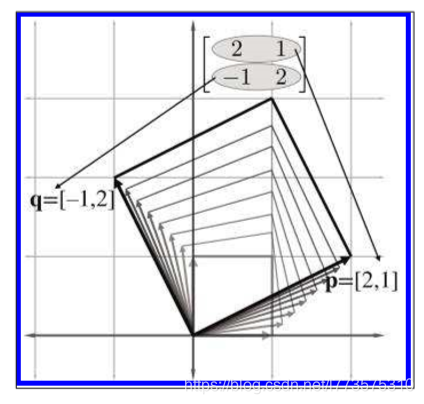
矩阵和线性变换

旋转

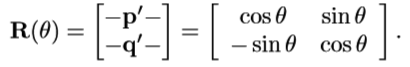
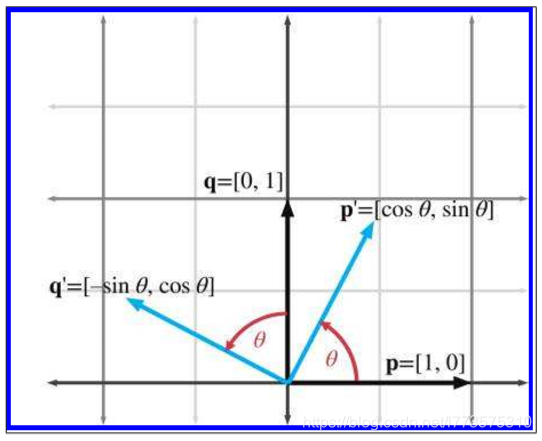
• 绕任意轴（单位向量n）旋转： v′ = v R(n,θ)
  
  

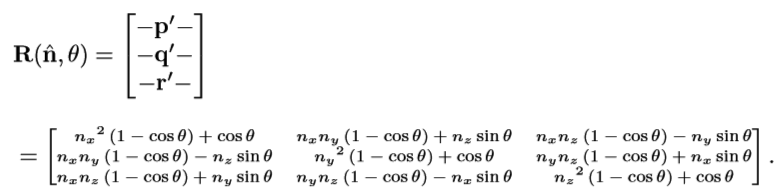
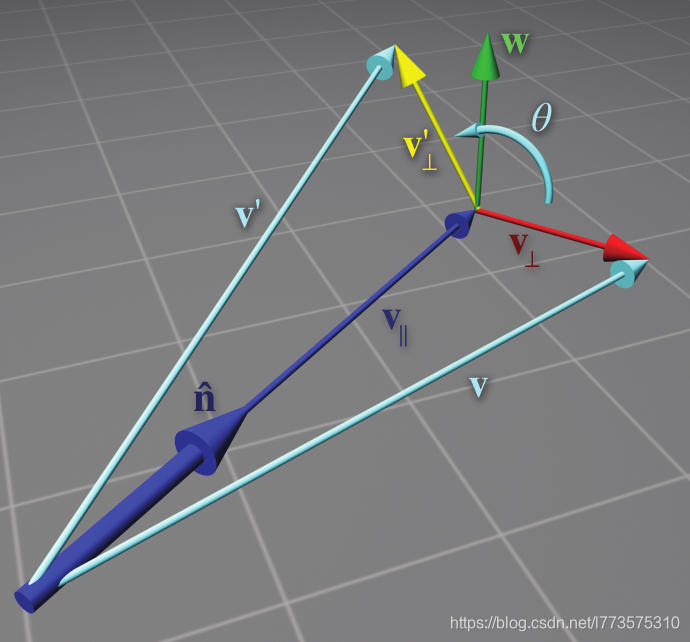
推导思路：

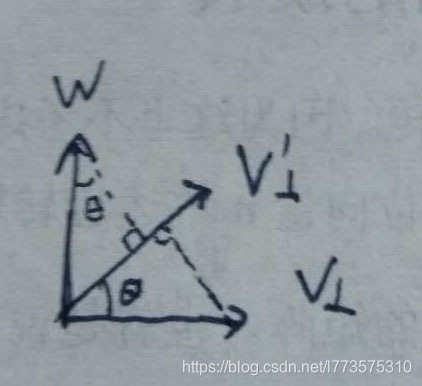
• 计算出旋转后的垂直分量（v′ ⊥）与映射到旋转轴的平行分量（v_||）相加即可。
• v_|| = ( v · n ) n
• v′_⊥ = cosθv_⊥ + sinθw
• w = n × v_⊥

缩放

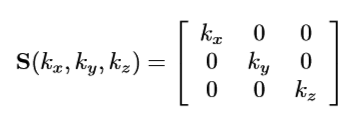
• 绕任意轴（单位向量n）缩放： v′ = v R(n,θ)

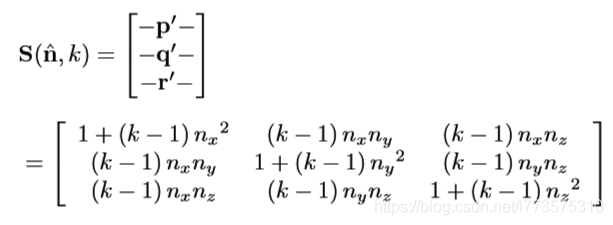
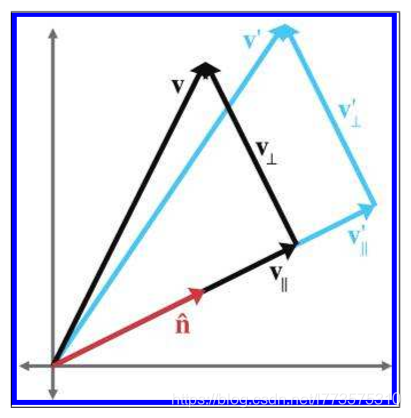
推导思路：

• 通过轴缩放可知道其映射（v′_||）也是相同缩放比例（k），垂直分量不变，所以直接相加即可。
• v′ = v′_|| + v′_⊥
• v′_|| = kv_||
• v′_⊥ = v_⊥

正交投影

投影意味着降维操作（如三维到二维）。正交投影实际是使某个方向用0做缩放因子，将所有点（P）做缩放。

例：P_xy ， 投影到xy平面，即只变换z值，缩放因子为0。

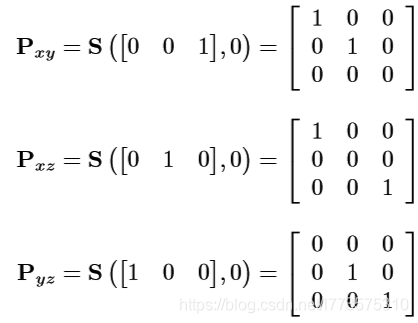
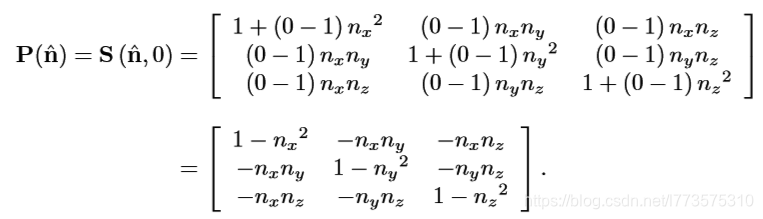
镜像（反射）

即使用缩放因子-1做缩放。

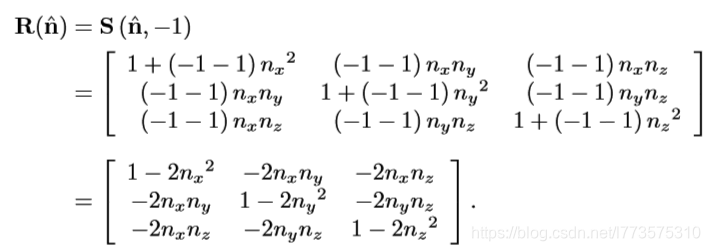
切变（扭曲变换）

例：H_x，x坐标根据坐标y切变。


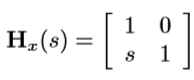
例：H_xy，xy坐标被坐标z改变。

变化的组合

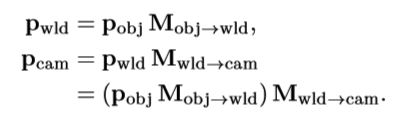
因为矩阵的行向量其实就是变换后的基向量，所以两个矩阵相乘可以简化。

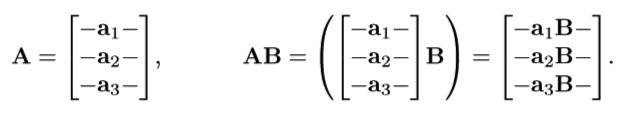
线性变换

如果F保持了基本运算：加法和数量乘，那该映射为线性的。

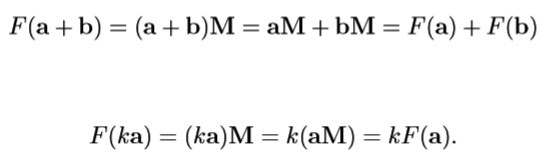
仿射变换

线性变换后接着平移。

• v′ = vM + b

可逆变换

如果存在一个逆变换可以“撤销”原变换，那该变换是可逆的。线性变换中除了投影，其他都可以“撤销”。

• F⁻¹(F(a)) = F(F⁻¹(a)) = a 。

等角变换

两个向量变换前后夹角大小和方向都不变。只有平移、旋转和均匀缩放是等角变换。

正交变换

轴保持互相垂直，而且不进行缩放变换。只有平移、旋转和镜像是正交变换。长度、角度、面积、体积都保持不变。

刚体变换（正规变换）

只有平移和旋转是刚体变换。

变换类型小结

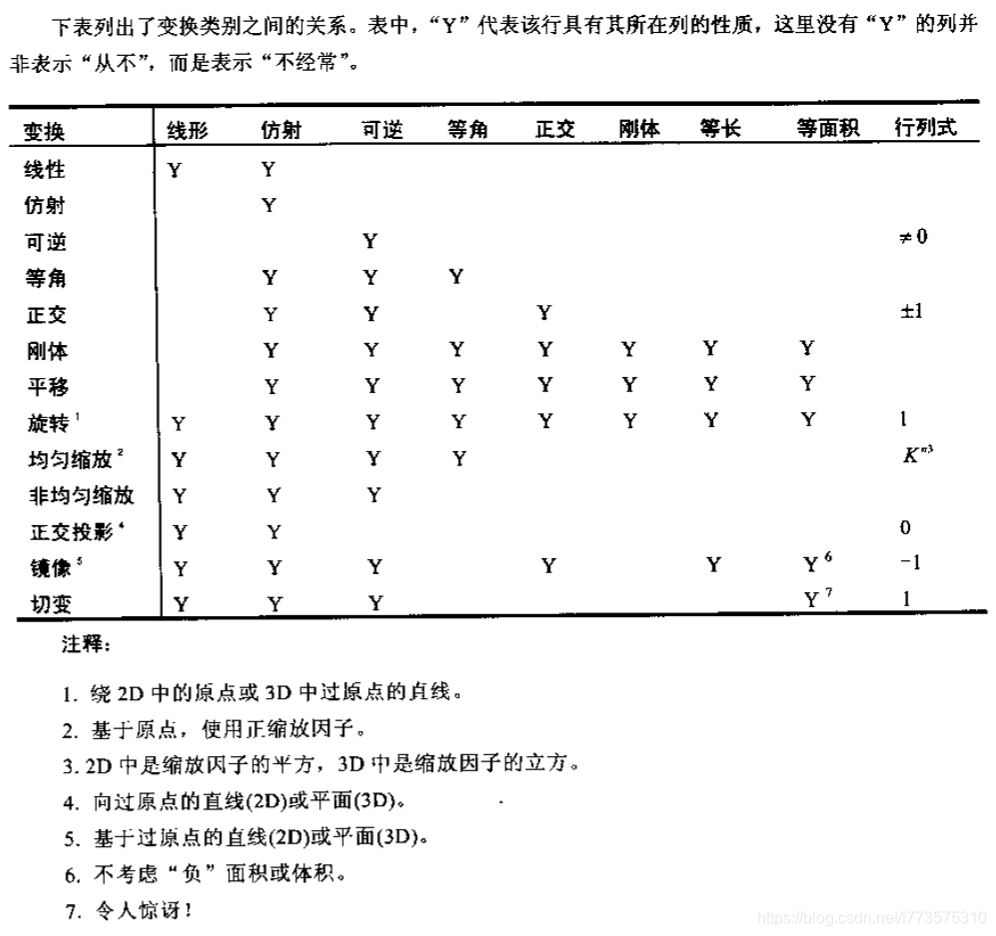
注释7其实没什么好惊讶的。因为切变可以理解为平行四边形内角的变化而已，而其高度和底边长短都没变，所以面积也不会改变。

---

矩阵的行列式

在任意方阵都存在一个标量，称为该方阵的行列式。

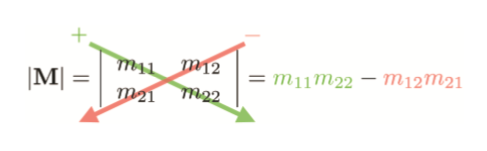
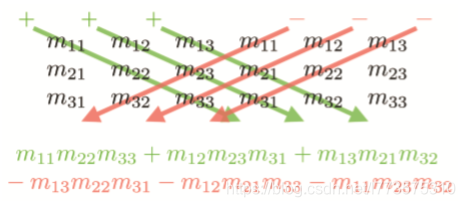
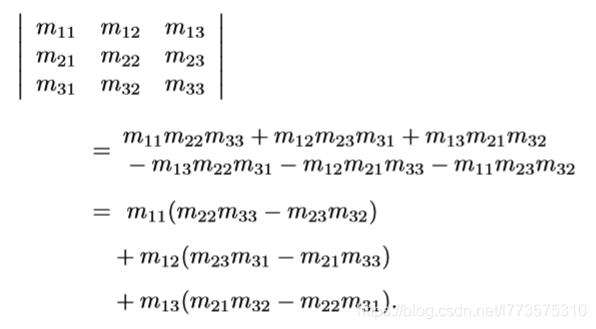
如果方阵三行解释为三个向量，就等价于(a×b)·c。

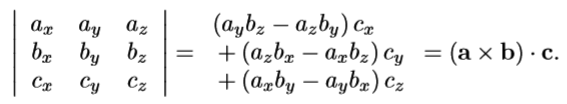
余子式

矩阵M^{{ i j }}表示从M除去第 i 行和第 j 列剩下的矩阵，称作M的余子式。

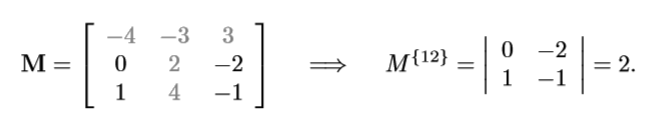
代数余子式

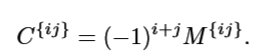
用代数余子式计算方阵的行列式：

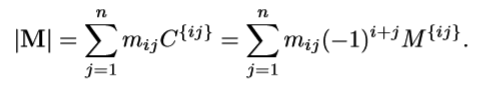
行列式性质

• |AB| =|A||B| （可扩展到多个矩阵）
• |M^T| = |M|
• 矩阵任意行或列为0，行列等于0。
• 交换任意两行或两列，行列式变负。
• 任意行或列加到另一行或列不会改变行列式的值。

几何解释

• 在2D中，行列式等于以基向量为两边的平行四边形的又符号面积。在3D中，变换由里往外翻时行列式变负。
  

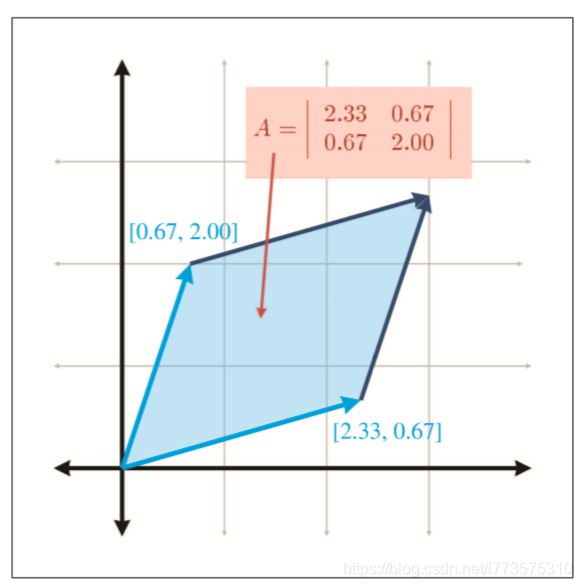
• 如果行列式为0，则该矩阵包含投影。

• 如果行列式为负，则该矩阵包含镜像。

---

矩阵的逆

• M(M^-1) = M^-1M = I （单位矩阵）

方阵，不是所有矩阵都有逆（如某一行全为0），有逆矩阵的矩阵称为可逆或非奇异矩阵，否则为不可逆或奇异矩阵。因为奇异矩阵行列式为0，而非奇异矩阵行列式不为0，所以对任意可逆矩阵M，仅当v=0时，vM = 0。

标准伴随矩阵 （adj M）

定义：为M的代数余子式矩阵的转置矩阵。
计算逆矩阵公式：

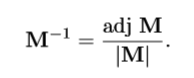
例子：

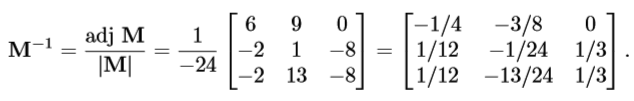
性质

• 非奇异矩阵M，(M^-1)^-1 = M。
• I^-1 = I
• (M^T)^-1 = (M^-1)^T
• (AB)^-1 = A^-1B^-1 可扩展多个矩阵。

几何解释

可以计算“反向”或“相反”变换，模拟“撤销”操作。

---

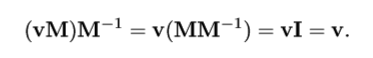
正交矩阵

定义：若方阵是正交的，当且仅当M和其转置M^T的乘积等于单位矩阵。

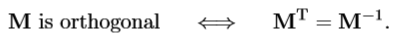
旋转和镜像都是正交的。因为转置矩阵和逆矩阵，所以可以避免计算逆矩阵。

几何解释

正交矩阵满足下列条件：

1. 矩阵的每一行都是单位向量。
2. 矩阵的所有行互相垂直。

• 如果M是正交的，则M^T也是正交的。
• 仅在预先知道矩阵是正交的情况下能利用正交性的优点。否则检测正交性经常是浪费时间的。
• 一组向量互相垂直，称正交基（orthogonal basis）。互相垂直且都是单位向量，称标准正交基向量（orthonoamal basis vectors）。

矩阵正交化

使一些有坏数据或浮点运算累计错误的矩阵正交化，以满足正交性。

施密特正交化：对每一行，减去他平行与已处理部分，最后得到垂直向量，但每次计算只是更正交化，而不是完全正交，所以可以适当的迭代多次得到标准正交基。

---

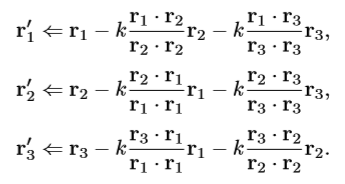
4X4齐次矩阵

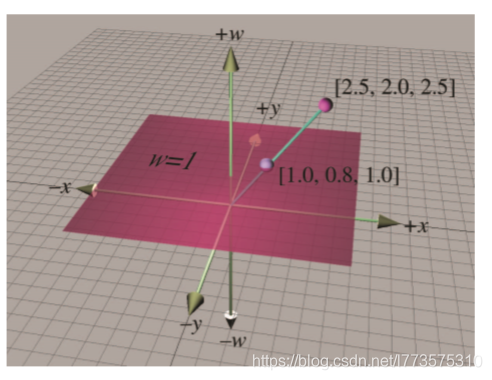
即多一个分量w，称齐次坐标。可以更实现更多变换如平移、仿射、透视等。w为0或1，w=0时，表示无穷远的点。
可以三维向四维的映射。下图是二维xy向三维xyw的映射。

4X4平移矩阵

实际就是4D空间中的切变来实现3D中的平移。

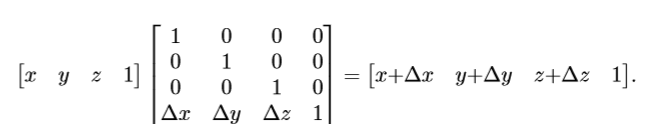
经过向量经过旋转和平移：

如果向量w值为0，则平移不会影响其转换后结果，可以当作“方向”，w为1，可以当做“位置”。下图w为0，可以看到最后结果不受平移影响。

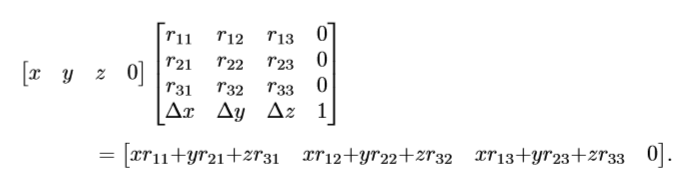
仿射变换

原理是先把变换的“中心点”§平移(T)点到原点，进行线性变换®，再平移(T^-1)回去，即：TRT^-1。

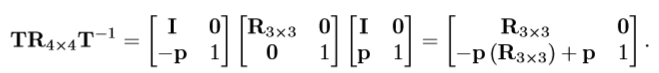
复合变换

约定先进行缩放变换，然后进行旋转，最后平移。

---

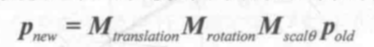
透视投影

w作为投影平面。

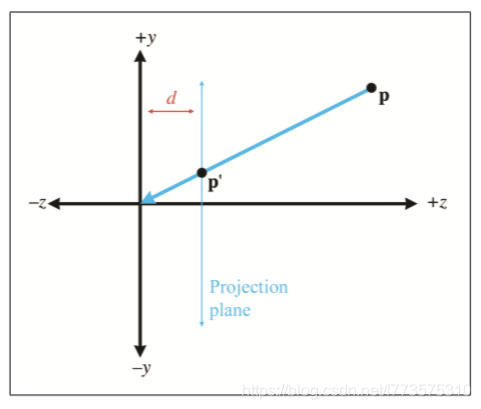
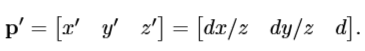
推导到3D空间中：