【动态规划-简单】面试题 08.01. 三步问题

【题目】
三步问题。有个小孩正在上楼梯，楼梯有n阶台阶，小孩一次可以上1阶、2阶或3阶。实现一种方法，计算小孩有多少种上楼梯的方式。结果可能很大，你需要对结果模1000000007。

示例1:

输入：n = 3
输出：4
说明: 有四种走法

示例2:

输入：n = 5
输出：13

提示:

n范围在[1, 1000000]之间

【代码】
【方法1：dp】
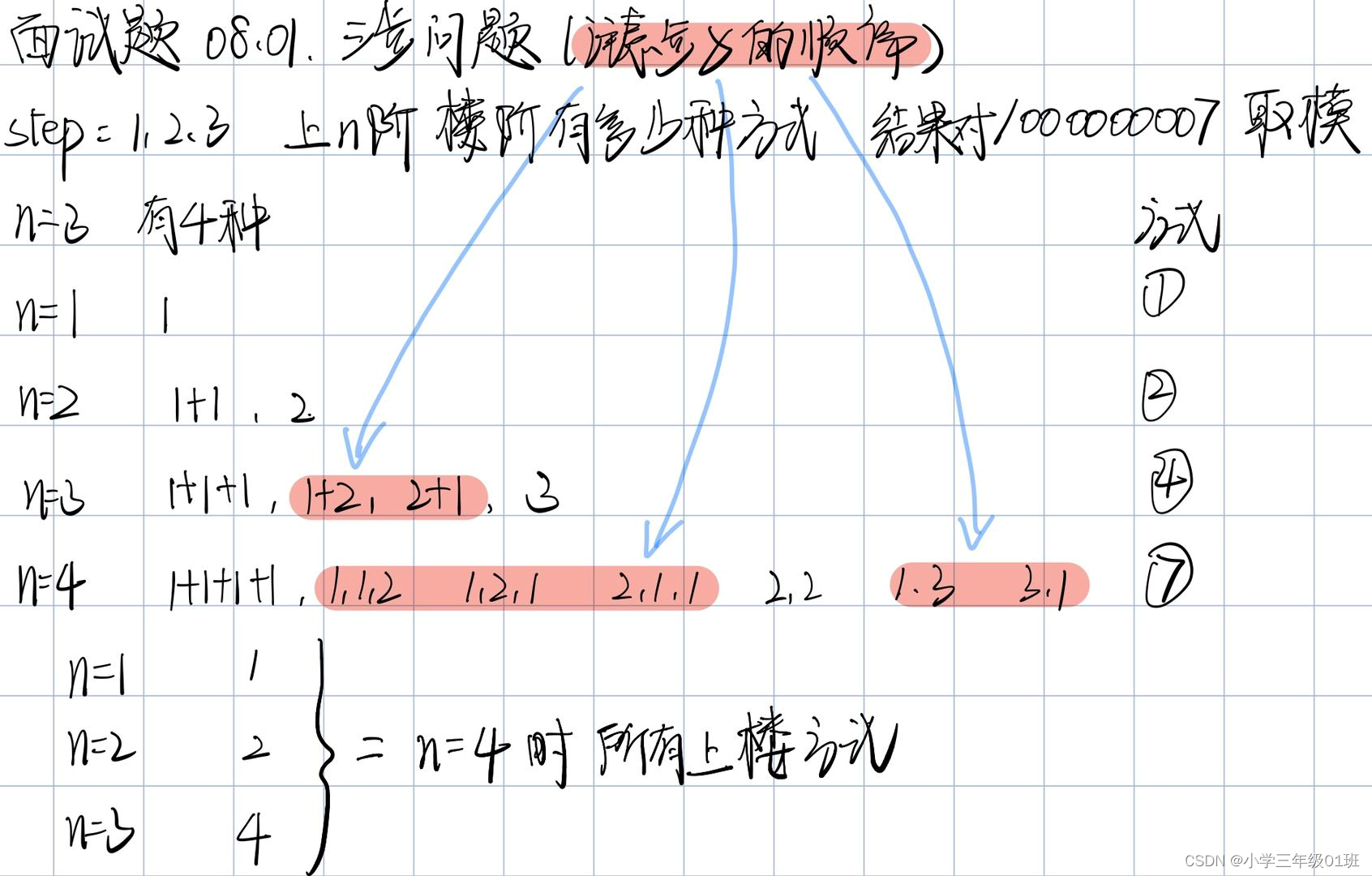cost_n=cost_n-1+cost_n-2+cost_n-3

class Solution:
    def waysToStep(self, n: int) -> int:
        dp=[0,1,2,4]
        for i in range(4,n+1):
            dp.append((dp[i-1]+dp[i-2]+dp[i-3])%1000000007)
        return dp[-1] if n>=4 else dp[n]

【写法2：dp】空间压缩

class Solution:
    def waysToStep(self, n: int) -> int:
        x,y,z=1,2,4
        if n==1:return x
        if n==2:return y
        if n==3:return z
        for i in range(4,n+1):
            x,y,z=y,z,(x+y+z)%1000000007
        return z