低功耗混合ADC设计

低功耗比较器减少型混合ADC设计

摘要

本文提出了一种新型低功耗减少比较器的混合型模数转换器。所提出的ADC采用动态比较器实现高速低功耗转换。为了减小传统动态比较器的失调和反冲噪声效应，本文提出了一种具有高前置放大器增益的低反冲噪声比较器。两个4位模数转换器和8位ADC在 0.18 μm CMOS技术下设计并进行了仿真，电源电压为1.8 V。4位模数转换器的积分非线性(INL)和差分非线性(DNL)分别小于0.4LSB和0.5LSB，而8位ADC的DNL和INL分别为0.83LSB和 1.3LSB。在有效位数(ENOB)分别为3.6位和7.2位的情况下，4位模数转换器在400 Ms∕s采样率下仅消耗1.7 mW，8位ADC在80 MS∕s下消耗4.6 mW。

1. 引言

低分辨率（4–6位）高速（>500Ms/s采样率）模数转换器在基于超宽带(UWB)和无线个人局域网(WPANs)等标准的电池供电系统设计中起着重要作用[1,2]。传统上，由于闪存结构具有低延迟和高数据速率的优势，因此常用于高速低分辨率应用[3]。然而，闪存型ADC在一个时钟周期内完成转换的代价是面积和功耗随分辨率呈指数依赖性增长[2]。折叠和插值技术通过减少比较器数量，可能更适合低功耗操作[2–4]。此外，流水线ADC可以打破这种指数依赖性[5,6]。与闪存型ADC相比，流水线ADC使用较少的比较器，但代价是更高延迟。然而，流水线ADC的线性度受限于余量放大器的有限开环增益，而这些放大器在高速操作时消耗较大的功率[7]。逐次逼近寄存器(SAR)ADC因其仅使用一个比较器即可完成完整转换，成为低功耗应用的合适选择[8,9]。然而，N位SAR ADC需要N个时钟周期才能完成一次转换，限制了其在高速应用中的使用。

最有效的方案（如折叠和插值）主要集中在减少比较器数量上，因为比较器是闪存结构中功耗最高的部分。此外，基于内置偏移电压[10]和反相器[11]的比较器已被引入，以消除电阻梯形网络，后者是闪存型ADC中第二大的功耗来源。然而，通过降低功耗省略电阻梯形网络会带来更多的非线性问题。本文提出了一种比较器减少的混合式ADC，该ADC使用模拟开关来为每个比较器提供适当的参考电压。采用动态比较器代替传统的静态比较器以实现更低的功耗。由于动态比较器在时钟信号的上升沿或下降沿进行判决，因此设计了时序序列以最大化ADC吞吐量。引入了一种对回踢噪声效应敏感度低的高速低失调比较器，以提高ADC线性度。本文其余部分安排如下：第2节描述了提出的ADC结构和比较器的时序序列。第3节解释了比较器的设计。延迟和前置放大器增益的推导也在第3节中给出。参考电压设计在第4节中介绍。第5节讨论了非理想效应。第6节展示了仿真结果，第7节对全文进行总结。

2. 提出的ADC设计

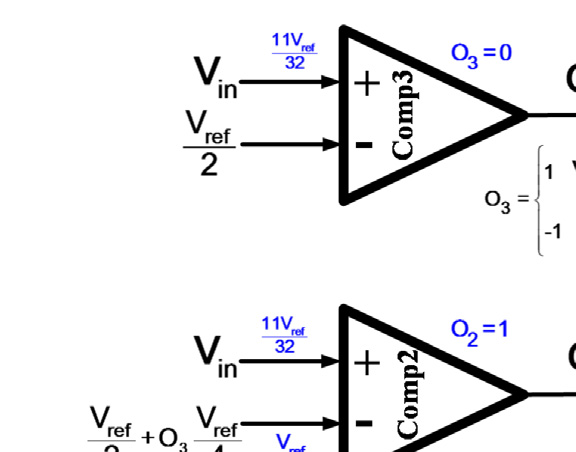
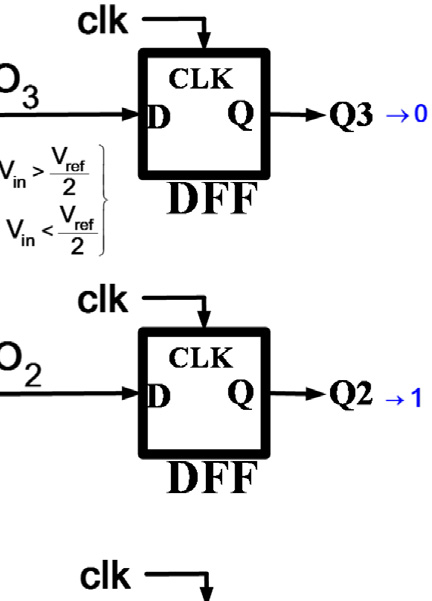
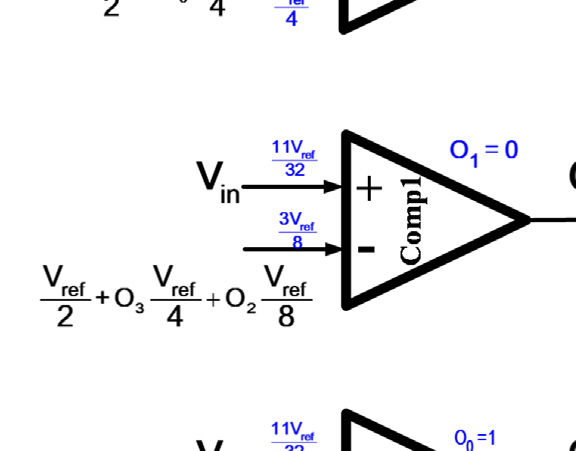
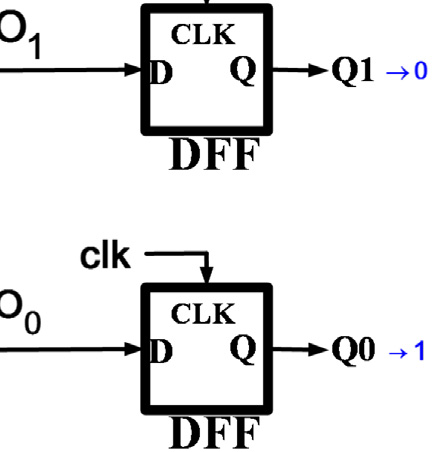
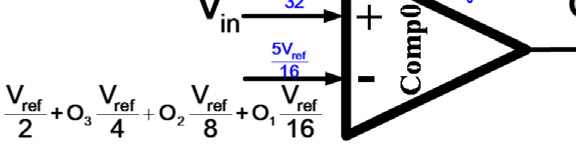
高速闪速型模数转换器需要 $2^N - 1$ 个比较器来实现N位转换。折叠技术通过将模数转换器分为粗调和细调部分，从而减少比较器的数量。折叠操作通常使用放大器实现，尤其在高速和大折叠因子情况下会消耗大量静态功耗。插值技术减少了前置放大器的数量，从而降低了输入电容。然而，锁存器的数量仍与闪存结构相同。通过根据输入电压改变比较器的参考电压，可以减少比较器的数量，如图所示。

图1。在这种结构中，N位转换仅需要N个比较器。如四位模数转换器所示，每个比较器的参考电压根据优先级更高的比较器的输出而变化。为了实现适当的设计，比较器的输出电平被改为−1和1，而不是0和1。例如，如果输入电压为 $11V_{ref}/32$，则comp3的输出将为−1，因为comp3的负输入电压为 $V_{2ref}$。根据comp3的输出，comp2的负输入变为 $V_{2ref} - V_{4ref} = V_{4ref}$。因此，comp2的输出变为1。comp1的负输入变为 $3V_{8ref}$，从而在comp1的输出端产生 −1。同样的过程确定了comp0的输出，如图1所示。

事实上，该技术在速度和功耗之间引入了适当的权衡。与典型的闪存结构相比，该结构的功耗更低。然而，由于比较器输出的顺序行为，其速度较慢。换句话说，该结构的操作方式与逐次逼近型模数转换器（SAR ADC）相同。尽管如此，逐次逼近型模数转换器（SAR ADC）使用一个比较器配合数字部分和N位数模转换器（DAC）来完成转换，而该结构则使用N个比较器实现N位转换，具有更高速度的优势。由于在高速应用中，逐次逼近型模数转换器（SAR ADC）的数字部分消耗大量功耗，因此该结构无需数字部分，其功耗将与逐次逼近型模数转换器（SAR ADC）相当。

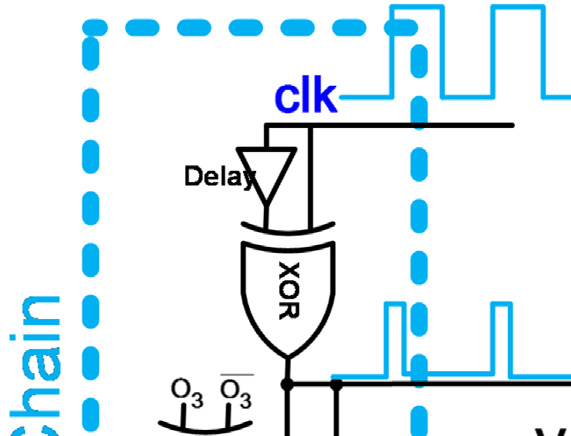
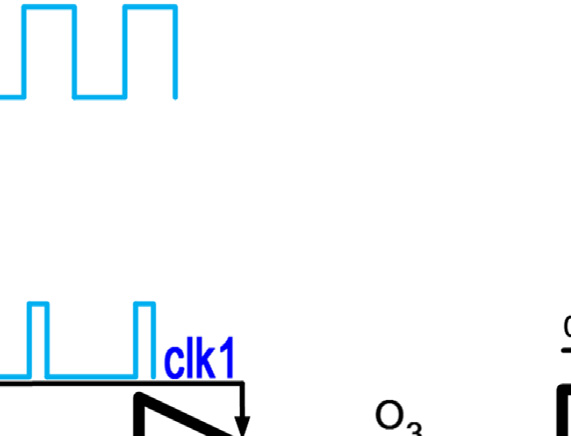
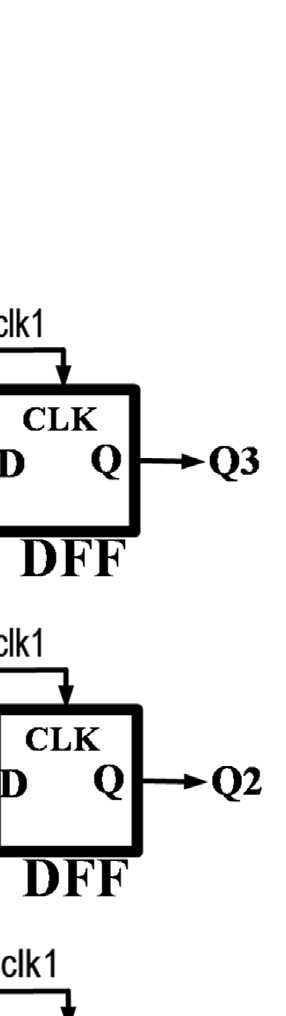
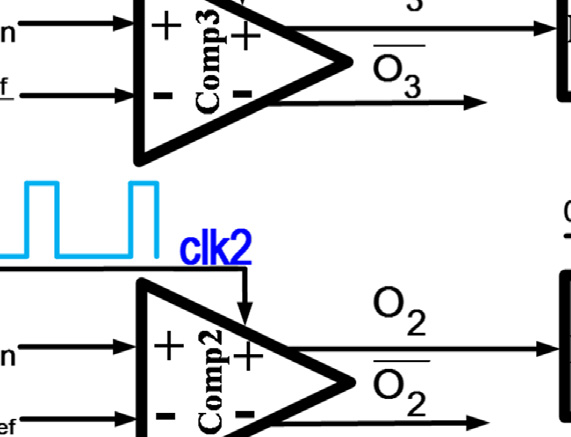
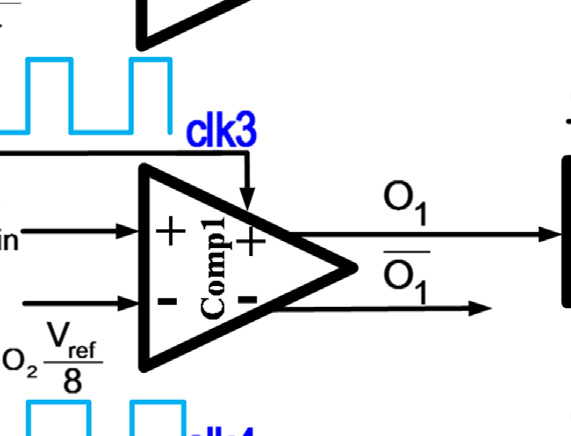
为了完成完整的转换，每个比较器应在输入发生变化时立即更新其输出。因此，这种拓扑结构需要静态比较器才能正常工作。然而，静态比较器消耗大量功耗，这与该拓扑结构降低传统闪存型ADC功耗的初衷相矛盾。提出图2的改进结构是为了利用动态比较器降低图1拓扑的功耗。动态比较器在两个阶段中执行比较；预充电阶段和评估阶段。动态比较器在预充电阶段为比较做准备，然后在评估阶段开始比较。因此，动态比较器的输入应在评估阶段开始前准备好。所以，较低级比较器（例如comp0和comp1）的评估阶段必须在高级比较器（例如comp3和comp2）的评估阶段之后开始。

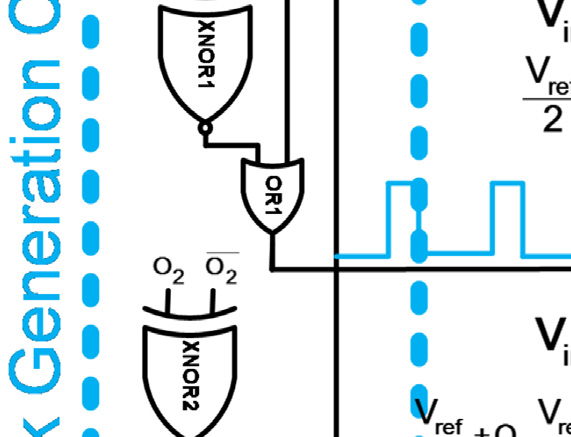
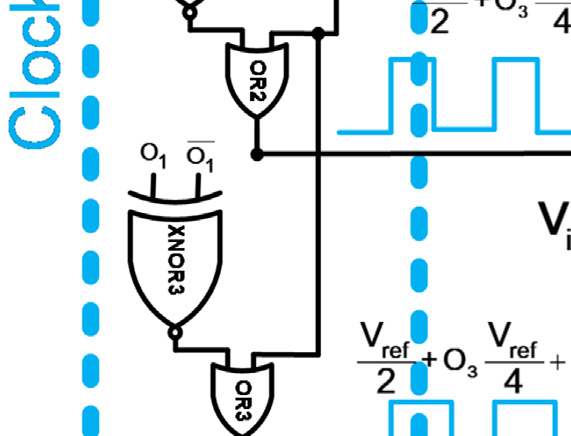
使用时钟生成链来确保每个比较器的评估阶段在其输入准备就绪后才开始。当时钟输入为高电平时，比较器处于预充电阶段；当时钟信号变为低电平时，比较器进入评估阶段。由于预充电阶段所需时间比评估阶段短，因此采用可变脉冲发生器来缩短预充电时间并延长评估时间。一个XNOR门用于判断比较器比较操作的完成情况，然后通过一个OR门确定下一个比较器的评估时间。时钟信号的时序波形如图2b所示。当 clk1为高电平时，comp3处于预充电阶段。comp3在clk1下降到低电平后立即进入评估阶段。此时所有其他比较器仍处于预充电阶段。当 comp3的比较操作完成后，XNOR1的输出变为低电平。因此，OR1的输出下降，comp2的评估阶段开始。该过程依次在comp1和comp0上重复执行。尽管所提出的结构降低了传统闪存型ADC的功耗，但它也降低了模数转换器的转换速率。忽略电压参考源的延迟，N位转换的模数转换器采样率受限于

$$
f_{ADCmax} < \frac{1}{N\tau_{comp}} \tag{1}
$$

其中，$f_{ADCmax}$ 是提出的ADC的最大采样率，$\tau_{comp}$ 是动态比较器的传播延迟。

3. 比较器设计

为了降低功耗并提高传统静态比较器的比较速度，开发了动态比较器[13]。动态比较器采用低失调预放大器来提供可由后续锁存器检测的信号电平。由两个交叉耦合反相器组成的最常见锁存器能够产生强正反馈，以实现快速判决。由于模数转换器速度受限于比较器延迟，高速低功耗比较器是提出的ADC的关键构建模块。

如图3a所示，开发了一种双尾电压比较器，以提高传统单尾动态比较器的速度[14]。当clk信号为高电平时，该比较器处于预充电阶段。如图3b所示，在预充电阶段，前置放大器输出（o+和o−）放电至零，锁存器的两个输出端（out+和out-）充电至Vdd。当时钟clk信号下降时（评估阶段），前置放大器输出立即根据输入信号开始充电。在评估阶段，锁存器根据前置放大器输出进入再生状态。结果，取决于输入信号，锁存器的一个输出端降至低电平，如图3b所示。较高的前置放大器增益可降低锁存器的传播延迟和输入参考失调电压。然而，通过增加前置放大器增益可以减小前置放大器的传播延迟。为了更深入地理解，前置放大器增益和比较器的传播延迟计算如下。

比较器在评估阶段的操作可分为两部分。第一部分是从评估阶段开始到再生锁存器启动点之间的时间段。再生锁存器的启动点可视为其中一个输出节点放电达到PMOS阈值电压的时刻。评估阶段的第二部分是从再生锁存器启动到输出就绪为止。我们将锁存器的第一部分称为放大阶段，第二部分称为判决阶段。在放大阶段，对于微小输入差值，前置放大器的增益可表示为

$$
A_{V_{pre-amplifier}} = \frac{g_{m2}}{C_o t_{amp}} \tag{2}
$$

其中，$g_{m2}$ 是晶体管M2或M3的跨导，$C_o$ 是节点Co−或Co+处的总电容，而$t_{amp}$是放大阶段的时间，即从评估阶段开始到其中一个节点为止的时间。

输出节点以PMOS阈值电压放电。$t_{amp}$ 可通过在输出节点应用基尔霍夫电流定律得到：

$$
\Delta V_{out} = V_{thp} = \frac{1}{C_L} \int_0^{t_{amp}} I_{M10} dt = \frac{1}{C_L} \int_0^{t_{amp}} \beta_{M10}(V_{o-} - V_{thn})^2 dt \tag{3}
$$

其中，$C_L$ 为输出节点处的总电容，$V_{thp}$ 和 $V_{thn}$ 分别为PMOS和NMOS晶体管的阈值电压，$\beta_{10}$ 为M10晶体管的电流因子。对于输入信号的微小差异，M2晶体管的电流为 $I_{M2} = \frac{I_{M1}}{2} + \Delta I_{in} = \frac{I_{M1}}{2} + g_{m2} \Delta V_{in} \approx \frac{I_{M1}}{2}$，近似为常数，且 $V_{o-}$ 可表示为

$$
V_{o-} = \frac{I_{M2}}{C_o} t = \frac{I_{M1}}{2C_o} t \tag{4}
$$

将(4)代入(3)得到：

$$
V_{thp} = \frac{\beta_{M10}}{C_L} \int_0^{t_{amp}} \left(\frac{I_{M1}}{2C_o} t - V_{thn}\right)^2 dt = \frac{2}{3} \frac{\beta_{M10} I_{M1} C_L}{C_o} \left[\left(\frac{I_{M1}}{2C_o} t_{amp} - V_{thn}\right)^3 + V_{thn}^3\right] \tag{5}
$$

求解方程(5)给出

$$
t_{amp} = \frac{2C_o V_{thn}}{I_{M1}} \left[1 + \sqrt[3]{\frac{3}{2} \frac{I_{M1} \beta_{M10} C_L}{C_o} \frac{V_{thp}}{V_{thn}^3} - 1}\right] \tag{6}
$$

因此，通过将(6)代入(2)得到前置放大器增益：

$$
A_{V_{pre-amplifier}} = \frac{2g_{m2} V_{thn}}{I_{M1}} \left[1 + \sqrt[3]{\frac{3}{2} \frac{I_{M1} \beta_{M10} C_L}{C_o} \frac{V_{thp}}{V_{thn}^3} - 1}\right] \tag{7}
$$

方程（7）显示前置放大器增益主要取决于$I_{M1}$，该值由M1、M2和M3的尺寸以及输入信号的共模电压决定。尾电流较大时会降低前置放大器增益，因为 $g_{m2} \propto \sqrt{I_{M1}}$。

比较器的延迟包括在两个放大和判决阶段中的传播延迟。

$$
t_{comp} = t_{amp} + t_{dec} \tag{8}
$$

考虑到锁存器晶体管的输出阈值电压等于 $V_{dd}/2$，锁存器延迟由参考文献[15]给出。

$$
t_{dec} = \frac{C_L}{g_{meff}} \ln\left(\frac{\Delta V_{out}}{\Delta V_0}\right) = \frac{C_L}{g_{meff}} \ln\left(\frac{V_{dd}}{2\Delta V_0}\right) \tag{9}
$$

其中，$g_{meff}$ 是背对背反相器的有效跨导，$\Delta V_0$ 是

$$
\Delta V_0 = |V_{out+}(t = t_{amp}) - V_{out-}(t = t_{amp})| = |V_{thp}| \left(1 - \frac{I_{B11}}{I_{B10}}\right) \tag{10}
$$

其中，$I_{B10}$ 和 $I_{B11}$ 分别是晶体管M10和M11的偏置电流。考虑较小的输入差异时，$\Delta I_{latch} = |I_{B10} - I_{B11}| = g_{m10} \Delta V_{otamp}$ 和 $\Delta V_0$ 可表示为：

$$
\Delta V_0 = |V_{thp}| \left(1 - \frac{I_{B11}}{I_{B10}}\right) = |V_{thp}| \frac{g_{m10} \Delta V_{otamp}}{I_{B10}} \tag{11}
$$

and

$$
\Delta V_{otamp} = \frac{t_{amp}(I_{M2} - I_{M3})}{C_o} = \frac{g_{m2} t_{amp}}{C_o} \Delta V_{in} \tag{12}
$$

将(11)和(12)代入(10)可得

$$
\Delta V_0 = \frac{g_{m10} |V_{thp}|}{I_{B10}} \frac{g_{m2} t_{amp}}{C_o} \Delta V_{in} \tag{13}
$$

因此

$$
t_{dec} = \frac{C_L}{g_{meff}} \ln \left( \frac{I_{B10} g_{m10} |V_{thp}| C_o}{g_{m2} t_{amp} V_{dd} 2 \Delta V_{in}} \right) \tag{14}
$$

因此比较器的延迟是

$$
t_{comp} = t_{amp} + t_{dec} = \frac{2C_o V_{thn}}{I_{M1}} \left[1 + \sqrt[3]{\frac{3}{2} \frac{I_{M1} \beta_{M10} C_L}{C_o} \frac{V_{thp}}{V_{thn}^3} - 1}\right] + \frac{C_L}{g_{meff}} \ln \left( \frac{I_{B10} g_{m10} |V_{thp}| C_o}{g_{m2} t_{amp} V_{dd} 2 \Delta V_{in}} \right) \tag{15}
$$

公式(15)表明，比较器的延迟主要取决于$I_{M1}$的电流。前置放大器的尾电流管和输入晶体管的大尺寸会同时增加$I_{M1}$和$g_{m2}$，从而减小比较器延迟。然而，增大输入晶体管尺寸也会部分增加$C_o$，这限制了比较器延迟的降低。判决阶段的延迟主要取决于两个因素：$C_L$与锁存器晶体管尺寸的比例，以及前置放大器的增益。较大的锁存器晶体管尺寸通过提高$g_{meff}$来减少判决延迟。另一方面，当$C_L$的主要部分由锁存器晶体管的寄生电容引起时，判决延迟仅依赖于前置放大器增益。与$t_{amp}$不同，增大$I_{M1}$会因减小$\Delta V_0$而略微增加$t_{dec}$，因为前置放大器的小信号增益与$1/\sqrt{I_{M1}}$成正比。

前置放大器的输入晶体管（M2和M3）尺寸选择较大，以减小比较器的失调。锁存器晶体管对失调电压的影响被前置放大器的增益所抑制。M1晶体管的尺寸在前置放大器增益和比较器延迟之间引入了权衡。换句话说，M1尺寸较大时会导致延迟较低但前置放大器增益较小，从而引起较大的输入失调电压；减小M1的尺寸可提高前置放大器增益，因此可以获得更小的输入失调电压。对于高速应用，应选择较大的M1尺寸。然而，M1尺寸过大会导致比较器的失调电压增加，从而降低模数转换器分辨率。为了实现高速低失调比较器，提出了图4电路以提高前置放大器增益，在输入晶体管上级联一个交叉耦合对管来提高前置放大器增益。

根据图4b中针对小输入差值建立的模型，计算提出比较器的前置放大器增益。在d−,d+,o−和o+节点列写基尔霍夫电流定律方程，得到结果

$$
g_{ma}(V_{d-} - V_{o+}) = C_o \frac{dV_{o-}}{dt} \tag{16}
$$

$$
g_{mb}(V_{d+} - V_{o-}) = C_o \frac{dV_{o+}}{dt} \tag{17}
$$

$$
-g_{m2}V_{in+} - g_{ma}(V_{d-} - V_{o+}) = C_d \frac{dV_{d-}}{dt} \tag{18}
$$

$$
-g_{m3}V_{in-} - g_{mb}(V_{d+} - V_{o-}) = C_d \frac{dV_{d+}}{dt} \tag{19}
$$

将(17)减去(16)，(19)减去(18)，并考虑$g_{ma} = g_{mb}$和$g_{m2} = g_{m3}$，得到

$$
C_o \frac{d(\Delta V_o)}{dt} - g_{ma} \Delta V_o = g_{ma} \Delta V_d \tag{20}
$$

$$
C_d \frac{d(\Delta V_d)}{dt} + g_{ma} \Delta V_d = g_{m2} \Delta V_{in} - g_{ma} \Delta V_o \tag{21}
$$

代入 $\Delta V_o = V_{o+} - V_{o-}$、$\Delta V_d = V_{d+} - V_{d-}$ 以及 $\Delta V_{in} = V_{in+} - V_{in-}$ 得到结果

$$
\frac{d^2 \Delta V_o}{dt^2} + \frac{g_{ma}(C_o - C_d)}{C_d C_o} \frac{d \Delta V_o}{dt} = \frac{g_{m2} g_{ma}}{C_d C_o} \Delta V_{in} \tag{24}
$$

在输入信号恒定的假设下：

$$
\Delta V_o(t = t_{amp}) \approx \frac{g_{m2} \Delta V_{in}}{C_o - C_d} \left[t_{amp} + \frac{C_o}{C_d} \left(e^{\frac{g_{ma}(C_d - C_o)}{C_d C_o} t_{amp}} - 1\right)\right] \tag{25}
$$

4. 电压参考设计

闪存型ADC中第二大的功耗部分是参考电压发生器。传统的闪存型ADC使用 $2^N$ 个电阻构成的电阻梯形网络来实现N位ADC所需的参考电压。闪存型ADC的线性度取决于参考电压在失配和工艺变化下的偏差，以及比较器的失调。因此，已提出多种校准技术以减小参考电压的偏差 [16]。此外，还引入了内置参考电压比较器，以消除电阻梯形网络，从而节省功耗和面积[10]。然而，其失调值对失配和工艺变化更为敏感。另一种实现参考电压的方法是使用数模转换器（DAC）。与内置失调比较器相比，这种实现方式对工艺变化和失配的敏感性较低，并且相较于电阻梯形网络功耗更低。但其提供参考电压所需时间更长。换句话说，基于DAC的参考电压发生器比内置失调比较器和电阻梯形网络更慢。

由于模数转换器比较器的参考电压需要根据优先级更高的比较器的输出而变化，因此提出的ADC需要一些模拟开关。因此，使用带有模拟开关的内置比较器会带来更大的非线性，因为比较器的阈值会随着模拟开关的状态而改变。图6展示了使用带有模拟开关的电阻梯形网络生成参考电压的两种实现方式，这是一种电阻型DAC。与内置参考电压比较器相比，这些实现方案具有更低的非线性。如图6a所示的模拟开关串联组合不需要任何数字控制电路。然而，它们在提供参考电压时会产生更长的时间延迟，尤其是在更高分辨率的情况下。尽管如图6b所示的并联组合相比串联组合需要驱动更大的电容，但其开关电阻更小。为了降低梯形网络的静态功耗，应选择较大的梯形电阻（R）值。然而，较大的梯形电阻会增加参考电压生成的延迟，并降低模数转换器速度。

为了获得梯形电阻的有效值，使用图7的模型来获取参考电压发生器的延迟。最坏情况下的延迟发生在最低有效位参考电压在 $7V_{ref}/16$ 和 $9V_{ref}/16$ 之间切换时。最坏情况下的Elmore参考电压发生器的延迟可以表示为：

$$
t_{ref_series} = \frac{63R}{16}[9C_{sw} + C_{comp}] + R_{sw}[15C_{sw} + 3C_{comp}] \tag{31}
$$

$$
t_{ref_parallel} = \frac{63R}{16}[9C_{sw} + C_{comp}] + R_{sw}[8C_{sw} + 3C_{comp}] \tag{32}
$$

其中 $C_{sw}$ 为传输门的输入或输出电容，$C_{comp}$ 为每个比较器的输入电容，$R_{sw}$ 为传输门的导通电阻，$R$ 为梯形网络中每个电阻的阻值。公式(31)和(32)表明，并联组合以增加数字控制部分为代价实现了更低的延迟。比较器输入晶体管的尺寸以及因此的 $C_{comp}$ 由模数转换器的失调要求决定。并联组合中开关晶体管的最佳尺寸由公式(32)得出。考虑 $R_{sw} = K_r / (W/L) {sw}$ 以及 $C {sw} = K_c W_{sw} L_{sw}$，其中 $K_r$ 和 $K_c$ 为平衡系数，方程(32)可重写为：

$$
t_{ref} = \frac{63R}{16}[9K_c W_{sw} L_{sw} + C_{comp}] + [8K_r K_c L_{sw}^2 + 3K_r L_{sw} \frac{C_{comp}}{W_{sw}}] \tag{33}
$$

方程(33)表示开关晶体管的长度应选择最小尺寸。通过将方程(32)对 $W_{sw}$ 求导并令其等于零，可得到开关晶体管的最优总宽度：

$$
W_{sw}^{opt} = \sqrt{\frac{16K_r}{189K_c} \frac{C_{comp}}{R}} \tag{34}
$$

因此，开关晶体管的总宽度应根据比较器的输入电容成比例选择。$R$ 的值由模数转换器的速度限制决定。在基于提出的方法的四位模数转换器中，每个比较器的输出应在小于模数转换器采样周期四分之一的时间内准备就绪（$T_s/4$）。由于比较器的决策时间取决于参考电压的准备时间和比较器延迟，因此参考电压生成的时间限制可表示为：

$$
t_{ref} < \frac{1}{4f_s} - t_{comp} \tag{35}
$$

其中 $f_s$ 为模数转换器的采样频率。求解方程(33)–(35)可得 $R$ 的最大值。然而，将 $R$ 从该值减小会导致电阻梯形网络的功耗增加。例如，对于一个四位500 Msps模数转换器，在比较器最坏延迟为400皮秒的情况下，参考电压生成电路的延迟不应超过100皮秒。开关晶体管的最优总宽度约为 $3 \mu m$，$R$ 的最大值约为 $200 \Omega$，在1伏参考电压下静态功耗约为 $300 \mu W$。

5. 非理想效应

5.1. 时钟馈通

与静态比较器相比，动态比较器的判决过程在时钟信号边沿开始。因此，除了反冲噪声外，动态比较器中的时钟馈通也会改变参考电压并限制模数转换器分辨率。参考电压更加由于参考电压采用电阻梯形网络实现且具有较高的输入电阻，因此容易受到时钟馈通的影响。为了实现低功耗，梯形网络的电阻应选择较大的值。然而，大电阻不仅会降低模数转换器速度，还会增加参考电压对反冲噪声和时钟馈通的敏感性。图8显示了当梯形电阻为200 Ω时，时钟馈通对最低有效位比较器参考电压的影响。由于输入信号具有较小的输入阻抗，时钟下降沿会导致输入信号产生微小变化。然而，由于参考电压具有较大的输入阻抗（由电阻梯形网络引起），时钟馈通会使模数转换器分辨率降低约一个最低有效位。图8显示，下降时间为40 ps的时钟信号下降沿可使参考电压从62毫伏变为120毫伏。因此，当比较器在评估阶段开始时启动比较操作时，时钟信号的下降沿改变了参考电压，导致输出错误。实际上，时钟馈通效应引起了一个较大的可变失调，该失调取决于输入信号。

降低时钟馈通效应的第一步是增加时钟信号的转换时间，但这会限制模数转换器速度。由于比较器参考电压处的干扰信号取决于输入晶体管的电容，减小输入晶体管尺寸可降低时钟馈通效应。然而，输入晶体管尺寸过小会增加比较器的失调电压，从而再次限制模数转换器分辨率。减小尾电流可以在降低馈通效应的同时以降低速度为代价。另一种方法是增加输入信号的阻抗导致输入信号和参考电压上产生相同的干扰。然而，比较器的参考电压阻抗彼此不同，并且依赖于输入信号，这需要精确的电压相关阻抗。由于时钟馈通取决于输入信号的阻抗，采用如图9所示的差分结构可以减轻时钟馈通的影响。通常情况下，输入信号的阻抗与参考电压的阻抗不同。因此，在比较器中使用两个差分对以最小化时钟馈通效应，如图9所示。参考电压和输入信号通过差分对实现隔离。尽管由时钟跳变在参考信号和输入信号中产生的干扰电压不同，但这些干扰电压在两个参考输入端或两个信号输入端是相同的。前置放大器的输出电压可表示为：

$$
V_{o+} - V_{o-} = A_p[(V_{in+} - V_{in-}) - (V_{ref+} - V_{ref-})] \tag{36}
$$

其中 $A_p$ 为前置放大器的增益，$(V_{in+} - V_{in-})$ 和 $(V_{ref+} - V_{ref-})$ 分别为差分输入信号和参考电压。由于表达式(36)所示，输入信号和参考电压上的共模干扰被忽略。此外，通过使用图9中的比较器，信号到参考电压的馈通被减小，因为参考电压和输入信号的耦合是通过 $C_{gd}$ 而不是通过 $C_{gs}$，后者是一条阻抗更高的路径。

5.2. 失配

如图6所示，每个比较器的标称触发电平由电阻梯形网络和模拟开关设定。静态偏移和动态偏移对触发电平的改变会降低ADC线性度和信号‐噪声‐失真比(SNDR)。静态偏移的主要来源是比较器中的随机失配和工艺变化，可建模为比较器输入端的失调电压。失调电压的主要来源是前置放大器晶体管的 $\mu C_{ox}$ 失配以及阈值电压 $V_{th}$ 的失配，可建模如下 [16]：

$$
\sigma^2_{V_{th}} \cong \frac{A^2_{V_{th}}}{W \cdot L} \tag{37}
$$

$$
\sigma^2_{\mu} \cong \frac{A^2_{\mu}}{W \cdot L} \tag{38}
$$

其中 $W$ 和 $L$ 分别为晶体管对的宽度和长度，$A^2_{V_{th}}$ 和 $A^2_{\mu}$ 为工艺相关常数。增大晶体管的尺寸如公式(37)和(38)所示，可减小失配效应。总的输入参考比较器失调可以表示为：

$$
V^2_{os} = V^2_{os,23,2‘3’} + \frac{V^2_{os,ab} + V^2_{os,latch}}{A^2_{V_{preamp}}} \tag{39}
$$

其中，$V^2_{os,23,2‘3’}$ 是M2、M3、M2’和M3’晶体管的输入参考失调电压，$V^2_{os,ab}$ 是Ma和Mb晶体管的输入参考失调电压，而 $V^2_{os,latch}$ 是锁存器晶体管总的输入参考失调电压。由锁存器晶体管失配引起的电压失调通过前置放大器的增益得以缓解。如前所述，图4所示电路被提出以提高前置放大器增益，并减小锁存器晶体管的失配效应对电压失调的影响。因此，对于给定的分辨率，可以选择更小尺寸的比较器输入晶体管。这降低了比较器的输入电容，从而根据公式(33)减小了参考电压生成器的延迟。此外，由于比较器的输入电容减小，ADC的功耗也得以降低。

与比较器的静态和动态偏移类似，梯形网络中电阻的失配会改变比较器的触发电平，并降低ADC线性度。电阻失配对差分非线性(DNL)和积分非线性(INL)的影响可以表示为：

$$
DNL = \frac{\Delta R}{R} \cdot LSB \tag{40}
$$

$$
|INL| {max} = \frac{1}{2} \cdot 2^N \cdot \frac{\Delta R}{R} \cdot LSB = \frac{V {REF}}{2} \cdot \frac{\Delta R}{R} \tag{41}
$$

如公式(40)和(41)所示，积分非线性(INL)是决定电阻型DAC分辨率的限制因素，因为其最大值为 $2^{N-1}$ 是DNL的数倍。模数转换器的积分非线性(INL)可以重新改写，同时考虑比较器的失调和电阻的失配，如下所示。

$$
|INL| {max} = \left|\frac{V {REF}}{2} \cdot \frac{\Delta R}{R}\right| + |V_{os}| \tag{42}
$$

为了在参考电压为0.6 V的4位模数转换器中获得小于LSB/4的积分非线性(INL)，电阻之间的失配应小于3.25%，这可以通过对称布局技术和基于 $(\Delta R/R)^2 \cong (\Delta L/L)^2 + (\Delta W/W)^2$（其中 $W$ 和 $L$ 分别为电阻的宽度和长度）表达式的大尺寸电阻轻松实现。增大电阻尺寸会增加寄生电容并降低模数转换器速度。比较器的输入晶体管尺寸选择应使得失调电压小于 $LSB/4 = 9mV$。

提高模数转换器的分辨率需要开关数量的指数增长。事实上，8位、12位和16位模数转换器的主要功耗来源是参考电压源。例如，参考电压生成电路的功耗约占整个4位模数转换器总功耗的20%，占整个8位模数转换器总功耗的55%。此外，参考电压的延迟时间增加会限制模数转换器的速度。例如，对于输入信号为100 mV的情况，8位模数转换器中最低有效位比较器（第8个比较器）的参考电压如图10所示。由于时钟信号所显示的结果，优先级较低的比较器对应的参考电压生成电路延迟更高。在clk与clk1之间的延迟时间小于clk6与clk7之间的延迟时间。这种时间差异是由参考电压生成部分引起的，因为所有比较器本身都是相同的。因此，提高提出的ADC的分辨率会显著限制ADC吞吐量。减少梯形电阻和开关电阻可以在一定程度上补偿这种速度下降，但代价是更高的功耗。此外，高分辨率模数转换器的最低有效位电压降低需要更精密的比较器，这将导致功耗进一步增加。

此外，参考电压对温度变化的灵敏度应小于 $LSB/4$。图11展示了参考电压的实现电路及仿真结果。参考电压对温度的灵敏度为 41 ppm/°C，远小于在 120 °C 温度变化范围内 $LSB/4$ 的值。

6. 仿真结果

为了验证，设计并仿真了两个在TSMC 0.18 μm CMOS技术下的4位和8位比较器减少型模数转换器。4位模数转换器的布局如图12所示，其中有源面积占0.005 mm²。使用1.8 V电源电压和0.6 V参考电压时，4位和8位模数转换器的最低有效位值分别约为37.5 mV和2.3 mV。采用斜率为1 mV/ns的斜坡输入以获得采样率为400 MS/s和80 MS/s时模数转换器的传输曲线。不同编码下4位模数转换器的差分非线性(DNL)和积分非线性(INL)如图13a所示，其中最差情况DNL和INL分别小于0.4最低有效位和0.5最低有效位。图13b显示8位模数转换器的最差情况DNL和INL分别为0.83最低有效位和1.3最低有效位。图14a展示了输入频率为10 MHz和190 MHz时4位模数转换器的模拟输出频谱。输出无杂散动态范围(SFDR)和信噪失真比(SNDR)在10 MHz输入时分别为31.3 dB和23.5 dB，在190 MHz输入时分别为23.9 dB和19.8 dB。8位模数转换器在1 MHz输入时SFDR和SNDR分别为52.5 dB和45.3 dB，在39 MHz输入时分别为47.7 dB和40.1 dB，如图14b所示。

为了分析失配和工艺变化的影响，对330 mV的输入进行了500次蒙特卡洛仿真。图15显示了两种实现方案在蒙特卡洛仿真下的输出码分布。正如预期，由于失配和工艺变化的影响，输出码的标准偏差小于一个最低有效位。在1 MHz输入信号下，不同时钟频率时的有效位数(ENOB)值如图16所示。根据图16，当4位和8位ADC的时钟频率分别超过400 MS/s和80 MS/s时，ENOB性能下降。

提出的ADC通过著名的优值与其它模数转换器在表1中进行比较

$$
FOM = \frac{Power}{2^{ENOB} \times \min(2f_{in}, f_s)} \tag{43}
$$

由于采用了动态比较器，所提出的ADC在相同技术下与其他模数转换器具有相当的功率效率转换性能。因此，该提出的ADC是低功耗中高速应用的合适选择。

和积分非线性 (INL))

随采样率的变化)

表1 模数转换器的性能比较
技术
方案
分辨率（位）
采样率（MS/s）
直流输入下的有效位数（位）
差分非线性（LSB）
积分非线性（LSB）
功耗（毫瓦）
面积 (mm²)
FOM (fJ/转换步)

7. 结论

本文提出了一种新型低功耗减少比较器的混合型模数转换器。该提出的ADC采用动态比较器实现高速、低功耗的转换。为了减小传统动态比较器的失调和反冲噪声效应，本文提出了一种具有更高前置放大器增益的新比较器，并进行了数学分析。通过在 0.18 μm CMOS技术下对两个4位模数转换器和8位ADC进行仿真结果验证了模数转换器性能。4位模数转换器在400 MS/s采样率下，仅从1.8 V电源电压消耗1.7 mW功率，而8位ADC在80 MS/s下消耗4.6 mW。4位模数转换器的差分非线性(DNL)和积分非线性(INL)分别为0.4LSB和0.5LSB。然而，8位ADC的DNL和INL分别为0.83LSB和1.3LSB。