漫谈弹簧阻尼模型（中）

原创已于 2025-06-01 21:06:34 修改 · 1.1k 阅读

CC 4.0 BY-SA版权

文章标签：

于 2025-05-04 22:57:40 首次发布

先谈后者 ${∂u∂x=∂v∂y∂v∂x=−∂u∂y\left\{ \begin{matrix} \frac{\partial u}{\partial x}=\frac{\partial v}{\partial y} \\ \frac{\partial v}{\partial x}=-\frac{\partial u}{\partial y} \\ \end{matrix} \right.$ ，方程冒出个负号，不对称了。传统的教科书把一系列公式不停地折腾，得到这么个式子，让我们去背。实质上该式是具有几何意义的。
若函数 $H(s)H\left( s \right)$ 在开集 $Ω\Omega$ 上是解析的，即存在 $Ω\Omega$ 上的导函数 $H′(s)=k(s)eiθ(s){H}'\left( s \right)=k\left( s \right){{e}^{i\theta \left( s \right)}}$ ，其中 $k(s)k\left( s \right)$ 和 $θ(s)\theta \left( s \right)$ 都是实的，柯西-黎曼方程描述的就是函数和导函数的关系。第一个方程 $∂u∂x=∂v∂y\frac{\partial u}{\partial x}=\frac{\partial v}{\partial y}$ 讲的是 $Ω\Omega$ 上的点 ${s}_{1}$ 处 $x$ 方向的导数和 $y$ 方向的导数相等，实际上该点任意方向的导数都相等。光有这个条件不够，因为复平面的翻转也具有该性质，而翻转不是解析的，第二个公式 $∂v∂x=−∂u∂y\frac{\partial v}{\partial x}=-\frac{\partial u}{\partial y}$ 加上补充，在常规的x-y和u-v平面上，左侧 $∂v∂x\frac{\partial v}{\partial x}$ 表示的是x方向的变化 $△x\vartriangle x$ 对它旋转90°的v方向的 $△v\vartriangle v$ 的影响，右侧 $−∂u∂y-\frac{\partial u}{\partial y}$ 表示y方向的变化 $△y\vartriangle y$ 和它旋转90°的-u方向的 $−△u-\vartriangle u$ d的影响，这种影响作用是相等的，由下图可知，这种“作用”的值是 $ksin⁡θk\sin \theta$ 。
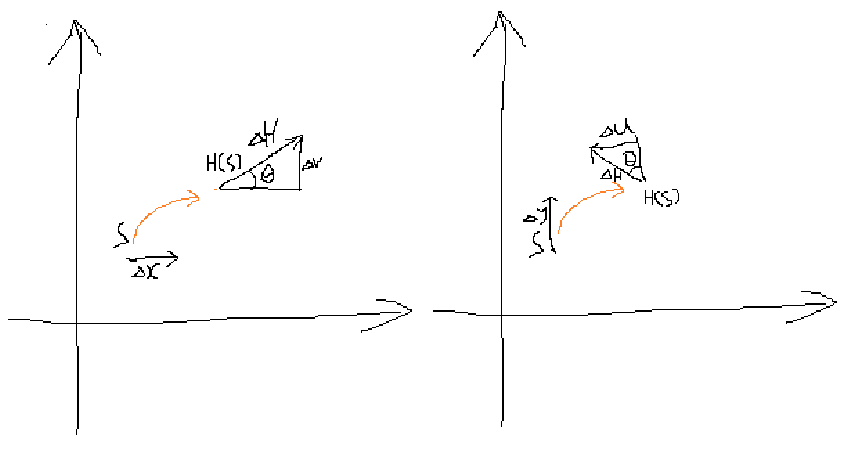
在这里插入图片描述
再谈前者，沿着平面上闭合曲线 $γ\gamma$ 对平面上二维解析函数形成的向量场 $F→=Pi→+Qj→\overrightarrow{F}=P\overrightarrow{i}+Q\overrightarrow{j}$ 积分，有 $∮γF→dl→=∮γPdx+Qdy=∬D(∂Q∂x−∂P∂y)dxdy\oint_{\gamma}{\overrightarrow{F}d\overrightarrow{l}=}\oint_{\gamma}{Pdx+Qdy=\iint_{D}{\left( \frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y} \right)}}dxdy$ ，
其中 $D$ 指 $γ\gamma$ 围成的区域。
将 $P$ 换成 $u$ 、 $Q$ 换成 $- v$ 可求环量 $∮γ(udx−vdy)=∬D(−∂v∂x−∂u∂y)dxdy\oint_{\gamma }{\left( udx-vdy \right)=\iint_{D}{\left( -\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y} \right)}}dxdy$
将 $P$ 换成 $v$ 、 $Q$ 换成 $u$ 可求通量 $∮γvdx+udy=∬D(∂u∂x−∂v∂y)dxdy\oint_{\gamma}{vdx+udy=\iint_{D}{\left( \frac{\partial u}{\partial x}-\frac{\partial v}{\partial y} \right)}}dxdy$
将柯西-黎曼方程带入，结果都是0。

5.3 弹簧阻尼模型的向量场

在复分析的学习中， $1s\frac{1}{\text{s}}$ 和 $−1s-\frac{1}{\text{s}}$ 是一对，一个是源一个是汇，两者相加为0，是场的作用的叠加性质的体现。
在线性系统中， $1s\frac{1}{\text{s}}$ 和 $s$ 是一对，两者乘积为1，是一种串联的接续作用。所有传递函数的波利亚向量场图像都是图(5.2)和图(5.6)的平移之后，在各点处相乘而来，这就是传递函数的几何直观（复函数的几何直观方法挺多的，尼达姆的《复分析：可视化方法》对此做了很多精彩的工作）。
读者会看到弹簧阻尼模型是力学模型，而本章讨论零极点用的是电学模型，它们之间存在某种对应关系吗？我的回答是，不知道。我看过很多不同领域之间的类比，依据的是数学抽象上形式的一致性，确实能给人很多启发。案头上摆着两本著作：杜功焕《声学基础》、张海澜《理论声学》，都有专门的章节介绍。但在我看来，这种类比并不意味着双方死绑在一块，只是数学形式一致而已。
将传递函数 $H\text{H}$ 分解成 $H1{{\text{H}}_{\text{1}}}$ 和 $H2{{\text{H}}_{\text{2}}}$ ，存在 $H=H1H2=H2H1\text{H=}{{\text{H}}_{1}}{{\text{H}}_{2}}\text{=}{{\text{H}}_{2}}{{\text{H}}_{1}}$ ，满足乘法交换律，这又提示我们线性系统是在二维空间上做的游戏，因为在更高维的空间， $H1H2{{\text{H}}_{1}}{{\text{H}}_{2}}$ 一般不等于 $H2H1{{\text{H}}_{2}}{{\text{H}}_{1}}$
有意思的是， $H(s)H\left( s \right)$ 也可以分解成成 $H1{{\text{H}}_{\text{1}}}$ $+$ $H2{{\text{H}}_{\text{2}}}$ ，比如式(2.1)就可以分解成 $H(S)=1m(1s1−s2(s−s1)+−1s1−s2(s−s2))H\left( S \right)=\frac{1}{m}\left( \frac{\frac{1}{{{s}_{1}}-{{s}_{2}}}}{\left( s-{{s}_{1}} \right)}+\frac{-\frac{1}{{{s}_{1}}-{{s}_{2}}}}{\left( s-{{s}_{2}} \right)} \right)$ 。两种形式的向量场是一致的。
让我们看看式(2.1)表示的向量场图像。通过调整 $α\alpha$ 的值，我们可以得到3种场，分别是对应过阻尼、临界阻尼、欠阻尼。
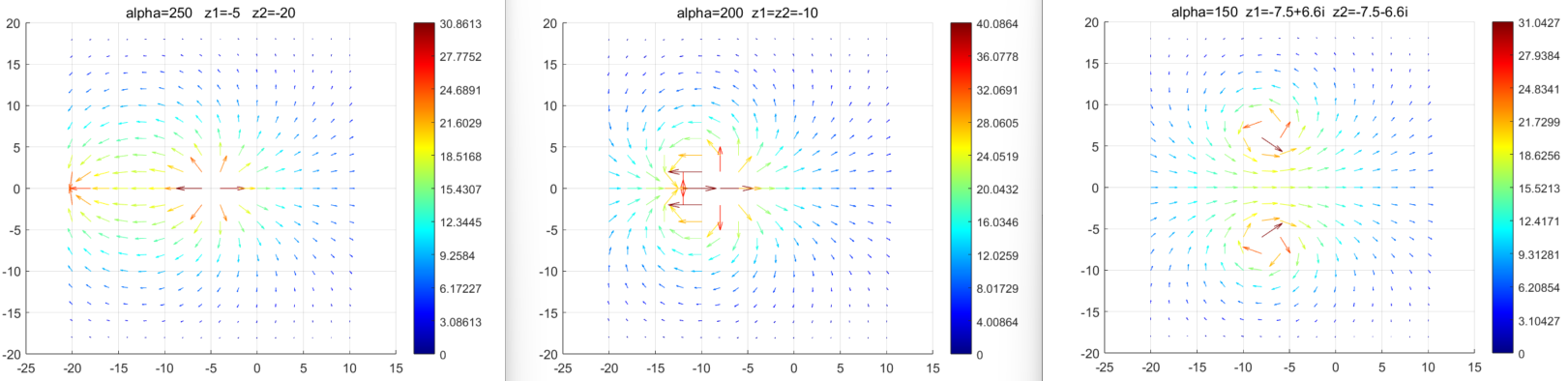
在这里插入图片描述
NVH的同事会知道在临界阻尼的情况下，弹簧振子会以最快的速度恢复到平衡状态，时域图能看得很清楚。在这三张图，我们能得到新的解释：临界阻尼，极点远虚轴最远；欠阻尼， $α\alpha$ 变小，极点靠近虚轴同时远离实轴；过阻尼，极点靠近虚轴。由图(1.3)和式(2.8)、(2.9)也能看出来。

六再谈谈二阶微分方程

我们取式(1.2)的齐次部分，引入微分算子“ $D=ddt\text{D}=\frac{d}{dt}$ ”，公式可以改写成
$D2x+a1Dx+a2x=0(6.2){{\text{D}}^{2}}x+{{a}_{1}}\text{D}x+{{a}_{2}}x=0\tag{6.2}$
再定义“ $P(D)={{D}^{2}}+{{a}_{1}}D+{{a}_{2}}$ ”，公式可以进一步改写成
$P(D)x=0(6.2)P(D)x=0\tag{6.2}$
这种形式是表示 $x$ 被映射到0，提示了我们一种解齐次方程的新思路（工科生将这部分问题称作零输入响应）。从线性映射的角度，可将式(6.2)的求解看成寻找 $P (D)$ 的零空间的问题。
接着， $P (D)$ 还可以做因式分解
$P(D)=(D+n1)(D+n2)P(D)=\left( D+{{n}_{1}} \right)\left( D+{{n}_{2}} \right)$
表示二阶系统可以看成是两个一阶系统级联依次作用于 $x$ 。这种看法有助于我们理解一阶微分方程组。在我看来所有的高阶微分方程都可以在某种形式上看成是一阶的，比如 ${{D}^{m}}x(m>1)$ ，完全可以写成 $D{{D}^{m-1}}x=Dy$ 。从这个想法出发，我把一阶微分看成是速度，二阶微分就是速度的速度，以此类推，不管是在实数、复数还是在其他域，这种看法有助于建立物理图景。对于工程师而言，一阶方程的数值计算是很简单的，那么高阶方程的数值解就可以用一阶方程组的数值解来替代，超简单的啦。
式(1.2)用一阶微分方程组来改写，就是
$[d2dt2xddtx]=[a1a210][ddtxx]+[F~(t)0]\left[ \begin{matrix} \frac{{{d}^{2}}}{d{{t}^{2}}}x \\ \frac{d}{dt}x \\ \end{matrix} \right]=\left[ \begin{matrix} {{a}_{1}} & {{a}_{2}} \\ 1 & 0 \\ \end{matrix} \right]\left[ \begin{matrix} \frac{d}{dt}x \\ x \\ \end{matrix} \right]+\left[ \begin{matrix} \tilde{F}(t) \\ 0 \\ \end{matrix} \right]$
$ddt[x1x2]=[a1a210][x1x2]+[F~(t)0](6.3)\frac{d}{dt}\left[ \begin{matrix} {{x}_{1}} \\ {{x}_{2}} \\ \end{matrix} \right]=\left[ \begin{matrix} {{a}_{1}} & {{a}_{2}} \\ 1 & 0 \\ \end{matrix} \right]\left[ \begin{matrix} {{x}_{1}} \\ {{x}_{2}} \\ \end{matrix} \right]+\left[ \begin{matrix} \tilde{F}(t) \\ 0 \\ \end{matrix} \right]\tag{6.3}$
式(6.2)再加上 $y={{x}_{2}}$ ，便构成了现代控制理论所说的状态方程，这个式子具有很强的工程意义。
由此，便可以对图1.1重新绘制，画出由更简单的一阶系统组成的等效模型。
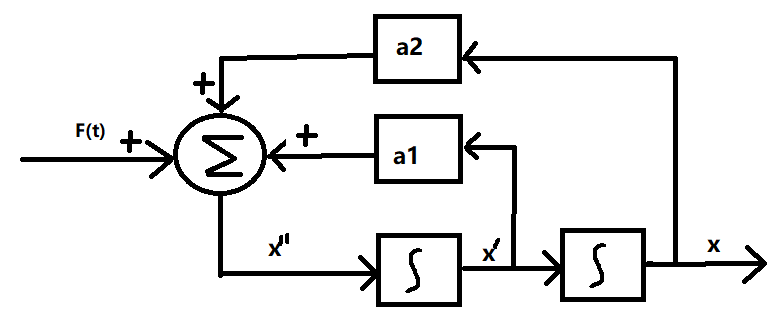
在这里插入图片描述
工程上，得到该模型的下一步就是求出它的齐次解。求解，实际上就是在研究矩阵 $[a1a210]\left[ \begin{matrix} {{a}_{1}} & {{a}_{2}} \\ 1 & 0 \\ \end{matrix} \right]$ ，具体的说就是讨论它特征值的三种情况：不同的实特征值、重复的实特征值，共轭的复特征值。读者将会发现，这分别对应着过阻尼、临界阻尼、欠阻尼。

七写在最后

世界上人分两种，一种是聪明人，一种是蠢人，蠢人就是用来给聪明人骗的，而我属于蠢的那种。上海有很多聪明人，而我在那里混了两年多。方方，还有袁sir，常对我说，要对自己好一点。多少次路过阿拉的咖啡店，扫个码，摸摸口袋里的钱，然后给他俩发消息，真的想对自己好一点。有次坐在电脑前，李队长路过，“哦，你会电脑啊，帮我打字呗”，看着队长发过来的聪明人的诈骗案例，几百万级别，就像在梦里边一样。在一个特殊的时间节点，方方给我发来一张图，委屈巴巴的，上面写着“没有钱”，仿佛看到了方方的泪水，打湿了猪脚饭。小高，混的不好，老高，被裁了。有次去上海，离开了才和老高打招呼，跟他讲，混的不好，不想联系。还认识一个姓高的，山东省科学院的高老师，老师活跃得很，同院的史老师，也是一位热心人，给我出过一道题，三反应池传质浓度计算，刚好是解微分方程的，挺经典的初值问题，我附到本文末尾。在那个困难时刻，有道题做做，就当散散心了。

7.1 解法一：一阶常微分的解法

7.1.1 反应池1

反应池1液体浓度变化分为两个阶段，阶段一注入的是葡萄糖溶液瓶，浓度是 ${{C}_{01}}$ ，阶段二注入的是蒸馏水，浓度是 $0 g / m L$ 。

7.1.1.1 阶段1

考虑一个很短的时间 $Δt\Delta t$ 内，
输出液体体积是 $Δt⋅vf\Delta t\cdot {{v}_{f}}$ ，液体的浓度是 ${{C}_{1}}(t)$ ，得输出的葡萄糖质量是 $C1(t)⋅Δt⋅vf{{C}_{1}}(t)\cdot \Delta t\cdot {{v}_{f}}$ 。
输入液体体积是 $Δt⋅vf\Delta t\cdot {{v}_{f}}$ ，液体的浓度是 ${{C}_{01}}$ ，得输入的葡萄糖质量是 $C01⋅Δt⋅vf{{C}_{01}}\cdot \Delta t\cdot {{v}_{f}}$ 。
液体的浓度 $C1(t+Δt)=C1(t)⋅V−C1(t)⋅Δt⋅vf+C01⋅Δt⋅vfV{{C}_{1}}(t+\Delta t)=\frac{{{C}_{1}}(t)\cdot V-{{C}_{1}}(t)\cdot \Delta t\cdot {{v}_{f}}+{{C}_{01}}\cdot \Delta t\cdot {{v}_{f}}}{V}$
$C1(t+Δt)−C1(t)=−C1(t)⋅Δt⋅vf+C01⋅Δt⋅vfV{{C}_{1}}(t+\Delta t)-{{C}_{1}}(t)=\frac{-{{C}_{1}}(t)\cdot \Delta t\cdot {{v}_{f}}+{{C}_{01}}\cdot \Delta t\cdot {{v}_{f}}}{V}$
$C1(t+Δt)−C1(t)Δt=−C1(t)⋅vf+C01⋅vfV\frac{{{C}_{1}}(t+\Delta t)-{{C}_{1}}(t)}{\Delta t}=\frac{-{{C}_{1}}(t)\cdot {{v}_{f}}+{{C}_{01}}\cdot {{v}_{f}}}{V}$
当 $Δt→0\Delta t\to 0$ ，可得浓度变化的速度 $C1(t+Δt)−C1(t)Δt=−vfVC1+C01⋅vfV\frac{d{{C}_{1}}}{dt}=\underset{\Delta t\to 0}{\mathop{\lim }}\,\frac{{{C}_{1}}(t+\Delta t)-{{C}_{1}}(t)}{\Delta t}=-\frac{{{v}_{f}}}{V}{{C}_{1}}+\frac{{{C}_{01}}\cdot {{v}_{f}}}{V}$
可得通解 $C1(t)=C01+αe−vfVt(1.1){{C}_{1}}\left( t \right)={{C}_{01}}+\alpha {{e}^{-\frac{{{v}_{f}}}{V}t}}\tag{1.1}$
将初值 $C1(0)=0{{C}_{1}}\left( 0 \right)=0$ 带入式（1.1）可得
$C1(t)=C01−C01e−vfVt(1.2){{C}_{1}}\left( t \right)={{C}_{01}}-{{C}_{01}}{{e}^{-\frac{{{v}_{f}}}{V}t}}\tag{1.2}$
阶段一持续的时间是 $T=0.05vf(s)T=\frac{0.05}{{{v}_{f}}}(s)$

7.1.1.2 阶段2

令 $t^=t−T\hat{t}=t-T$ ，即阶段二从 $t^=0\hat{t}=0$ 开始，浓度 $C^1(t^)=C1(t^+T){{\hat{C}}_{1}}\left( {\hat{t}} \right)={{C}_{1}}\left( \hat{t}+T \right)$
初值是 $C^1(0)=C1(T)=C01−C01e−vfVT{{\hat{C}}_{1}}\left( 0 \right)={{C}_{1}}\left( T \right)={{C}_{01}}-{{C}_{01}}{{e}^{-\frac{{{v}_{f}}}{V}T}}$
$C^1(t^+Δt^)=C^1(t^)⋅V−C^1(t^)⋅Δt^⋅vfV{{\hat{C}}_{1}}\left( \hat{t}+\Delta \hat{t} \right)=\frac{{{{\hat{C}}}_{1}}\left( {\hat{t}} \right)\cdot V-{{{\hat{C}}}_{1}}\left( {\hat{t}} \right)\cdot \Delta \hat{t}\cdot {{v}_{f}}}{V}$
$C^1(t^+Δt^)−C^1(t^)Δt=−vfVC^1(t^)\frac{{{{\hat{C}}}_{1}}\left( \hat{t}+\Delta \hat{t} \right)-{{{\hat{C}}}_{1}}\left( {\hat{t}} \right)}{\Delta t}=-\frac{{{v}_{f}}}{V}{{\hat{C}}_{1}}\left( {\hat{t}} \right)$
$dC^1dt^=−vfVC^1\frac{d{{{\hat{C}}}_{1}}}{d\hat{t}}=-\frac{{{v}_{f}}}{V}{{\hat{C}}_{1}}$
$C^1(t^)=ce−vfVt^(1.3){{\hat{C}}_{1}}\left( {\hat{t}} \right)=c{{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}}\tag{1.3}$
将初值代入式（1.3）得
$C^1(t^)=C1(T)⋅e−vfVt^(1.4){{\hat{C}}_{1}}\left( {\hat{t}} \right)={{C}_{1}}\left( T \right)\cdot {{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}}\tag{1.4}$

7.1.1.3 结果

由式（1.2）和式（1.4）可得
${C1(t)=C01−C01e−vfVtt≤T=0.05vfC^1(t^)=C1(T)⋅e−vfVt^t>T\left\{ \begin{matrix} {{C}_{1}}\left( t \right)={{C}_{01}}-{{C}_{01}}{{e}^{-\frac{{{v}_{f}}}{V}t}} & t\le T=\frac{0.05}{{{v}_{f}}} \\ {{{\hat{C}}}_{1}}\left( {\hat{t}} \right)={{C}_{1}}\left( T \right)\cdot {{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}} & t>T \\ \end{matrix} \right.$
即
${C1(t)=C01−C01e−vfVtt≤T=0.05vfC1(t)=C1(T)⋅e−vfV(t−T)t>T\left\{ \begin{matrix} {{C}_{1}}\left( t \right)={{C}_{01}}-{{C}_{01}}{{e}^{-\frac{{{v}_{f}}}{V}t}} & t\le T=\frac{0.05}{{{v}_{f}}} \\ {{C}_{1}}\left( t \right)={{C}_{1}}\left( T \right)\cdot {{e}^{-\frac{{{v}_{f}}}{V}\left( t-T \right)}} & t>T \\ \end{matrix} \right.$

7.1.2 反应池2

反应池2液体浓度变化也分为两个阶段，和反应池1一一对应。

7.1.2.1 阶段1

考虑一个很短的时间 $Δt\Delta t$ 内，
输出液体体积是 $Δt⋅vf\Delta t\cdot {{v}_{f}}$ ，液体的浓度是 ${{C}_{2}}(t)$ ，得输出的葡萄糖质量是 $C2(t)⋅Δt⋅vf{{C}_{2}}(t)\cdot \Delta t\cdot {{v}_{f}}$ 。
输入液体体积是 $Δt⋅vf\Delta t\cdot {{v}_{f}}$ ，液体的浓度是 ${{C}_{1}}(t)$ ，得输入的葡萄糖质量是 $C1(t)⋅Δt⋅vf{{C}_{1}}\left( t \right)\cdot \Delta t\cdot {{v}_{f}}$ 。
液体的浓度 $C2(t+Δt)=C2(t)⋅V−C2(t)⋅Δt⋅vf+C1(t)⋅Δt⋅vfV{{C}_{2}}(t+\Delta t)=\frac{{{C}_{2}}(t)\cdot V-{{C}_{2}}(t)\cdot \Delta t\cdot {{v}_{f}}+{{C}_{1}}\left( t \right)\cdot \Delta t\cdot {{v}_{f}}}{V}$
$C2(t+Δt)−C2(t)=−C2(t)⋅Δt⋅vf+C1(t)⋅Δt⋅vfV{{C}_{2}}(t+\Delta t)-{{C}_{2}}(t)=\frac{-{{C}_{2}}(t)\cdot \Delta t\cdot {{v}_{f}}+{{C}_{1}}\left( t \right)\cdot \Delta t\cdot {{v}_{f}}}{V}$
$C2(t+Δt)−C2(t)Δt=−C2(t)⋅vf+C1(t)⋅vfV\frac{{{C}_{2}}(t+\Delta t)-{{C}_{2}}(t)}{\Delta t}=\frac{-{{C}_{2}}(t)\cdot {{v}_{f}}+{{C}_{1}}\left( t \right)\cdot {{v}_{f}}}{V}$
可得浓度变化的速度 $dC2dt=−vfVC2+vfVC1(t)\frac{d{{C}_{2}}}{dt}=-\frac{{{v}_{f}}}{V}{{C}_{2}}+\frac{{{v}_{f}}}{V}{{C}_{1}}\left( t \right)$
$dC2dt+vfVC2=vfVC1(t)\frac{d{{C}_{2}}}{dt}+\frac{{{v}_{f}}}{V}{{C}_{2}}=\frac{{{v}_{f}}}{V}{{C}_{1}}\left( t \right)$
$C2=ce−vfVt+e−vfVt⋅vfV⋅∫evfVt⋅(C01−C01e−vfVt)dt{{C}_{2}}=c{{e}^{-\frac{{{v}_{f}}}{V}t}}+{{e}^{-\frac{{{v}_{f}}}{V}t}}\cdot \frac{{{v}_{f}}}{V}\cdot \int{{{e}^{\frac{{{v}_{f}}}{V}t}}\cdot \left( {{C}_{01}}-{{C}_{01}}{{e}^{-\frac{{{v}_{f}}}{V}t}} \right)}dt$
$C2=ce−vfVt+e−vfVt⋅vfV⋅∫(C01evfVt−C01)dt{{C}_{2}}=c{{e}^{-\frac{{{v}_{f}}}{V}t}}+{{e}^{-\frac{{{v}_{f}}}{V}t}}\cdot \frac{{{v}_{f}}}{V}\cdot \int{\left( {{C}_{01}}{{e}^{\frac{{{v}_{f}}}{V}t}}-{{C}_{01}} \right)}dt$
$C2=ce−vfVt+e−vfVt⋅vfV⋅(C01⋅Vvf⋅evfVt−C01⋅t){{C}_{2}}=c{{e}^{-\frac{{{v}_{f}}}{V}t}}+{{e}^{-\frac{{{v}_{f}}}{V}t}}\cdot \frac{{{v}_{f}}}{V}\cdot \left( {{C}_{01}}\cdot \frac{V}{{{v}_{f}}}\cdot {{e}^{\frac{{{v}_{f}}}{V}t}}-{{C}_{01}}\cdot t \right)$
$C2=(ce−vfVt)+C01−(vfV⋅C01⋅te−vfVt)(2.1){{C}_{2}}=\left( c{{e}^{-\frac{{{v}_{f}}}{V}t}} \right)+{{C}_{01}}-\left( \frac{{{v}_{f}}}{V}\cdot {{C}_{01}}\cdot t{{e}^{-\frac{{{v}_{f}}}{V}t}} \right)\tag{2.1}$
将初值 $C2(0)=0{{C}_{2}}\left( 0 \right)=0$ 带入式（2.1）可得
$c=-{{C}_{01}}$
即 $C2=−C01e−vfVt−(vfV⋅C01⋅te−vfVt)+C01(2.2){{C}_{2}}=-{{C}_{01}}{{e}^{-\frac{{{v}_{f}}}{V}t}}-\left( \frac{{{v}_{f}}}{V}\cdot {{C}_{01}}\cdot t{{e}^{-\frac{{{v}_{f}}}{V}t}} \right)+{{C}_{01}}\tag{2.2}$

7.1.2.2 阶段2

令 $t^=t−T\hat{t}=t-T$ ，即阶段二从 $t^=0\hat{t}=0$ 开始，浓度 $C^2(t^)=C2(t^+T){{\hat{C}}_{2}}\left( {\hat{t}} \right)={{C}_{2}}\left( \hat{t}+T \right)$
初值是 $C^2(0)=C2(T)=−C01e−vfVT−(vfV⋅C01⋅Te−vfVT)+C01{{\hat{C}}_{2}}\left( 0 \right)={{C}_{2}}\left( \text{T} \right)=-{{C}_{01}}{{e}^{-\frac{{{v}_{f}}}{V}T}}-\left( \frac{{{v}_{f}}}{V}\cdot {{C}_{01}}\cdot T{{e}^{-\frac{{{v}_{f}}}{V}T}} \right)+{{C}_{01}}$
$C^2(t^+Δt^)=C^2(t^)⋅V−C^2(t^)⋅Δt^⋅vf+C^1(t^)⋅Δt^⋅vfV{{\hat{C}}_{2}}\left( \hat{t}+\Delta \hat{t} \right)=\frac{{{{\hat{C}}}_{2}}\left( {\hat{t}} \right)\cdot V-{{{\hat{C}}}_{2}}\left( {\hat{t}} \right)\cdot \Delta \hat{t}\cdot {{v}_{f}}+{{{\hat{C}}}_{1}}\left( {\hat{t}} \right)\cdot \Delta \hat{t}\cdot {{v}_{f}}}{V}$
$C^2(t^+Δt^)−C^2(t^)Δt^=−vfVC^2(t^)+vfVC^1(t^)\frac{{{{\hat{C}}}_{2}}\left( \hat{t}+\Delta \hat{t} \right)-{{{\hat{C}}}_{2}}\left( {\hat{t}} \right)}{\Delta \hat{t}}=-\frac{{{v}_{f}}}{V}{{\hat{C}}_{2}}\left( {\hat{t}} \right)+\frac{{{v}_{f}}}{V}{{\hat{C}}_{1}}\left( {\hat{t}} \right)$
可得浓度变化的速度 $dC^2dt^=−vfVC^2+vfVC^1(t^)\frac{d{{{\hat{C}}}_{2}}}{d\hat{t}}=-\frac{{{v}_{f}}}{V}{{\hat{C}}_{2}}+\frac{{{v}_{f}}}{V}{{\hat{C}}_{1}}\left( {\hat{t}} \right)$
$dC^2dt^+vfVC^2=vfVC^1(t^)\frac{d{{{\hat{C}}}_{2}}}{d\hat{t}}+\frac{{{v}_{f}}}{V}{{\hat{C}}_{2}}=\frac{{{v}_{f}}}{V}{{\hat{C}}_{1}}\left( {\hat{t}} \right)$
$C^2=ce−vfVt^+C1(T)⋅e−vfVt^⋅vfV⋅∫evfVt^(e−vfVt^)dt^{{\hat{C}}_{2}}=c{{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}}+{{C}_{1}}\left( T \right)\cdot {{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}}\cdot \frac{{{v}_{f}}}{V}\cdot \int{{{e}^{\frac{{{v}_{f}}}{V}\hat{t}}}}\left( {{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}} \right)d\hat{t}$
$C^2=ce−vfVt^+C1(T)⋅vfV⋅t^e−vfVt^(2.3){{\hat{C}}_{2}}=c{{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}}+{{C}_{1}}\left( T \right)\cdot \frac{{{v}_{f}}}{V}\cdot \hat{t}{{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}}\tag{2.3}$
将初值代入式（2.3）得 $c=C2(T)c={{C}_{2}}\left( T \right)$
得 $C^2=C2(T)e−vfVt^+C1(T)⋅vfV⋅te−vfVt^(2.4){{\hat{C}}_{2}}={{C}_{2}}\left( T \right){{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}}+{{C}_{1}}\left( T \right)\cdot \frac{{{v}_{f}}}{V}\cdot t{{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}}\tag{2.4}$

7.1.2.3 结果

由式（2.2）和式（2.4）可得
${C2=−C01e−vfVt−(vfV⋅C01⋅te−vfVt)+C01t≤T=0.05vfC^2=C2(T)e−vfVt^+C1(T)⋅vfV⋅t^e−vfVt^t>T\left\{ \begin{matrix} {{C}_{2}}=-{{C}_{01}}{{e}^{-\frac{{{v}_{f}}}{V}t}}-\left( \frac{{{v}_{f}}}{V}\cdot {{C}_{01}}\cdot t{{e}^{-\frac{{{v}_{f}}}{V}t}} \right)+{{C}_{01}} & t\le T=\frac{0.05}{{{v}_{f}}} \\ {{{\hat{C}}}_{2}}={{C}_{2}}\left( T \right){{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}}+{{C}_{1}}\left( T \right)\cdot \frac{{{v}_{f}}}{V}\cdot \hat{t}{{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}} & t>T \\ \end{matrix} \right.$
即
${C2=−C01e−vfVt−(vfV⋅C01⋅te−vfVt)+C01t≤T=0.05vfC2=C2(T)e−vfV(t−T)+C1(T)⋅vfV⋅(t−T)e−vfV(t−T)t>T\left\{ \begin{matrix} {{C}_{2}}=-{{C}_{01}}{{e}^{-\frac{{{v}_{f}}}{V}t}}-\left( \frac{{{v}_{f}}}{V}\cdot {{C}_{01}}\cdot t{{e}^{-\frac{{{v}_{f}}}{V}t}} \right)+{{C}_{01}} & t\le T=\frac{0.05}{{{v}_{f}}} \\ {{C}_{2}}={{C}_{2}}\left( T \right){{e}^{-\frac{{{v}_{f}}}{V}\left( t-T \right)}}+{{C}_{1}}\left( T \right)\cdot \frac{{{v}_{f}}}{V}\cdot \left( t-T \right){{e}^{-\frac{{{v}_{f}}}{V}\left( t-T \right)}} & t>T \\ \end{matrix} \right.$

7.1.3 反应池3

反应池3液体浓度变化也分为两个阶段，和反应池1一一对应。

7.1.3.1 阶段一

考虑一个很短的时间 $Δt\Delta t$ 内，
输出液体体积是 $Δt⋅vf\Delta t\cdot {{v}_{f}}$ ，液体的浓度是 ${{C}_{3}}(t)$ ，得输出的葡萄糖质量是 $C3(t)⋅Δt⋅vf{{C}_{3}}(t)\cdot \Delta t\cdot {{v}_{f}}$ 。
输入液体体积是 $Δt⋅vf\Delta t\cdot {{v}_{f}}$ ，液体的浓度是 ${{C}_{2}}(t)$ ，得输入的葡萄糖质量是 $C2(t)⋅Δt⋅vf{{C}_{2}}\left( t \right)\cdot \Delta t\cdot {{v}_{f}}$ 。
液体的浓度 $C3(t+Δt)=C3(t)⋅V−C3(t)⋅Δt⋅vf+C2(t)⋅Δt⋅vfV{{C}_{3}}(t+\Delta t)=\frac{{{C}_{3}}(t)\cdot V-{{C}_{3}}(t)\cdot \Delta t\cdot {{v}_{f}}+{{C}_{2}}\left( t \right)\cdot \Delta t\cdot {{v}_{f}}}{V}$
$C3(t+Δt)−C3(t)=−C3(t)⋅Δt⋅vf+C2(t)⋅Δt⋅vfV{{C}_{3}}(t+\Delta t)-{{C}_{3}}(t)=\frac{-{{C}_{3}}(t)\cdot \Delta t\cdot {{v}_{f}}+{{C}_{2}}\left( t \right)\cdot \Delta t\cdot {{v}_{f}}}{V}$
$C3(t+Δt)−C3(t)Δt=−vfVC3(t)+vfVC2(t)\frac{{{C}_{3}}(t+\Delta t)-{{C}_{3}}(t)}{\Delta t}=-\frac{{{v}_{f}}}{V}{{C}_{3}}(t)+\frac{{{v}_{f}}}{V}{{C}_{2}}\left( t \right)$
可得浓度变化的速度 $dC3dt+vfVC3=vfVC2(t)\frac{d{{C}_{3}}}{dt}+\frac{{{v}_{f}}}{V}{{C}_{3}}=\frac{{{v}_{f}}}{V}{{C}_{2}}\left( t \right)$
$C3=ce−vfVt+e−vfVt⋅vfV⋅∫evfVt⋅(−C01e−vfVt−(vfV⋅C01⋅te−vfVt)+C01)dt{{C}_{3}}=c{{e}^{-\frac{{{v}_{f}}}{V}t}}+{{e}^{-\frac{{{v}_{f}}}{V}t}}\cdot \frac{{{v}_{f}}}{V}\cdot \int{{{e}^{\frac{{{v}_{f}}}{V}t}}\cdot \left( -{{C}_{01}}{{e}^{-\frac{{{v}_{f}}}{V}t}}-\left( \frac{{{v}_{f}}}{V}\cdot {{C}_{01}}\cdot t{{e}^{-\frac{{{v}_{f}}}{V}t}} \right)+{{C}_{01}} \right)}dt$
$C3=ce−vfVt+e−vfVt⋅vfV⋅∫(−C01−vfV⋅C01⋅t+C01⋅evfVt)dt{{C}_{3}}=c{{e}^{-\frac{{{v}_{f}}}{V}t}}+{{e}^{-\frac{{{v}_{f}}}{V}t}}\cdot \frac{{{v}_{f}}}{V}\cdot \int{\left( -{{C}_{01}}-\frac{{{v}_{f}}}{V}\cdot {{C}_{01}}\cdot t+{{C}_{01}}\cdot {{e}^{\frac{{{v}_{f}}}{V}t}} \right)}dt$
$C3=ce−vfVt+e−vfVt⋅vfV⋅(−C01t−vf2V⋅C01⋅t2+C01⋅Vvf⋅evfVt){{C}_{3}}=c{{e}^{-\frac{{{v}_{f}}}{V}t}}+{{e}^{-\frac{{{v}_{f}}}{V}t}}\cdot \frac{{{v}_{f}}}{V}\cdot \left( -{{C}_{01}}t-\frac{{{v}_{f}}}{2V}\cdot {{C}_{01}}\cdot {{t}^{2}}+{{C}_{01}}\cdot \frac{V}{{{v}_{f}}}\cdot {{e}^{\frac{{{v}_{f}}}{V}t}} \right)$
$C3=ce−vfVt−C01⋅vfVt⋅e−vfVt−C01⋅vf22V2⋅t2⋅e−vfVt+C01(3.1){{C}_{3}}=c{{e}^{-\frac{{{v}_{f}}}{V}t}}-{{C}_{01}}\cdot \frac{{{v}_{f}}}{V}t\cdot {{e}^{-\frac{{{v}_{f}}}{V}t}}-{{C}_{01}}\cdot \frac{v_{f}^{2}}{2{{V}^{2}}}\cdot {{t}^{2}}\cdot {{e}^{-\frac{{{v}_{f}}}{V}t}}+{{C}_{01}}\tag{3.1}$
将初值 $C3(0)=0{{C}_{3}}\left( 0 \right)=0$ 带入式（3.1）可得
$c=-{{C}_{01}}$
即 $C3=−C01e−vfVt−C01⋅vfVt⋅e−vfVt−C01⋅vf22V2⋅t2⋅e−vfVt+C01(3.2){{C}_{3}}=-{{C}_{01}}{{e}^{-\frac{{{v}_{f}}}{V}t}}-{{C}_{01}}\cdot \frac{{{v}_{f}}}{V}t\cdot {{e}^{-\frac{{{v}_{f}}}{V}t}}-{{C}_{01}}\cdot \frac{v_{f}^{2}}{2{{V}^{2}}}\cdot {{t}^{2}}\cdot {{e}^{-\frac{{{v}_{f}}}{V}t}}+{{C}_{01}}\tag{3.2}$

7.1.3.2 阶段二

令 $t^=t−T\hat{t}=t-T$ ，即阶段二从 $t^=0\hat{t}=0$ 开始，浓度 $C^3(t^)=C3(t^+T){{\hat{C}}_{3}}\left( {\hat{t}} \right)={{C}_{3}}\left( \hat{t}+T \right)$
初值是 $C^3(0)=C3(T){{\hat{C}}_{3}}\left( 0 \right)={{C}_{3}}\left( \text{T} \right)$
$C^3(t^+Δt^)=C^3(t^)⋅V−C^3(t^)⋅Δt^⋅vf+C^2(t^)⋅Δt^⋅vfV{{\hat{C}}_{3}}\left( \hat{t}+\Delta \hat{t} \right)=\frac{{{{\hat{C}}}_{3}}\left( {\hat{t}} \right)\cdot V-{{{\hat{C}}}_{3}}\left( {\hat{t}} \right)\cdot \Delta \hat{t}\cdot {{v}_{f}}+{{{\hat{C}}}_{2}}\left( {\hat{t}} \right)\cdot \Delta \hat{t}\cdot {{v}_{f}}}{V}$
$C^2(t^+Δt^)−C^2(t^)Δt^=−vfVC^2(t^)+vfVC^1(t^)\frac{{{{\hat{C}}}_{2}}\left( \hat{t}+\Delta \hat{t} \right)-{{{\hat{C}}}_{2}}\left( {\hat{t}} \right)}{\Delta \hat{t}}=-\frac{{{v}_{f}}}{V}{{\hat{C}}_{2}}\left( {\hat{t}} \right)+\frac{{{v}_{f}}}{V}{{\hat{C}}_{1}}\left( {\hat{t}} \right)$
$C^3(t^+Δt^)−C^3(t^)Δt^=−vfVC^3(t^)+vfVC^2(t^)\frac{{{{\hat{C}}}_{3}}\left( \hat{t}+\Delta \hat{t} \right)-{{{\hat{C}}}_{3}}\left( {\hat{t}} \right)}{\Delta \hat{t}}=-\frac{{{v}_{f}}}{V}{{\hat{C}}_{3}}\left( {\hat{t}} \right)+\frac{{{v}_{f}}}{V}{{\hat{C}}_{2}}\left( {\hat{t}} \right)$
可得浓度变化的速度 $dC^3dt^+vfVC^3=vfVC^2(t^)\frac{d{{{\hat{C}}}_{3}}}{d\hat{t}}+\frac{{{v}_{f}}}{V}{{\hat{C}}_{3}}=\frac{{{v}_{f}}}{V}{{\hat{C}}_{2}}\left( {\hat{t}} \right)$
$C^3=ce−vfVt^+e−vfVt^⋅vfV⋅∫evfVt^(C2(T)e−vfVt^+C1(T)⋅vfV⋅t^e−vfVt^)dt^{{\hat{C}}_{3}}=c{{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}}+{{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}}\cdot \frac{{{v}_{f}}}{V}\cdot \int{{{e}^{\frac{{{v}_{f}}}{V}\hat{t}}}}\left( {{C}_{2}}\left( T \right){{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}}+{{C}_{1}}\left( T \right)\cdot \frac{{{v}_{f}}}{V}\cdot \hat{t}{{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}} \right)d\hat{t}$
$C^3=ce−vfVt^+e−vfVt^⋅vfV⋅∫(C2(T)+C1(T)⋅vfV⋅t^)dt^{{\hat{C}}_{3}}=c{{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}}+{{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}}\cdot \frac{{{v}_{f}}}{V}\cdot \int{\left( {{C}_{2}}\left( T \right)+{{C}_{1}}\left( T \right)\cdot \frac{{{v}_{f}}}{V}\cdot \hat{t} \right)}d\hat{t}$
$C^3=ce−vfVt^+C2(T)⋅vfV⋅te−vfVt^+C1(T)⋅vf22V2⋅t^2e−vfVt^(3.3){{\hat{C}}_{3}}=c{{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}}+{{C}_{2}}\left( T \right)\cdot \frac{{{v}_{f}}}{V}\cdot t{{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}}+{{C}_{1}}\left( T \right)\cdot \frac{v_{f}^{2}}{2{{V}^{2}}}\cdot {{\hat{t}}^{2}}{{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}}\tag{3.3}$
将初值代入式（3.3）得 $c=C3(T)c={{C}_{3}}\left( T \right)$
得 $C^3=C3(T)e−vfVt^+C2(T)⋅vfV⋅te−vfVt^+C1(T)⋅vf22V2⋅t^2e−vfVt^(3.4){{\hat{C}}_{3}}={{C}_{3}}\left( T \right){{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}}+{{C}_{2}}\left( T \right)\cdot \frac{{{v}_{f}}}{V}\cdot t{{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}}+{{C}_{1}}\left( T \right)\cdot \frac{v_{f}^{2}}{2{{V}^{2}}}\cdot {{\hat{t}}^{2}}{{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}}\tag{3.4}$

7.1.3.3 结果

由式（3.2）和式（3.4）可得
${C3=−C01e−vfVt−C01⋅vfVt⋅e−vfVt−C01⋅vf22V2⋅t2⋅e−vfVt+C01t≤T=0.05vfC^3=C3(T)e−vfVt^+C2(T)⋅vfV⋅te−vfVt^+C1(T)⋅vf22V2⋅t^2e−vfVt^t>T\left\{ \begin{matrix} {{C}_{3}}=-{{C}_{01}}{{e}^{-\frac{{{v}_{f}}}{V}t}}-{{C}_{01}}\cdot \frac{{{v}_{f}}}{V}t\cdot {{e}^{-\frac{{{v}_{f}}}{V}t}}-{{C}_{01}}\cdot \frac{v_{f}^{2}}{2{{V}^{2}}}\cdot {{t}^{2}}\cdot {{e}^{-\frac{{{v}_{f}}}{V}t}}+{{C}_{01}} & t\le T=\frac{0.05}{{{v}_{f}}} \\ {{{\hat{C}}}_{3}}={{C}_{3}}\left( T \right){{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}}+{{C}_{2}}\left( T \right)\cdot \frac{{{v}_{f}}}{V}\cdot t{{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}}+{{C}_{1}}\left( T \right)\cdot \frac{v_{f}^{2}}{2{{V}^{2}}}\cdot {{{\hat{t}}}^{2}}{{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}} & t>T \\ \end{matrix} \right.$
即
${C3=−C01e−vfVt−C01⋅vfVt⋅e−vfVt−C01⋅vf22V2⋅t2⋅e−vfVt+C01t≤T=0.05vfC3=C3(T)e−vfV(t−T)+C2(T)⋅vfV⋅(t−T)e−vfV(t−T)+C1(T)⋅vf22V2⋅(t−T)2e−vfV(t−T)t>T\left\{ \begin{matrix} {{C}_{3}}=-{{C}_{01}}{{e}^{-\frac{{{v}_{f}}}{V}t}}-{{C}_{01}}\cdot \frac{{{v}_{f}}}{V}t\cdot {{e}^{-\frac{{{v}_{f}}}{V}t}}-{{C}_{01}}\cdot \frac{v_{f}^{2}}{2{{V}^{2}}}\cdot {{t}^{2}}\cdot {{e}^{-\frac{{{v}_{f}}}{V}t}}+{{C}_{01}} & t\le T=\frac{0.05}{{{v}_{f}}} \\ {{C}_{3}}={{C}_{3}}\left( T \right){{e}^{-\frac{{{v}_{f}}}{V}\left( t-T \right)}}+{{C}_{2}}\left( T \right)\cdot \frac{{{v}_{f}}}{V}\cdot \left( t-T \right){{e}^{-\frac{{{v}_{f}}}{V}\left( t-T \right)}}+{{C}_{1}}\left( T \right)\cdot \frac{v_{f}^{2}}{2{{V}^{2}}}\cdot {{\left( t-T \right)}^{2}}{{e}^{-\frac{{{v}_{f}}}{V}\left( t-T \right)}} & t>T \\ \end{matrix} \right.$