7.1.4 结果
{C1(t)=−C01e−vfVt+C01t≤T=0.05vfC1(t)=C1(T)⋅e−vfV(t−T)t>T\left\{ \begin{matrix}
{{C}_{1}}\left( t \right)=-{{C}_{01}}{{e}^{-\frac{{{v}_{f}}}{V}t}}+{{C}_{01}} & t\le T=\frac{0.05}{{{v}_{f}}} \\
{{C}_{1}}\left( t \right)={{C}_{1}}\left( T \right)\cdot {{e}^{-\frac{{{v}_{f}}}{V}\left( t-T \right)}} & t>T \\
\end{matrix} \right.{C1(t)=−C01e−Vvft+C01C1(t)=C1(T)⋅e−Vvf(t−T)t≤T=vf0.05t>T
{C2(t)=−C01e−vfVt−vfV⋅C01⋅te−vfVt+C01t≤T=0.05vfC2(t)=C2(T)e−vfV(t−T)+C1(T)⋅vfV⋅(t−T)e−vfV(t−T)t>T\left\{ \begin{matrix}
{{C}_{2}}\left( t \right)=-{{C}_{01}}{{e}^{-\frac{{{v}_{f}}}{V}t}}-\frac{{{v}_{f}}}{V}\cdot {{C}_{01}}\cdot t{{e}^{-\frac{{{v}_{f}}}{V}t}}+{{C}_{01}} & t\le T=\frac{0.05}{{{v}_{f}}} \\
{{C}_{2}}\left( t \right)={{C}_{2}}\left( T \right){{e}^{-\frac{{{v}_{f}}}{V}\left( t-T \right)}}+{{C}_{1}}\left( T \right)\cdot \frac{{{v}_{f}}}{V}\cdot \left( t-T \right){{e}^{-\frac{{{v}_{f}}}{V}\left( t-T \right)}} & t>T \\
\end{matrix} \right.{C2(t)=−C01e−Vvft−Vvf⋅C01⋅te−Vvft+C01C2(t)=C2(T)e−Vvf(t−T)+C1(T)⋅Vvf⋅(t−T)e−Vvf(t−T)t≤T=vf0.05t>T
{C3(t)=−C01e−vfVt−C01⋅vfVt⋅e−vfVt−C01⋅vf22V2⋅t2⋅e−vfVt+C01t≤T=0.05vfC3(t)=C3(T)e−vfV(t−T)+C2(T)⋅vfV⋅(t−T)e−vfV(t−T)+C1(T)⋅vf22V2⋅(t−T)2e−vfV(t−T)t>T\left\{ \begin{matrix}
{{C}_{3}}\left( t \right)=-{{C}_{01}}{{e}^{-\frac{{{v}_{f}}}{V}t}}-{{C}_{01}}\cdot \frac{{{v}_{f}}}{V}t\cdot {{e}^{-\frac{{{v}_{f}}}{V}t}}-{{C}_{01}}\cdot \frac{v_{f}^{2}}{2{{V}^{2}}}\cdot {{t}^{2}}\cdot {{e}^{-\frac{{{v}_{f}}}{V}t}}+{{C}_{01}} & t\le T=\frac{0.05}{{{v}_{f}}} \\
{{C}_{3}}\left( t \right)={{C}_{3}}\left( T \right){{e}^{-\frac{{{v}_{f}}}{V}\left( t-T \right)}}+{{C}_{2}}\left( T \right)\cdot \frac{{{v}_{f}}}{V}\cdot \left( t-T \right){{e}^{-\frac{{{v}_{f}}}{V}\left( t-T \right)}}+{{C}_{1}}\left( T \right)\cdot \frac{v_{f}^{2}}{2{{V}^{2}}}\cdot {{\left( t-T \right)}^{2}}{{e}^{-\frac{{{v}_{f}}}{V}\left( t-T \right)}} & t>T \\
\end{matrix} \right.⎩⎨⎧C3(t)=−C01e−Vvft−C01⋅Vvft⋅e−Vvft−C01⋅2V2vf2⋅t2⋅e−Vvft+C01C3(t)=C3(T)e−Vvf(t−T)+C2(T)⋅Vvf⋅(t−T)e−Vvf(t−T)+C1(T)⋅2V2vf2⋅(t−T)2e−Vvf(t−T)t≤T=vf0.05t>T
写成下面的形式,MATLAB编程方便一点
{C1(t)=(−e−vfVt+1)C01t≤T=0.05vfC1(t)=C1(T)⋅e−vfV(t−T)t>T\left\{ \begin{matrix}
{{C}_{1}}\left( t \right)=\left( -{{e}^{-\frac{{{v}_{f}}}{V}t}}+1 \right){{C}_{01}} & t\le T=\frac{0.05}{{{v}_{f}}} \\
{{C}_{1}}\left( t \right)={{C}_{1}}\left( T \right)\cdot {{e}^{-\frac{{{v}_{f}}}{V}\left( t-T \right)}} & t>T \\
\end{matrix} \right.{C1(t)=(−e−Vvft+1)C01C1(t)=C1(T)⋅e−Vvf(t−T)t≤T=vf0.05t>T
{C2(t)=((−1−vfV⋅t)e−vfVt+1)C01t≤T=0.05vfC2(t)=(C2(T)+C1(T)⋅vfV⋅(t−T))e−vfV(t−T)t>T\left\{ \begin{matrix}
{{C}_{2}}\left( t \right)=\left( \left( -1-\frac{{{v}_{f}}}{V}\cdot t \right){{e}^{-\frac{{{v}_{f}}}{V}t}}+1 \right){{C}_{01}} & t\le T=\frac{0.05}{{{v}_{f}}} \\
{{C}_{2}}\left( t \right)=\left( {{C}_{2}}\left( T \right)+{{C}_{1}}\left( T \right)\cdot \frac{{{v}_{f}}}{V}\cdot \left( t-T \right) \right){{e}^{-\frac{{{v}_{f}}}{V}\left( t-T \right)}} & t>T \\
\end{matrix} \right.{C2(t)=((−1−Vvf⋅t)e−Vvft+1)C01C2(t)=(C2(T)+C1(T)⋅Vvf⋅(t−T))e−Vvf(t−T)t≤T=vf0.05t>T
{C3(t)=((−1−vfVt−vf22V2⋅t2)⋅e−vfVt+1)C01t≤T=0.05vfC3(t)=(C3(T)+C2(T)⋅vfV⋅(t−T)+C1(T)⋅vf22V2⋅(t−T)2)e−vfV(t−T)t>T\left\{ \begin{matrix}
{{C}_{3}}\left( t \right)=\left( \left( -1-\frac{{{v}_{f}}}{V}t-\frac{v_{f}^{2}}{2{{V}^{2}}}\cdot {{t}^{2}} \right)\cdot {{e}^{-\frac{{{v}_{f}}}{V}t}}+1 \right){{C}_{01}} & t\le T=\frac{0.05}{{{v}_{f}}} \\
{{C}_{3}}\left( t \right)=\left( {{C}_{3}}\left( T \right)+{{C}_{2}}\left( T \right)\cdot \frac{{{v}_{f}}}{V}\cdot \left( t-T \right)+{{C}_{1}}\left( T \right)\cdot \frac{v_{f}^{2}}{2{{V}^{2}}}\cdot {{\left( t-T \right)}^{2}} \right){{e}^{-\frac{{{v}_{f}}}{V}\left( t-T \right)}} & t>T \\
\end{matrix} \right.⎩⎨⎧C3(t)=((−1−Vvft−2V2vf2⋅t2)⋅e−Vvft+1)C01C3(t)=(C3(T)+C2(T)⋅Vvf⋅(t−T)+C1(T)⋅2V2vf2⋅(t−T)2)e−Vvf(t−T)t≤T=vf0.05t>T
7.2 高阶常微分解法
7.2.1 反应池1
和解法一的步骤一致。
7.2.2 反应池2
7.2.2.1 阶段一
由解法一可得,dC2dt+vfVC2=vfVC1(t)\frac{d{{C}_{2}}}{dt}+\frac{{{v}_{f}}}{V}{{C}_{2}}=\frac{{{v}_{f}}}{V}{{C}_{1}}\left( t \right)dtdC2+VvfC2=VvfC1(t)
两边微分d2dt2C2+vfV⋅ddtC2=vfV⋅ddtC1\frac{{{d}^{2}}}{d{{t}^{2}}}{{C}_{2}}+\frac{{{v}_{f}}}{V}\cdot \frac{d}{dt}{{C}_{2}}=\frac{{{v}_{f}}}{V}\cdot \frac{d}{dt}{{C}_{1}}dt2d2C2+Vvf⋅dtdC2=Vvf⋅dtdC1
由C1=−C01e−vfVt+C01{{C}_{1}}=-{{C}_{01}}{{e}^{-\frac{{{v}_{f}}}{V}t}}+{{C}_{01}}C1=−C01e−Vvft+C01得到ddtC1=C01vfV⋅e−vfVt\frac{d}{dt}{{C}_{1}}={{C}_{01}}\frac{{{v}_{f}}}{V}\cdot {{e}^{-\frac{{{v}_{f}}}{V}t}}dtdC1=C01Vvf⋅e−Vvft,带入上式,得
d2dt2C2+vfV⋅ddtC2=C01⋅vf2V2⋅e−vfVt\frac{{{d}^{2}}}{d{{t}^{2}}}{{C}_{2}}+\frac{{{v}_{f}}}{V}\cdot \frac{d}{dt}{{C}_{2}}={{C}_{01}}\cdot \frac{v_{f}^{2}}{{{V}^{2}}}\cdot {{e}^{-\frac{{{v}_{f}}}{V}t}}dt2d2C2+Vvf⋅dtdC2=C01⋅V2vf2⋅e−Vvft
首先求齐次解d2dt2C2c+vfV⋅ddtC2c=0\frac{{{d}^{2}}}{d{{t}^{2}}}{{C}_{2c}}+\frac{{{v}_{f}}}{V}\cdot \frac{d}{dt}{{C}_{2c}}=0dt2d2C2c+Vvf⋅dtdC2c=0
列出辅助方程m2+vfVm=0{{m}^{2}}+\frac{{{v}_{f}}}{V}m=0m2+Vvfm=0
解得{m1=0m2=−vfV\left\{ \begin{matrix}
{{m}_{1}}=0 \\
{{m}_{2}}=-\frac{{{v}_{f}}}{V} \\
\end{matrix} \right.{m1=0m2=−Vvf
齐次解C2c=c1+c2e−vfVt{{C}_{2c}}={{c}_{1}}+{{c}_{2}}{{e}^{-\frac{{{v}_{f}}}{V}t}}C2c=c1+c2e−Vvft
令特解C2p=Ate−vfVt{{C}_{2p}}=At{{e}^{-\frac{{{v}_{f}}}{V}t}}C2p=Ate−Vvft
得{dC2pdt=−vfVAte−vfVt+Ae−vfVtd2C2pdt2=vf2V2Ate−vfVt−2vfVAe−vfVt\left\{ \begin{matrix}
\frac{d{{C}_{2p}}}{dt}=-\frac{{{v}_{f}}}{V}At{{e}^{-\frac{{{v}_{f}}}{V}t}}+A{{e}^{-\frac{{{v}_{f}}}{V}t}} \\
\frac{{{d}^{2}}{{C}_{2p}}}{d{{t}^{2}}}=\frac{v_{f}^{2}}{{{V}^{2}}}At{{e}^{-\frac{{{v}_{f}}}{V}t}}-2\frac{{{v}_{f}}}{V}A{{e}^{-\frac{{{v}_{f}}}{V}t}} \\
\end{matrix} \right.{dtdC2p=−VvfAte−Vvft+Ae−Vvftdt2d2C2p=V2vf2Ate−Vvft−2VvfAe−Vvft
带入二阶微分方程得vf2V2Ate−vfVt−2vfVAe−vfVt+vfV(−vfVAte−vfVt+Ae−vfVt)=C01⋅vf2V2⋅e−vfVt\frac{v_{f}^{2}}{{{V}^{2}}}At{{e}^{-\frac{{{v}_{f}}}{V}t}}-2\frac{{{v}_{f}}}{V}A{{e}^{-\frac{{{v}_{f}}}{V}t}}+\frac{{{v}_{f}}}{V}\left( -\frac{{{v}_{f}}}{V}At{{e}^{-\frac{{{v}_{f}}}{V}t}}+A{{e}^{-\frac{{{v}_{f}}}{V}t}} \right)={{C}_{01}}\cdot \frac{v_{f}^{2}}{{{V}^{2}}}\cdot {{e}^{-\frac{{{v}_{f}}}{V}t}}V2vf2Ate−Vvft−2VvfAe−Vvft+Vvf(−VvfAte−Vvft+Ae−Vvft)=C01⋅V2vf2⋅e−Vvft
vf2V2At−2vfVA+−vf2V2At+vfVA=C01⋅vf2V2\frac{v_{f}^{2}}{{{V}^{2}}}At-2\frac{{{v}_{f}}}{V}A+-\frac{v_{f}^{2}}{{{V}^{2}}}At+\frac{{{v}_{f}}}{V}A={{C}_{01}}\cdot \frac{v_{f}^{2}}{{{V}^{2}}}V2vf2At−2VvfA+−V2vf2At+VvfA=C01⋅V2vf2
−vfVA=C01⋅vf2V2-\frac{{{v}_{f}}}{V}A={{C}_{01}}\cdot \frac{v_{f}^{2}}{{{V}^{2}}}−VvfA=C01⋅V2vf2
A=−C01⋅vfVA=-{{C}_{01}}\cdot \frac{{{v}_{f}}}{V}A=−C01⋅Vvf
因此通解C2=C2c+C2p=c1+c2e−vfVt−vfV⋅C01⋅te−vfVt{{C}_{2}}={{C}_{2c}}+{{C}_{2p}}={{c}_{1}}+{{c}_{2}}{{e}^{-\frac{{{v}_{f}}}{V}t}}-\frac{{{v}_{f}}}{V}\cdot {{C}_{01}}\cdot t{{e}^{-\frac{{{v}_{f}}}{V}t}}C2=C2c+C2p=c1+c2e−Vvft−Vvf⋅C01⋅te−Vvft
利用初值C2(0)=0{{C}_{2}}\left( 0 \right)=0C2(0)=0,解出c2=−c1{{c}_{2}}=-{{c}_{1}}c2=−c1
即C2=c1−c1e−vfVt−vfV⋅C01⋅te−vfVt{{C}_{2}}={{c}_{1}}-{{c}_{1}}{{e}^{-\frac{{{v}_{f}}}{V}t}}-\frac{{{v}_{f}}}{V}\cdot {{C}_{01}}\cdot t{{e}^{-\frac{{{v}_{f}}}{V}t}}C2=c1−c1e−Vvft−Vvf⋅C01⋅te−Vvft
ddtC2=vfVc1e−vfVt+vf2V2⋅C01⋅te−vfVt−vfV⋅C01e−vfVt\frac{d}{dt}{{C}_{2}}=\frac{{{v}_{f}}}{V}{{c}_{1}}{{e}^{-\frac{{{v}_{f}}}{V}t}}+\frac{v_{f}^{2}}{{{V}^{2}}}\cdot {{C}_{01}}\cdot t{{e}^{-\frac{{{v}_{f}}}{V}t}}-\frac{{{v}_{f}}}{V}\cdot {{C}_{01}}{{e}^{-\frac{{{v}_{f}}}{V}t}}dtdC2=Vvfc1e−Vvft+V2vf2⋅C01⋅te−Vvft−Vvf⋅C01e−Vvft
利用初值C2(0)=0{{C}_{2}}\left( 0 \right)=0C2(0)=0,解出c2=−c1{{c}_{2}}=-{{c}_{1}}c2=−c1
即C2=c1−c1e−vfVt−vfV⋅C01⋅te−vfVt{{C}_{2}}={{c}_{1}}-{{c}_{1}}{{e}^{-\frac{{{v}_{f}}}{V}t}}-\frac{{{v}_{f}}}{V}\cdot {{C}_{01}}\cdot t{{e}^{-\frac{{{v}_{f}}}{V}t}}C2=c1−c1e−Vvft−Vvf⋅C01⋅te−Vvft
ddtC2=vfVc1e−vfVt+vf2V2⋅C01⋅te−vfVt−vfV⋅C01e−vfVt\frac{d}{dt}{{C}_{2}}=\frac{{{v}_{f}}}{V}{{c}_{1}}{{e}^{-\frac{{{v}_{f}}}{V}t}}+\frac{v_{f}^{2}}{{{V}^{2}}}\cdot {{C}_{01}}\cdot t{{e}^{-\frac{{{v}_{f}}}{V}t}}-\frac{{{v}_{f}}}{V}\cdot {{C}_{01}}{{e}^{-\frac{{{v}_{f}}}{V}t}}dtdC2=Vvfc1e−Vvft+V2vf2⋅C01⋅te−Vvft−Vvf⋅C01e−Vvft
利用初值dC2(0)dt=−vfVC2(0)+vfVC1(0)=0\frac{d{{C}_{2}}\left( 0 \right)}{dt}=-\frac{{{v}_{f}}}{V}{{C}_{2}}\left( 0 \right)+\frac{{{v}_{f}}}{V}{{C}_{1}}\left( 0 \right)=0dtdC2(0)=−VvfC2(0)+VvfC1(0)=0
解得c1=C01{{c}_{1}}={{C}_{01}}c1=C01
C2=C01−C01e−vfVt−vfV⋅C01⋅te−vfVt{{C}_{2}}={{C}_{01}}-{{C}_{01}}{{e}^{-\frac{{{v}_{f}}}{V}t}}-\frac{{{v}_{f}}}{V}\cdot {{C}_{01}}\cdot t{{e}^{-\frac{{{v}_{f}}}{V}t}}C2=C01−C01e−Vvft−Vvf⋅C01⋅te−Vvft
7.2.2.2 阶段二
dC^2dt^+vfVC^2=vfVC^1(t^)\frac{d{{{\hat{C}}}_{2}}}{d\hat{t}}+\frac{{{v}_{f}}}{V}{{\hat{C}}_{2}}=\frac{{{v}_{f}}}{V}{{\hat{C}}_{1}}\left( {\hat{t}} \right)dt^dC^2+VvfC^2=VvfC^1(t^)
两边微分
d2dt^2C^2+vfVddt^C^2=vfVddt^C^1(t^)\frac{{{d}^{2}}}{d{{{\hat{t}}}^{2}}}{{\hat{C}}_{2}}+\frac{{{v}_{f}}}{V}\frac{d}{d\hat{t}}{{\hat{C}}_{2}}=\frac{{{v}_{f}}}{V}\frac{d}{d\hat{t}}{{\hat{C}}_{1}}\left( {\hat{t}} \right)dt^2d2C^2+Vvfdt^dC^2=Vvfdt^dC^1(t^)
由C^1(t^)=C1(T)⋅e−vfVt^{{\hat{C}}_{1}}\left( {\hat{t}} \right)={{C}_{1}}\left( T \right)\cdot {{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}}C^1(t^)=C1(T)⋅e−Vvft^得到ddt^C^1(t^)=−vfVC1(T)⋅e−vfVt^\frac{d}{d\hat{t}}{{\hat{C}}_{1}}\left( {\hat{t}} \right)=-\frac{{{v}_{f}}}{V}{{C}_{1}}\left( T \right)\cdot {{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}}dt^dC^1(t^)=−VvfC1(T)⋅e−Vvft^,带入上式,可得
d2dt^2C^2+vfVddt^C^2=−vf2V2C1(T)⋅e−vfVt^\frac{{{d}^{2}}}{d{{{\hat{t}}}^{2}}}{{\hat{C}}_{2}}+\frac{{{v}_{f}}}{V}\frac{d}{d\hat{t}}{{\hat{C}}_{2}}=-\frac{v_{f}^{2}}{{{V}^{2}}}{{C}_{1}}\left( T \right)\cdot {{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}}dt^2d2C^2+Vvfdt^dC^2=−V2vf2C1(T)⋅e−Vvft^
求出齐次解:C^2c=c1+c2e−vfVt^{{\hat{C}}_{2c}}={{c}_{1}}+{{c}_{2}}{{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}}C^2c=c1+c2e−Vvft^
令特解C^2p=At^e−vfVt^{{\hat{C}}_{2p}}=A\hat{t}{{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}}C^2p=At^e−Vvft^
得{dC^2pdt^=−vfVAt^e−vfVt^+Ae−vfVt^d2C^2pdt2=vf2V2At^e−vfVt^−2vfVAe−vfVt^\left\{ \begin{matrix}
\frac{d{{{\hat{C}}}_{2p}}}{d\hat{t}}=-\frac{{{v}_{f}}}{V}A\hat{t}{{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}}+A{{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}} \\
\frac{{{d}^{2}}{{{\hat{C}}}_{2p}}}{d{{t}^{2}}}=\frac{v_{f}^{2}}{{{V}^{2}}}A\hat{t}{{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}}-2\frac{{{v}_{f}}}{V}A{{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}} \\
\end{matrix} \right.{dt^dC^2p=−VvfAt^e−Vvft^+Ae−Vvft^dt2d2C^2p=V2vf2At^e−Vvft^−2VvfAe−Vvft^
d2dt^2C^2+vfVddt^C^2=−vf2V2C1(T)⋅e−vfVt^\frac{{{d}^{2}}}{d{{{\hat{t}}}^{2}}}{{\hat{C}}_{2}}+\frac{{{v}_{f}}}{V}\frac{d}{d\hat{t}}{{\hat{C}}_{2}}=-\frac{v_{f}^{2}}{{{V}^{2}}}{{C}_{1}}\left( T \right)\cdot {{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}}dt^2d2C^2+Vvfdt^dC^2=−V2vf2C1(T)⋅e−Vvft^
带入二阶微分方程得vf2V2At^e−vfVt^−2vfVAe−vfVt^+vfV(−vfVAt^e−vfVt^+Ae−vfVt^)=−vf2V2C1(T)⋅e−vfVt^\frac{v_{f}^{2}}{{{V}^{2}}}A\hat{t}{{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}}-2\frac{{{v}_{f}}}{V}A{{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}}+\frac{{{v}_{f}}}{V}\left( -\frac{{{v}_{f}}}{V}A\hat{t}{{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}}+A{{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}} \right)=-\frac{v_{f}^{2}}{{{V}^{2}}}{{C}_{1}}\left( T \right)\cdot {{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}}V2vf2At^e−Vvft^−2VvfAe−Vvft^+Vvf(−VvfAt^e−Vvft^+Ae−Vvft^)=−V2vf2C1(T)⋅e−Vvft^
−vfVA=−vf2V2C1(T)-\frac{{{v}_{f}}}{V}A=-\frac{v_{f}^{2}}{{{V}^{2}}}{{C}_{1}}\left( T \right)−VvfA=−V2vf2C1(T)
A=C1(T)vfVA={{C}_{1}}\left( T \right)\frac{{{v}_{f}}}{V}A=C1(T)Vvf
因此通解C^2=C^2c+C^2p=c1+c2e−vfVt^+vfV⋅C1(T)⋅t^e−vfVt^{{\hat{C}}_{2}}={{\hat{C}}_{2c}}+{{\hat{C}}_{2p}}={{c}_{1}}+{{c}_{2}}{{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}}+\frac{{{v}_{f}}}{V}\cdot {{C}_{1}}\left( T \right)\cdot \hat{t}{{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}}C^2=C^2c+C^2p=c1+c2e−Vvft^+Vvf⋅C1(T)⋅t^e−Vvft^
利用初值C^2(0)=C2(T){{\hat{C}}_{2}}\left( 0 \right)={{C}_{2}}\left( \text{T} \right)C^2(0)=C2(T),解出c1=C2(T)−c2{{c}_{1}}={{C}_{2}}\left( \text{T} \right)-{{c}_{2}}c1=C2(T)−c2
即C^2=C2(T)−c2+c2e−vfVt^+vfV⋅C1(T)⋅t^e−vfVt^{{\hat{C}}_{2}}={{C}_{2}}\left( \text{T} \right)-{{c}_{2}}+{{c}_{2}}{{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}}+\frac{{{v}_{f}}}{V}\cdot {{C}_{1}}\left( T \right)\cdot \hat{t}{{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}}C^2=C2(T)−c2+c2e−Vvft^+Vvf⋅C1(T)⋅t^e−Vvft^
ddtC^2=−vfVc2e−vfVt^+vfV⋅C1(T)⋅e−vfVt^−vf2V2⋅C1(T)⋅t^e−vfVt^\frac{d}{dt}{{\hat{C}}_{2}}=-\frac{{{v}_{f}}}{V}{{c}_{2}}{{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}}+\frac{{{v}_{f}}}{V}\cdot {{C}_{1}}\left( T \right)\cdot {{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}}-\frac{v_{f}^{2}}{{{V}^{2}}}\cdot {{C}_{1}}\left( T \right)\cdot \hat{t}{{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}}dtdC^2=−Vvfc2e−Vvft^+Vvf⋅C1(T)⋅e−Vvft^−V2vf2⋅C1(T)⋅t^e−Vvft^
利用初值dC^2(0)dt^=−vfVC^2(0)+vfVC^1(0)=−vfVC2(T)+vfVC1(T)\frac{d{{{\hat{C}}}_{2}}\left( 0 \right)}{d\hat{t}}=-\frac{{{v}_{f}}}{V}{{\hat{C}}_{2}}\left( 0 \right)+\frac{{{v}_{f}}}{V}{{\hat{C}}_{1}}\left( 0 \right)=-\frac{{{v}_{f}}}{V}{{C}_{2}}\left( T \right)+\frac{{{v}_{f}}}{V}{{C}_{1}}\left( T \right)dt^dC^2(0)=−VvfC^2(0)+VvfC^1(0)=−VvfC2(T)+VvfC1(T)
解读c2=C2(T){{c}_{2}}={{C}_{2}}\left( T \right)c2=C2(T)
C^2=C2(T)e−vfVt^+C1(T)⋅vfV⋅t^e−vfVt^{{\hat{C}}_{2}}={{C}_{2}}\left( T \right){{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}}+{{C}_{1}}\left( T \right)\cdot \frac{{{v}_{f}}}{V}\cdot \hat{t}{{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}}C^2=C2(T)e−Vvft^+C1(T)⋅Vvf⋅t^e−Vvft^
C^2=ce−vfVt^+C1(T)⋅e−vfVt^⋅vfV⋅∫evfVt^(e−vfVt^)dt^{{\hat{C}}_{2}}=c{{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}}+{{C}_{1}}\left( T \right)\cdot {{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}}\cdot \frac{{{v}_{f}}}{V}\cdot \int{{{e}^{\frac{{{v}_{f}}}{V}\hat{t}}}}\left( {{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}} \right)d\hat{t}C^2=ce−Vvft^+C1(T)⋅e−Vvft^⋅Vvf⋅∫eVvft^(e−Vvft^)dt^
C^2=ce−vfVt^+C1(T)⋅vfV⋅t^e−vfVt^{{\hat{C}}_{2}}=c{{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}}+{{C}_{1}}\left( T \right)\cdot \frac{{{v}_{f}}}{V}\cdot \hat{t}{{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}}C^2=ce−Vvft^+C1(T)⋅Vvf⋅t^e−Vvft^
将初值代入式(2.3)得c=C2(T)c={{C}_{2}}\left( T \right)c=C2(T)
得C^2=C2(T)e−vfVt^+C1(T)⋅vfV⋅te−vfVt^{{\hat{C}}_{2}}={{C}_{2}}\left( T \right){{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}}+{{C}_{1}}\left( T \right)\cdot \frac{{{v}_{f}}}{V}\cdot t{{e}^{-\frac{{{v}_{f}}}{V}\hat{t}}}C^2=C2(T)e−Vvft^+C1(T)⋅Vvf⋅te−Vvft^
7.2.3 反应池3
工作了太大,不算了
7.3 传递函数解法
使用传递函数和simulink仿真。三个反应池都是一样的,因此只需要解出一个池子即可。
列出微分方程dCOdt+vfVCO=vfVCI\frac{d{{C}_{O}}}{dt}+\frac{{{v}_{f}}}{V}{{C}_{O}}=\frac{{{v}_{f}}}{V}{{C}_{I}}dtdCO+VvfCO=VvfCI
等式两边做拉普拉斯变换得出
sFCO(s)−Co(0)+vfVFCO(s)=vfVFCI(s)s{{F}_{CO}}\left( s \right)-{{C}_{o}}(0)+\frac{{{v}_{f}}}{V}{{F}_{CO}}\left( s \right)=\frac{{{v}_{f}}}{V}{{F}_{CI}}\left( s \right)sFCO(s)−Co(0)+VvfFCO(s)=VvfFCI(s)
令CO(0)=0{{C}_{O}}\left( 0 \right)=0CO(0)=0,可求得传递函数
H(s)=FCO(s)FCI(s)=vfVs+vfVH\left( s \right)=\frac{{{F}_{CO}}\left( s \right)}{{{F}_{CI}}\left( s \right)}=\frac{\frac{{{v}_{f}}}{V}}{s+\frac{{{v}_{f}}}{V}}H(s)=FCI(s)FCO(s)=s+VvfVvf
下图是simulink仿真结果。

7.4 数值计算和验证
7.4.1 反应池1
v_f=1; %流体流速,mL/s
V=0.008;%反应池体积,mL
C_01=20;%葡萄糖溶液瓶浓度
V_s=0.05;%液路中的葡萄糖体积
T=V_s/v_f; %单位 s
t_step=0.0001;
t11=0:t_step:T;
C11=(-1*exp((-v_f/V).*t11)+1)*C_01;
C11_T=C11(end);
t12=T+t_step:t_step:0.1;
C12=C11_T*exp((-v_f/V).*(t12-T));
t1 = [t11,t12];
C1 = [C11,C12];
figure();
hold on;
grid on;
plot(t1,C1);
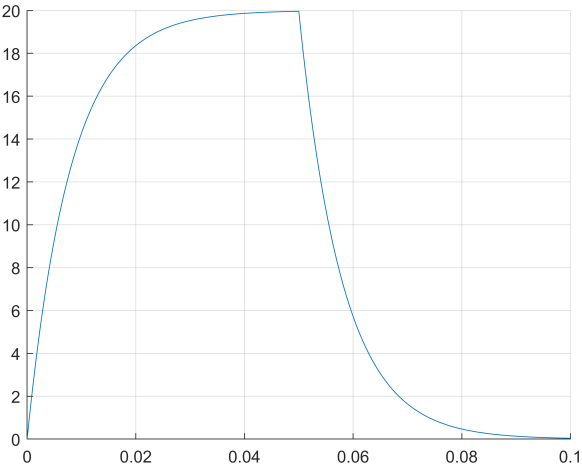
7.4.2 反应池2
C21=((-1-v_f/V.*t11).*exp((-v_f/V).*t11)+1)*C_01;
C21_T=C21(end);
C22=(C21_T+C11_T*(v_f/V).*(t12-T)).*exp((-v_f/V).*(t12-T));
C2 = [C21,C22];
figure();
hold on;
grid on;
plot(t1,C2);

7.4.3 反应池3
C31=((-1-v_f/V.*t11-0.5*(v_f/V.*t11).^2).*exp((-v_f/V).*t11)+1)*C_01;
C31_T=C31(end);
C32=(C31_T+C21_T*(v_f/V).*(t12-T)+0.5*C11_T.*(v_f/V.*(t12-T)).^2).*exp((-v_f/V).*(t12-T));
C3 = [C31,C32];
figure();
hold on;
grid on;
plot(t1,C3);

7.4.4 综合结果
figure();
hold on;
grid on;
plot(t1,C1);
plot(t1,C2);
plot(t1,C3);
legend('C1','C2','C3');
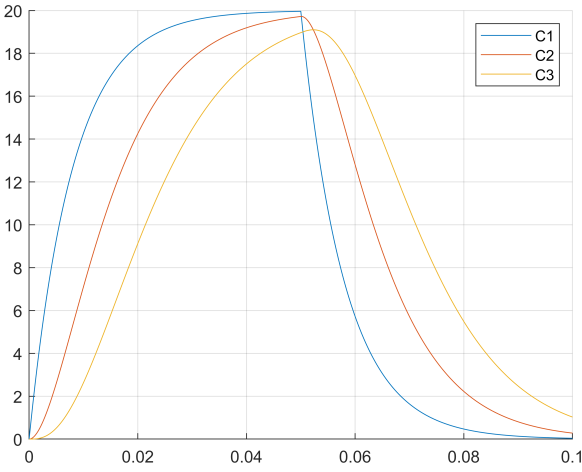
7.4.5 数值求解——反应池1
dt = t_step;
CC1=zeros( 1,length(C11)+length(C12) );
for i=2:1:length(C11)
CC1(i)=(CC1(i-1)*V - CC1(i-1)*dt*v_f + C_01*dt*v_f)/V;
end
for i=length(C11)+1:1:length(CC1)
CC1(i)=(CC1(i-1)*V - CC1(i-1)*dt*v_f)/V;
end
7.4.6 数值求解——反应池2
CC2=zeros( 1,length(CC1) );
for i=2:1:length(CC2)
CC2(i)=(CC2(i-1)*V - CC2(i-1)*dt*v_f + CC1(i-1)*dt*v_f)/V;
end
7.4.7 数值求解——反应池3
CC3=zeros( 1,length(CC1) );
for i=2:1:length(CC3)
CC3(i)=(CC3(i-1)*V - CC3(i-1)*dt*v_f + CC2(i-1)*dt*v_f)/V;
end
7.4.8 结果比较
figure();
hold on;
grid on;
plot(t1,C1);
plot(t1,C2);
plot(t1,C3);
plot(t1,CC1,':');
plot(t1,CC2,':');
plot(t1,CC3,':');
legend('C1','C2','C3','C1','C2','C3');
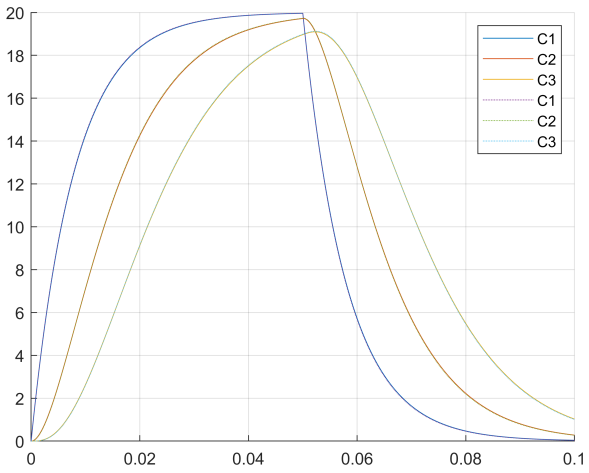




















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








