漫谈弹簧阻尼模型（上）

原创已于 2025-08-16 08:31:45 修改 · 1.2k 阅读

31 ·

CC 4.0 BY-SA版权

文章标签：

#算法

于 2025-05-04 22:33:19 首次发布

一前言

工程师常常需要为纷繁而复杂的工程问题寻找一个个简单的数学模型，弹簧阻尼模型算是我脑海中的常客，它曾经帮助我回答了一个汽车零件共振峰估计问题，最近的一个窄带信号频率估计的题目，也需要它和我一起完成答卷。我的智商有限，没见过世面，在此仅将一些破碎的想法拾掇拾掇，记录下来，就像小朋友整理卡通玩具一样。
一般的，人们会用如下一个非齐次二阶常微分来对模型进行抽象。
$md2xdt2+αdxdt+kx=F(t)(1.1)m\frac{{{d}^{2}}x}{d{{t}^{2}}}+\alpha \frac{dx}{dt}+kx=F(t)\tag{1.1}$
式中， $m$ 是滑块质量， $α\alpha$ 是阻尼系数， $k$ 是弹簧刚度系数， $x$ 是滑块偏移平衡位置的距离， $F (t)$ 是施迫函数（forcing function），就是工程师理解的外力。
式(1.1)复杂了点，二阶方程居然有 $m$ 、 $α\alpha$ 、 $k$ 三个系数，我的智商跟不上，需要稍微简化一点。两边同时除 $m$ ，得
$d2xdt2+αmdxdt+kmx=1mF(t)\frac{{{d}^{2}}x}{d{{t}^{2}}}+\frac{\alpha }{m}\frac{dx}{dt}+\frac{k}{m}x=\frac{1}{m}F(t)$
即
$d2xdt2+a1dxdt+a2x=F~(t)(1.2)\frac{{{d}^{2}}x}{d{{t}^{2}}}+{{a}_{1}}\frac{dx}{dt}+{{a}_{2}}x=\tilde{F}(t)\tag{1.2}$
尽管如此，但我还是先以式(1.1)来展开讨论，该式物理意义明确。

二求解共振频率

显然的，该模型描述的是受迫运动，工程师的关注点在于，共振频率在哪里，因为这是一个系统出事情的地方。方法应该是多种多样的，我以我熟悉的方式来解一下。
我们不妨设想一下，当 $F (t)$ 是白噪声，或者是冲激函数时， $x$ 将会有怎样的运动轨迹呢。这个问题等效于下图的描述
图1.1
在这里插入图片描述
于是，问题便转到对模型传递函数的讨论。

2.1 代数法

对式(1.1)两边求拉氏变换，写出传递函数
$H(s)=1ms2+αs+k(2.1)\text{H}(s)=\frac{1}{m{{s}^{2}}+\alpha s+k}\tag{2.1}$
现实世界仅在虚数轴上受到影响，不妨将 $s=jω\text{s=j}\omega$ 带入上式
$H(jω)=1−mω2+jαω+k(2.2)\text{H}(j\omega )=\frac{1}{-m{{\omega }^{2}}+j\alpha \omega +k}\tag{2.2}$
$∣H(jω)∣2=1∣−mω2+jαω+k∣2(2.3){{\left| \text{H}(j\omega ) \right|}^{2}}=\frac{1}{{{\left| -m{{\omega }^{2}}+j\alpha \omega +k \right|}^{2}}}\tag{2.3}$
$∣H(jω)∣2=1(k−mω2)2+α2ω2(2.4){{\left| \text{H}(j\omega ) \right|}^{2}}=\frac{1}{{{\left( k-m{{\omega }^{2}} \right)}^{2}}+{{\alpha }^{2}}{{\omega }^{2}}}\tag{2.4}$
当分母取最小值，解出的 $ω\omega$ 即共振频率。令 $B(ω)=(k−mω2)2+α2ω2\begin{matrix}\text{B}(\omega ) \end{matrix}={{\left( k-m{{\omega }^{2}} \right)}^{2}}+{{\alpha }^{2}}{{\omega }^{2}}$
展开可得
$B(ω)=m2ω4+α2ω2−2kmω2+k2\begin{matrix}\text{B}(\omega ) \end{matrix}={{m}^{2}}{{\omega }^{4}}+{{\alpha }^{2}}{{\omega }^{2}}-2km{{\omega }^{2}}+{{k}^{2}}$
对 $ω\omega$ 求导，可得
$dBdω=4m2ω3+2α2ω−4kmω\begin{matrix}\frac{dB}{d\omega }\end{matrix}=4{{m}^{2}}{{\omega }^{3}}+2{{\alpha }^{2}}\omega -4km\omega$
令 $dBdω=0\begin{matrix}\frac{dB}{d\omega }\end{matrix}=0$ ，解出
$ω2=2km−α22m2(2.5){{\omega }^{2}}=\frac{2km-{{\alpha }^{2}}}{2{{m}^{2}}}\tag{2.5}$
即
$ω=ωr=km−α22m2(2.6)\omega ={{\omega }_{r}}=\sqrt{\frac{k}{m}-\frac{{{\alpha }^{2}}}{2{{m}^{2}}}}\tag{2.6}$
可以交作业了。
但是，我终究不是个聪明人，不喜欢把公式摆弄来摆弄去，总想着寻找一种几何作图的方法，就像小朋友画画一样。

2.2 几何法

由式(2.1)启发出几何方法是自然的，如果学过复分析的话（在后面的叙述中，读者也不难发现这点）。
令 $H(s)\text{H}(s)$ 分母为0，求出极点。
$ms2+αs+k=0m{{s}^{2}}+\alpha s+k=0$
如果系统是共振的，或者说欠阻尼的，就要求
$α2−4mk<0{{\alpha }^{2}}-4mk<0$
求出极点
$s12=−α±j4mk−α22m(2.7){{s}_{12}}=\frac{-\alpha \pm j\sqrt{4mk-{{\alpha }^{2}}}}{2m}\tag{2.7}$
另外，对临界阻尼系统，极点是 $s12=−α2m{{s}_{12}}=-\frac{\alpha }{2m}$ ，过阻尼系统的极点则是 $s12=−α±α2−4mk2m{{s}_{12}}=\frac{-\alpha \pm \sqrt{{{\alpha }^{2}}-4mk}}{2m}$ 。画出欠阻尼系统的极点图，并且在虚数轴上取值为 $ω\omega$ ，两个极点到 $ω\omega$ 的距离分别为 ${{r}_{1}}$ 、 ${{r}_{2}}$ 。
图1.2
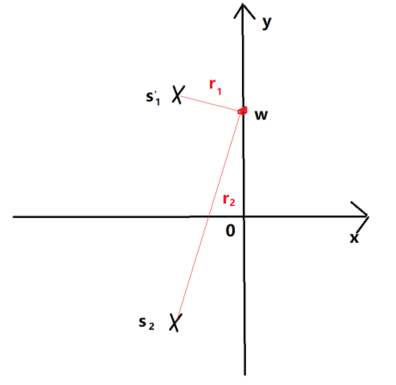
在这里插入图片描述
令 $a=α2m(2.8)a=\frac{\alpha }{2m}\tag{2.8}$ ， $b=4mk−α22m(2.9)b=\frac{\sqrt{4mk-{{\alpha }^{2}}}}{2m}\tag{2.9}$ ，可得到
图1.3

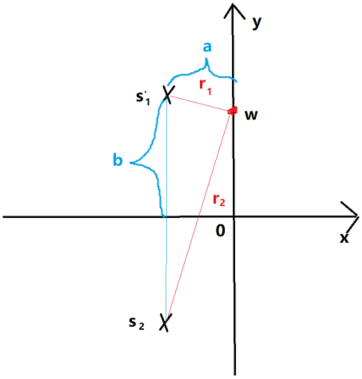
当 $1r11r2\frac{1}{{{r}_{1}}}\frac{1}{{{r}_{2}}}$ 取最大值时，即 ${{r}_{1}}{{r}_{2}}$ 取最大值时的 $ω\omega$ 就是共振频率点 $ωr{\omega }_{r}$
让我们看图写作。
${r12=a2+(b−ω)2r22=a2+(b+ω)2\left\{ \begin{matrix} {{r}_{1}}^{2}={{a}^{2}}+{{\left( b-\omega \right)}^{2}} \\ {{r}_{2}}^{2}={{a}^{2}}+{{\left( b+\omega \right)}^{2}} \\ \end{matrix} \right.$
可得
$r12r22=(a2+(b−ω)2)(a2+(b+ω)2){{r}_{1}}^{2}{{r}_{2}}^{2}=\left( {{a}^{2}}+{{\left( b-\omega \right)}^{2}} \right)\left( {{a}^{2}}+{{\left( b+\omega \right)}^{2}} \right)$
展开
$r12r22=a4+2a2b2+2a2ω2+b4−2b2ω2+ω4{{r}_{1}}^{2}{{r}_{2}}^{2}={{a}^{4}}+2{{a}^{2}}{{b}^{2}}+2{{a}^{2}}{{\omega }^{2}}+{{b}^{4}}-2{{b}^{2}}{{\omega }^{2}}+{{\omega }^{4}}$
令 $W={{r}_{1}}^{2}{{r}_{2}}^{2}$ ，并且对 $ω\omega$ 求导可得
$dWdω=4ω3+4a2ω−4b2ω\frac{dW}{d\omega }=4{{\omega }^{3}}+4{{a}^{2}}\omega -4{{b}^{2}}\omega$
令
$dWdω=0\frac{dW}{d\omega }=0$
得
$ω2=b2−a2{{\omega }^{2}}={{b}^{2}}-{{a}^{2}}$
将 $a=α2ma=\frac{\alpha }{2m}$ ， $b=4mk−α22mb=\frac{\sqrt{4mk-{{\alpha }^{2}}}}{2m}$ 代入上式即可求出 $ωr{{\omega }_{r}}$ 。
可以重新提交作业了。

三 AR谱估计

故事还没有结束。我们回头看一眼式(1.2)，这是微分方程，我这类的工程师经常和差分方程打交道，微分方程和差分方程，在我看来是没有什么区别的（一个是不可数无穷维向量，一个是可数无穷维向量，当后者的间隔 $△t\vartriangle t$ 趋于无穷小，差分便转化成了微分）。即我们可以进一步思考，这是个数字化系统的话，又该如何求解。
式(1.2)经过数字化，我们就得到了一个AR2模型。
$ω[t]+a1ω[t−1]+a2ω[t−2]=e[t](3.1)\omega \left[ t \right]+{{a}_{1}}\omega \left[ t-1 \right]+{{a}_{2}}\omega \left[ t-2 \right]=e\left[ t \right]\tag{3.1}$
让我们仿照连续模型，拿起A4纸和笔写写画画吧。

3.1 代数法

对式(3.1)左右两端做拉氏变换，列出传递函数
$G=11+a1Z−1+a2Z−2(3.2)G=\frac{1}{1+{{a}_{1}}{{Z}^{-1}}+{{a}_{2}}{{Z}^{-2}}}\tag{3.2}$
单位圆上使得 $∣G∣\left| G \right|$ 最大的 $ω\omega$ 就是 $ωr{{\omega }_{r}}$ 。
将 ${{Z}^{-1}}={{e}^{iw}}$ 带入式(3.2)，得
$G=11+a1eiw+a2ei2wG=\frac{1}{1+{{a}_{1}}{{e}^{iw}}+{{a}_{2}}{{e}^{i2w}}}$
用欧拉公式展开，得
$G=11+a1cos⁡ω+ia1sin⁡ω+a2cos⁡2ω+ia2sin⁡2ωG=\frac{1}{1+{{a}_{1}}\cos \omega +i{{a}_{1}}\sin \omega +{{a}_{2}}\cos 2\omega +i{{a}_{2}}\sin 2\omega }$
$G=1(1+a1cos⁡ω+a2cos⁡2ω)+i(a1sin⁡ω+a2sin⁡2ω)G=\frac{1}{\left( 1+{{a}_{1}}\cos \omega +{{a}_{2}}\cos 2\omega \right)+i\left( {{a}_{1}}\sin \omega +{{a}_{2}}\sin 2\omega \right)}$
模长
$∣G∣=1∣(1+a1cos⁡ω+a2cos⁡2ω)+i(a1sin⁡ω+a2sin⁡2ω)∣\left| G \right|=\frac{1}{\left| \left( 1+{{a}_{1}}\cos \omega +{{a}_{2}}\cos 2\omega \right)+i\left( {{a}_{1}}\sin \omega +{{a}_{2}}\sin 2\omega \right) \right|}$
$∣G∣=1(1+a1cos⁡ω+a2cos⁡2ω)2+(a1sin⁡ω+a2sin⁡2ω)2\left| G \right|=\frac{1}{\sqrt{{{\left( 1+{{a}_{1}}\cos \omega +{{a}_{2}}\cos 2\omega \right)}^{2}}+{{\left( {{a}_{1}}\sin \omega +{{a}_{2}}\sin 2\omega \right)}^{2}}}}$
当分母最小时， $∣G∣\left| G \right|$ 最大。令
$B=(1+a1cos⁡ω+a2cos⁡2ω)2+(a1sin⁡ω+a2sin⁡2ω)2B={{\left( 1+{{a}_{1}}\cos \omega +{{a}_{2}}\cos 2\omega \right)}^{2}}+{{\left( {{a}_{1}}\sin \omega +{{a}_{2}}\sin 2\omega \right)}^{2}}$
展开整理得
$B=(1+a1cos⁡ω+a2cos⁡2ω)(1+a1cos⁡ω+a2cos⁡2ω)+(a1sin⁡ω+a2sin⁡2ω)(a1sin⁡ω+a2sin⁡2ω)B=\left( 1+{{a}_{1}}\cos \omega +{{a}_{2}}\cos 2\omega \right)\left( 1+{{a}_{1}}\cos \omega +{{a}_{2}}\cos 2\omega \right)+\left( {{a}_{1}}\sin \omega +{{a}_{2}}\sin 2\omega \right)\left( {{a}_{1}}\sin \omega +{{a}_{2}}\sin 2\omega \right)$
$B=1+a1cos⁡ω+a2cos⁡2ω+a1cos⁡ω+a12cos⁡2ω+a1a2cos⁡ωcos⁡2ω+a2cos⁡2ω.+a1a2cos⁡ωcos⁡2ω+a22cos⁡22ω+a12sin⁡2ω+a22sin⁡22ω+2a1sin⁡ωa2sin⁡2ωB=1+{{a}_{1}}\cos \omega +{{a}_{2}}\cos 2\omega +{{a}_{1}}\cos \omega +{{a}_{1}}^{2}{{\cos }^{2}}\omega +{{a}_{1}}{{a}_{2}}\cos \omega \cos 2\omega +{{a}_{2}}\cos 2\omega .+{{a}_{1}}{{a}_{2}}\cos \omega \cos 2\omega +{{a}_{2}}^{2}{{\cos }^{2}}2\omega +{{a}_{1}}^{2}{{\sin }^{2}}\omega +{{a}_{2}}^{2}{{\sin }^{2}}2\omega +2{{a}_{1}}\sin \omega {{a}_{2}}\sin 2\omega$
$B=1+2a1cos⁡ω+2a2cos⁡2ω+a12cos⁡2ω+2a1a2cos⁡ωcos⁡2ω+a22cos⁡22ω+a12sin⁡2ω+a22sin⁡22ω+2a1sin⁡ωa2sin⁡2ωB=1+2{{a}_{1}}\cos \omega +2{{a}_{2}}\cos 2\omega +{{a}_{1}}^{2}{{\cos }^{2}}\omega +2{{a}_{1}}{{a}_{2}}\cos \omega \cos 2\omega +{{a}_{2}}^{2}{{\cos }^{2}}2\omega +{{a}_{1}}^{2}{{\sin }^{2}}\omega +{{a}_{2}}^{2}{{\sin }^{2}}2\omega +2{{a}_{1}}\sin \omega {{a}_{2}}\sin 2\omega$
$B=1+2a1cos⁡ω+2a2cos⁡2ω+a12+2a1a2cos⁡ωcos⁡2ω+a22+2a1a2sin⁡ωsin⁡2ωB=1+2{{a}_{1}}\cos \omega +2{{a}_{2}}\cos 2\omega +{{a}_{1}}^{2}+2{{a}_{1}}{{a}_{2}}\cos \omega \cos 2\omega +{{a}_{2}}^{2}+2{{a}_{1}}{{a}_{2}}\sin \omega \sin 2\omega$
令 $dBdω=0\frac{dB}{d\omega }=0$ ，可得
$−2a1sin⁡ω−4a2sin⁡2ω−2a1a2sin⁡ωcos⁡2ω−4a1a2cos⁡ωsin⁡2ω+2a1a2cos⁡ωsin⁡2ω+4a1a2sin⁡ωcos⁡2ω=0-2{{a}_{1}}\sin \omega -4{{a}_{2}}\sin 2\omega -2{{a}_{1}}{{a}_{2}}\sin \omega \cos 2\omega -4{{a}_{1}}{{a}_{2}}\cos \omega \sin 2\omega +2{{a}_{1}}{{a}_{2}}\cos \omega \sin 2\omega +4{{a}_{1}}{{a}_{2}}\sin \omega \cos 2\omega =0$
$−a1sin⁡ω−2a2sin⁡2ω−a1a2sin⁡ωcos⁡2ω−2a1a2cos⁡ωsin⁡2ω+a1a2cos⁡ωsin⁡2ω+2a1a2sin⁡ωcos⁡2ω=0-{{a}_{1}}\sin \omega -2{{a}_{2}}\sin 2\omega -{{a}_{1}}{{a}_{2}}\sin \omega \cos 2\omega -2{{a}_{1}}{{a}_{2}}\cos \omega \sin 2\omega +{{a}_{1}}{{a}_{2}}\cos \omega \sin 2\omega +2{{a}_{1}}{{a}_{2}}\sin \omega \cos 2\omega =0$
$−a1sin⁡ω−2a2sin⁡2ω+a1a2sin⁡ωcos⁡2ω−a1a2cos⁡ωsin⁡2ω=0-{{a}_{1}}\sin \omega -2{{a}_{2}}\sin 2\omega +{{a}_{1}}{{a}_{2}}\sin \omega \cos 2\omega -{{a}_{1}}{{a}_{2}}\cos \omega \sin 2\omega =0$
$−a1sin⁡ω−2a2sin⁡2ω+a1a212(sin⁡3ω−sin⁡ω)−a1a212(sin⁡3ω+sin⁡ω)=0-{{a}_{1}}\sin \omega -2{{a}_{2}}\sin 2\omega +{{a}_{1}}{{a}_{2}}\frac{1}{2}(\sin 3\omega -\sin \omega )-{{a}_{1}}{{a}_{2}}\frac{1}{2}(\sin 3\omega +\sin \omega )=0$
$−a1sin⁡ω−2a2sin⁡2ω+(12a1a2sin⁡3ω−12a1a2sin⁡ω)−(12a1a2sin⁡3ω+12a1a2sin⁡ω)=0-{{a}_{1}}\sin \omega -2{{a}_{2}}\sin 2\omega +(\frac{1}{2}{{a}_{1}}{{a}_{2}}\sin 3\omega -\frac{1}{2}{{a}_{1}}{{a}_{2}}\sin \omega )-(\frac{1}{2}{{a}_{1}}{{a}_{2}}\sin 3\omega +\frac{1}{2}{{a}_{1}}{{a}_{2}}\sin \omega )=0$
$−a1sin⁡ω−2a2sin⁡2ω−a1a2sin⁡ω=0-{{a}_{1}}\sin \omega -2{{a}_{2}}\sin 2\omega -{{a}_{1}}{{a}_{2}}\sin \omega =0$
$−a1sin⁡ω−4a2sin⁡ωcos⁡ω−a1a2sin⁡ω=0-{{a}_{1}}\sin \omega -4{{a}_{2}}\sin \omega \cos \omega -{{a}_{1}}{{a}_{2}}\sin \omega =0$
$−4a2cos⁡ω=(a1a2+a1)-4{{a}_{2}}\cos \omega =({{a}_{1}}{{a}_{2}}+{{a}_{1}})$
$cos⁡ω=−(a1a2+a1)4a2\cos \omega =-\frac{({{a}_{1}}{{a}_{2}}+{{a}_{1}})}{4{{a}_{2}}}$
好，作业完成。
如果知道采样时间 ${{T}_{s}}$ ，那么可以求出以Hz为单位的频率
$fr=12πTsarccos⁡(−(a1a2+a1)4a2)(3.3){{\text{f}}_{\text{r}}}=\frac{1}{2\pi {{T}_{s}}}\arccos (-\frac{({{a}_{1}}{{a}_{2}}+{{a}_{1}})}{4{{a}_{2}}})\tag{3.3}$

3.2 几何法

由式(3.2)得
$G=Z2Z2+a1Z1+a2(3.4)G=\frac{{{Z}^{2}}}{{{Z}^{2}}+{{a}_{1}}{{Z}^{1}}+{{a}_{2}}}\tag{3.4}$
可知两个零点在原点，对频率响应的幅度没有影响，可以不用考虑。求极点需要令分母等于0，即
${{Z}^{2}}+{{a}_{1}}{{Z}^{1}}+{{a}_{2}}=0$
求得极点是
$Z12=−a1±a12−4a22(3.5){{Z}_{12}}=\frac{-{{a}_{1}}\pm \sqrt{{{a}_{1}}^{2}-4{{a}_{2}}}}{2}\tag{3.5}$
如果模型能够求出共振频率，要求 $Z$ 的解存在共轭复数，即要求 ${{a}_{1}}^{2}-4{{a}_{2}}<0$ 。因此
$Z12=−a1±i4a2−a122{{Z}_{12}}=\frac{-{{a}_{1}}\pm i\sqrt{4{{a}_{2}}-{{a}_{1}}^{2}}}{2}$
写成实部和虚部的形式
$Z12=−a12±i4a2−a122(3.6){{Z}_{12}}=\frac{-{{a}_{1}}}{2}\pm \frac{i\sqrt{4{{a}_{2}}-{{a}_{1}}^{2}}}{2}\tag{3.6}$
再写成极坐标形式
$Z=reiw(3.7)Z=r{{e}^{iw}}\tag{3.7}$
联立式(3.6、式(3.7)解得极点角频率
$ω0=arccos⁡−a12a2(3.8){{\omega }_{\text{0}}}=\arccos \frac{-{{a}_{1}}}{2\sqrt{{{a}_{2}}}}\tag{3.8}$
画出零极点图
在这里插入图片描述
使 $1r11r2\frac{1}{{{r}_{1}}}\frac{1}{{{r}_{2}}}$ 最大，即 ${{r}_{1}}{{r}_{2}}$ 最小，即 ${{r}_{1}}^{2}{{r}_{2}}^{2}$ 最小的 $ω\omega$ 就是 $ωr{{\omega }_{r}}$ 。接下来就是看图写作了。
${r12=c2+1−2ccos⁡(ω0−ω)r22=c2+1−2ccos⁡(ω0+ω)\left\{ \begin{matrix} {{r}_{1}}^{2}={{c}^{2}}+1-2c\cos ({{\omega }_{0}}-\omega ) \\ {{r}_{2}}^{2}={{c}^{2}}+1-2c\cos ({{\omega }_{0}}+\omega ) \\ \end{matrix} \right.$
$r12r22=(c2+1−2ccos⁡(ω0−ω))(c2+1−2ccos⁡(ω0+ω)){{r}_{1}}^{2}{{r}_{2}}^{2}=\left( {{c}^{2}}+1-2c\cos ({{\omega }_{0}}-\omega ) \right)\left( {{c}^{2}}+1-2c\cos ({{\omega }_{0}}+\omega ) \right)$
$r12r22=((c2+1)−2ccos⁡(ω0−ω))((c2+1)−2ccos⁡(ω0+ω)){{r}_{1}}^{2}{{r}_{2}}^{2}=\left( \left( {{c}^{2}}+1 \right)-2c\cos ({{\omega }_{0}}-\omega ) \right)\left( \left( {{c}^{2}}+1 \right)-2c\cos ({{\omega }_{0}}+\omega ) \right)$
$r12r22=((c2+1)−2ccos⁡ω0cos⁡ω−2csin⁡ω0sin⁡ω)((c2+1)−2ccos⁡ω0cos⁡ω+2csin⁡ω0sin⁡ω){{r}_{1}}^{2}{{r}_{2}}^{2}=\left( \left( {{c}^{2}}+1 \right)-2c\cos {{\omega }_{0}}\cos \omega -2c\sin {{\omega }_{0}}\sin \omega \right)\left( \left( {{c}^{2}}+1 \right)-2c\cos {{\omega }_{0}}\cos \omega +2c\sin {{\omega }_{0}}\sin \omega \right)$
$r12r22=(c2+1)2−2c(c2+1)cos⁡ω0cos⁡ω+2c(c2+1)sin⁡ω0sin⁡ω−2c(c2+1)cos⁡ω0cos⁡ω+4c2cos⁡2ω0cos⁡2ω−4c2cos⁡ω0cos⁡ωsin⁡ω0sin⁡ω−2c(c2+1)sin⁡ω0sin⁡ω+4c2cos⁡ω0cos⁡ωsin⁡ω0sin⁡ω−4c2sin⁡2ω0sin⁡2ω{{r}_{1}}^{2}{{r}_{2}}^{2}={{\left( {{c}^{2}}+1 \right)}^{2}}-2c\left( {{c}^{2}}+1 \right)\cos {{\omega }_{0}}\cos \omega +2c\left( {{c}^{2}}+1 \right)\sin {{\omega }_{0}}\sin \omega -2c\left( {{c}^{2}}+1 \right)\cos {{\omega }_{0}}\cos \omega +4{{c}^{2}}{{\cos }^{2}}{{\omega }_{0}}{{\cos }^{2}}\omega -4{{c}^{2}}\cos {{\omega }_{0}}\cos \omega \sin {{\omega }_{0}}\sin \omega -2c\left( {{c}^{2}}+1 \right)\sin {{\omega }_{0}}\sin \omega +4{{c}^{2}}\cos {{\omega }_{0}}\cos \omega \sin {{\omega }_{0}}\sin \omega -4{{c}^{2}}{{\sin }^{2}}{{\omega }_{0}}{{\sin }^{2}}\omega$
$r12r22=(c2+1)2−4c(c2+1)cos⁡ω0cos⁡ω+4c2cos⁡2ω0cos⁡2ω−4c2sin⁡2ω0sin⁡2ω{{r}_{1}}^{2}{{r}_{2}}^{2}={{\left( {{c}^{2}}+1 \right)}^{2}}-4c\left( {{c}^{2}}+1 \right)\cos {{\omega }_{0}}\cos \omega +4{{c}^{2}}{{\cos }^{2}}{{\omega }_{0}}{{\cos }^{2}}\omega -4{{c}^{2}}{{\sin }^{2}}{{\omega }_{0}}{{\sin }^{2}}\omega$
令 $d(r12r22)dω=0\frac{d({{r}_{1}}^{2}{{r}_{2}}^{2})}{d\omega }=0$
$4c(c2+1)cos⁡ω0sin⁡ω−8c2cos⁡2ω0sin⁡ωcos⁡ω−8c2sin⁡2ω0sin⁡ωcos⁡ω=04c\left( {{c}^{2}}+1 \right)\cos {{\omega }_{0}}\sin \omega -8{{c}^{2}}{{\cos }^{2}}{{\omega }_{0}}\sin \omega \cos \omega -8{{c}^{2}}{{\sin }^{2}}{{\omega }_{0}}\sin \omega \cos \omega =0$
$4c(c2+1)cos⁡ω0sin⁡ω−(8c2cos⁡2ω0+8c2sin⁡2ω0)sin⁡ωcos⁡ω=04c\left( {{c}^{2}}+1 \right)\cos {{\omega }_{0}}\sin \omega -(8{{c}^{2}}{{\cos }^{2}}{{\omega }_{0}}+8{{c}^{2}}{{\sin }^{2}}{{\omega }_{0}})\sin \omega \cos \omega =0$
$c(c2+1)cos⁡ω0sin⁡ω=2c2sin⁡ωcos⁡ωc\left( {{c}^{2}}+1 \right)\cos {{\omega }_{0}}\sin \omega =2{{c}^{2}}\sin \omega \cos \omega$
$cos⁡ω=(c2+1)cos⁡ω02c\cos \omega =\frac{\left( {{c}^{2}}+1 \right)\cos {{\omega }_{0}}}{2c}$
$cos⁡ω=−(a2+1)a14a2\cos \omega =-\left( {{a}_{2}}+1 \right)\frac{{{a}_{1}}}{4{{a}_{2}}}$

四最小二乘与参数辨识

假设存在这样一个问题，对于式(1.2)和式(3.1)，不知道 ${{a}_{1}}$ 、 ${{a}_{1}}$ 的情况下如何求出 $ωr{{\omega }_{r}}$ ，甚至进一步的，连 $F~(t)\tilde{F}(t)$ 或 $e[t]e\left[ t \right]$ 也无从得知，只知道他们的某些统计特性，比如，服从Gauss分布的白噪声。这个问题是具有非常现实的工程意义的。设想这样一个题目，一辆车在路上跑，领导让你求出汽车轮毂的 $ωr{{\omega }_{r}}$ ，给到你的资料仅有加速度传感器输出的振动信号。对于搞车振的工程师来说，这不是难题，求出功率谱密度曲线，找峰值就行了。让我们把题目加深一下，车子边跑着，小ECU实时地把 $ωr{{\omega }_{r}}$ 算出来，通过CAN BUS发出来。小小的ECU，要内存没内存，要速度没速度，这可怎么办？事实上，就算把PC机搬上来，由于不确定性原理的限制和汽车行驶的非平稳性，也没法做到实时。这样一道题目曾经真切地摆在我面前（在此之前，它和其他更加复杂的问题交织在一起，让两位名校博士交了白卷。也许工科生的数学水平堪忧吧，我大量地检索了相关论文，所有的文献无一幸免地都把极点频率当成了共振频率，而这只是一张A4纸就能算明白的事情）。
解题的关键就在于估计出 ${{a}_{1}}$ 、 ${{a}_{1}}$ ，这是一个经典的参数辨识问题。
最小二乘是解题的钥匙之一。

4.1 代数法

令
$θ=[a1a2]T(4.1)\mathbf{\theta }={{\left[ \begin{matrix} {{a}_{1}} & {{a}_{2}} \end{matrix} \right]}^{T}}\tag{4.1}$
$φ(t)=[−ω(t−1)−ω(t−2)]T(4.2)\mathbf{\varphi }(t)={{\left[ \begin{matrix} -\omega (t-1) & -\omega (t-2) \end{matrix} \right]}^{T}}\tag{4.2}$
式(3.1)可以写成
$ω(t)=φT(t)θ+e(t)(4.3)\omega (t)={{\mathbf{\varphi }}^{T}}(t)\mathbf{\theta }+e(t)\tag{4.3}$
当ECU采集到N组数据，可以列出N-2组式(4.3)，那么求解出 $θ\mathbf{\theta }$ 便是一件简单的事情了。将N-2组公式列出来。
${ω(3)=φT(3)θ+e(3)ω(4)=φT(4)θ+e(4)ω(5)=φT(5)θ+e(5)...ω(N)=φT(N)θ+e(N)\left\{ \begin{align} & \omega (3)={{\mathbf{\varphi }}^{T}}(3)\mathbf{\theta }+e(3) \\ & \omega (4)={{\mathbf{\varphi }}^{T}}(4)\mathbf{\theta }+e(4) \\ & \omega (5)={{\mathbf{\varphi }}^{T}}(5)\mathbf{\theta }+e(5) \\ & ... \\ & \omega (N)={{\mathbf{\varphi }}^{T}}(N)\mathbf{\theta }+e(N) \\ \end{align} \right.$
改成矩阵形式，令
$ω=[ω(3)ω(4)ω(5)...ω(N)]T\mathbf{\omega }={{\left[ \begin{matrix} \omega (3) & \omega (4) & \omega (5) & ... & \omega (N) \\ \end{matrix} \right]}^{T}}$
$ψ=[φT(3)φT(4)φT(5)...φT(N)]\mathbf{\psi }=\left[ \begin{matrix} {{\mathbf{\varphi }}^{T}}(3) \\ {{\mathbf{\varphi }}^{T}}(4) \\ {{\mathbf{\varphi }}^{T}}(5) \\ ... \\ {{\mathbf{\varphi }}^{T}}(N) \\ \end{matrix} \right]$
$e=[e(3)e(4)e(5)...e(N)]T\mathbf{e}={{\left[ \begin{matrix} e(3) & e(4) & e(5) & ... & e(N) \\ \end{matrix} \right]}^{T}}$
可得
$ω=ψθ+e(4.4)\mathbf{\omega }=\mathbf{\psi \theta }+\mathbf{e}\tag{4.4}$
构建目标函数
$J(θ)=∑t=3N(ω−φT(t)θ)2J(\mathbf{\theta })=\sum\limits_{t=3}^{N}{{{(\omega -{{\mathbf{\varphi }}^{T}}(t)\mathbf{\theta })}^{2}}}$
为使 $J(θ)J(\mathbf{\theta })$ 最小，可以令
$∂J∂θ=0\frac{\partial J}{\partial \mathbf{\theta }}=0$
$∂∂θ[∑t=3N(ω−φT(t)θ)2]=0\frac{\partial }{\partial \mathbf{\theta }}\left[ \sum\limits_{t=3}^{N}{{{(\omega -{{\mathbf{\varphi }}^{T}}(t)\mathbf{\theta })}^{2}}} \right]=0$
即
$∂∂θ[(ω−ψθ)T(ω−ψθ)]=0\frac{\partial }{\partial \mathbf{\theta }}\left[ {{(\mathbf{\omega }-\mathbf{\psi \theta })}^{T}}(\mathbf{\omega }-\mathbf{\psi \theta }) \right]=0$
可得
$θ=(ψTψ)−1ψTω(4.5)\mathbf{\theta }={{({{\mathbf{\psi }}^{T}}\mathbf{\psi })}^{-1}}{{\mathbf{\psi }}^{T}}\mathbf{\omega }\tag{4.5}$

4.2 几何法

上述最小二乘的代数法解题思路，是使用最广泛，愚笨如我，总是喜欢几何法。在我看来，最小二乘，就是在希尔伯特空间上的一个正交投影而已。
对于式(4.4)的求解，即寻找一个参数 $θ\mathbf{\theta }$ ，使得 $∣e∣=∣ω−ψθ∣\left| \mathbf{e} \right|=\left| \mathbf{\omega }-\mathbf{\psi \theta } \right|$ 最小。我们可以将 $ω{\omega}$ 看成Euclidean空间 $RN{{\text{R}}^{\text{N}}}$ 中的向量，同样的，把矩阵 $ψ\mathbf{\psi }$ 的两个列向量
$ψ1=[ω(1)ω(2)ω(3)...ω(N−2)]T{{\mathbf{\psi }}_{1}}={{\left[ \begin{matrix} \omega (1) & \omega (2) & \omega (3) & ... & \omega (N-2) \\ \end{matrix} \right]}^{T}}$
$ψ2=[ω(2)ω(3)ω(4)...ω(N−1)]T{{\mathbf{\psi }}_{2}}={{\left[ \begin{matrix} \omega (2) & \omega (3) & \omega (4) & ... & \omega (N-1) \\ \end{matrix} \right]}^{T}}$
也看成为 $RN{{\text{R}}^{\text{N}}}$ 中的向量，那么 $ψ1{{\mathbf{\psi }}_{1}}$ 和 $ψ2{{\mathbf{\psi }}_{2}}$ 就可以张成一个二维子空间 $U=span(ψ1,ψ1)∈RN\text{U=span}({{\mathbf{\psi }}_{1}},{{\mathbf{\psi }}_{1}})\in {{R}^{N}}$ 。问题就转变成了在 $U\text{U}$ 中寻找一个向量 $ψθ=a1ψ1+a2ψ2\mathbf{\psi \theta }={{a}_{1}}{{\mathbf{\psi }}_{1}}+{{a}_{2}}{{\mathbf{\psi }}_{2}}$ ，使得 $∣ω−ψθ∣\left| \mathbf{\omega }-\mathbf{\psi \theta } \right|$ 最小。显然的，这时候的 $ψθ\mathbf{\psi \theta }$ 是 $ω\mathbf{\omega }$ 在 $U\text{U}$ 上的投影， $ω−ψθ\mathbf{\omega }-\mathbf{\psi \theta }$ 和 $U\text{U}$ 正交。
即对于 $∀γ∈U\forall \mathbf{\gamma }\in \text{U}$ ，有内积 $γT(ω−ψθ)=0{{\mathbf{\gamma }}^{T}}\left( \mathbf{\omega }-\mathbf{\psi \theta } \right)=0$ ， $γ\mathbf{\gamma }$ 有现成的，即 $ψ1{{\mathbf{\psi }}_{1}}$ 和 $ψ2{{\mathbf{\psi }}_{2}}$ 。
${ψ1T(ω−ψθ)=0ψ2T(ω−ψθ)=0\left\{ \begin{matrix} \mathbf{\psi }_{1}^{T}\left( \mathbf{\omega }-\mathbf{\psi \theta } \right)=0 \\ \mathbf{\psi }_{2}^{T}\left( \mathbf{\omega }-\mathbf{\psi \theta } \right)=0 \\ \end{matrix} \right.$
合起来写就是
$ψT(ω−ψθ)=0{{\mathbf{\psi }}^{T}}\left( \mathbf{\omega }-\mathbf{\psi \theta } \right)=0$
$ψTω−ψTψθ=0{{\mathbf{\psi }}^{T}}\mathbf{\omega }-{{\mathbf{\psi }}^{T}}\mathbf{\psi \theta }=0$
$θ=(ψTψ)−1ψTω\mathbf{\theta }={{\left( {{\mathbf{\psi }}^{T}}\mathbf{\psi } \right)}^{-1}}{{\mathbf{\psi }}^{T}}\mathbf{\omega }$

4.3 递归最小二乘

当数据量比较大的时候，式（4.5）求解起来就比较耗时了，需要寻求一种递推的方式进行求解。在这种情形下， $θ\mathbf{\theta }$ 就可以看成是数据项 $n$ 的函数 $θN{{\mathbf{\theta }}_{\text{N}}}$ ，其中的推导过程是纯粹的游戏。
$θN=(ψNTψN)−1ψNTωN{{\mathbf{\theta }}_{\text{N}}}={{\left( {{\mathbf{\psi }}_{N}}^{\text{T}}{{\mathbf{\psi }}_{N}} \right)}^{-1}}{{\mathbf{\psi }}_{N}}^{\text{T}}{{\mathbf{\omega }}_{N}}$
$θN+1=([ψN−ω(N−1)−ω(N)]T[ψN−ω(N−1)−ω(N)])−1[ψNT−ω(N−1)−ω(N)][ωNω(N+1)](4.6){{\mathbf{\theta }}_{\text{N+1}}}={{\left( {{\left[ \begin{matrix} {{\mathbf{\psi }}_{N}} & \begin{matrix} -\omega \left( N-1 \right) \\ -\omega \left( N \right) \\ \end{matrix} \\ \end{matrix} \right]}^{\text{T}}}\left[ \begin{matrix} {{\mathbf{\psi }}_{N}} \\ \begin{matrix} -\omega \left( N-1 \right) & -\omega \left( N \right) \\ \end{matrix} \\ \end{matrix} \right] \right)}^{-1}}\left[ \begin{matrix} {{\mathbf{\psi }}_{N}}^{\text{T}} & \begin{matrix} -\omega \left( N-1 \right) \\ -\omega \left( N \right) \\ \end{matrix} \\ \end{matrix} \right]\left[ \begin{matrix} {{\mathbf{\omega }}_{N}} \\ \omega \left( N+1 \right) \\ \end{matrix} \right]\tag{4.6}$
$θN+1=(ψNTψN+φN+1φN+1T)−1(ψNTωN+φN+1ωN+1)(4.7){{\mathbf{\theta }}_{\text{N+1}}}={{\left( {{\mathbf{\psi }}_{N}}^{T}{{\mathbf{\psi }}_{N}}+{{\mathbf{\varphi }}_{\text{N+}1}}{{\mathbf{\varphi }}_{\text{N+}1}}^{T} \right)}^{-1}}\left( {{\mathbf{\psi }}_{N}}^{T}{{\mathbf{\omega }}_{N}}+{{\mathbf{\varphi }}_{\text{N+}1}}{{\omega }_{\text{N+}1}} \right)\tag{4.7}$
令 $RN=ψNTψN{{\mathbf{R}}_{N}}={{\mathbf{\psi }}_{N}}^{T}{{\mathbf{\psi }}_{N}}$ ， $z=ψNTωN\mathbf{z}={{\mathbf{\psi }}_{N}}^{T}{{\mathbf{\omega }}_{N}}$ ，那么
$θN=(RN)−1zN(4.8){{\mathbf{\theta }}_{\text{N}}}={{\left( {{\mathbf{R}}_{N}} \right)}^{-1}}{{\mathbf{z}}_{N}}\tag{4.8}$
$θN+1=(RN+1)−1zN+1(4.9){{\mathbf{\theta }}_{\text{N+1}}}={{\left( {{\mathbf{R}}_{N+1}} \right)}^{-1}}{{\mathbf{z}}_{N+1}}\tag{4.9}$
即
$θN+1=(RN+φN+1φN+1T)−1(zN+φN+1ωN+1)(4.10){{\mathbf{\theta }}_{\text{N+1}}}={{\left( {{\mathbf{R}}_{N}}+{{\mathbf{\varphi }}_{\text{N+}1}}{{\mathbf{\varphi }}_{\text{N+}1}}^{T} \right)}^{-1}}\left( {{\mathbf{z}}_{N}}+{{\mathbf{\varphi }}_{\text{N+}1}}{{\omega }_{\text{N+}1}} \right)\tag{4.10}$
还可以引入遗忘因子 $λ\lambda$ ，得
$θN+1=(λRN+φN+1φN+1T)−1(λzN+φN+1ωN+1)(4.11){{\mathbf{\theta }}_{\text{N+1}}}={{\left( \lambda {{\mathbf{R}}_{N}}+{{\mathbf{\varphi }}_{\text{N+}1}}{{\mathbf{\varphi }}_{\text{N+}1}}^{T} \right)}^{-1}}\left( \lambda {{\mathbf{z}}_{N}}+{{\mathbf{\varphi }}_{\text{N+}1}}{{\omega }_{\text{N+}1}} \right)\tag{4.11}$
$RN+1=λRN+φN+1φN+1T(4.12){{\mathbf{R}}_{N+1}}=\lambda {{\mathbf{R}}_{N}}+{{\mathbf{\varphi }}_{\text{N+}1}}{{\mathbf{\varphi }}_{\text{N+}1}}^{T}\tag{4.12}$
$zN+1=(λzN+φN+1ωN+1)(4.13){{\mathbf{z}}_{\text{N+1}}}=\left( \lambda {{\mathbf{z}}_{N}}+{{\mathbf{\varphi }}_{\text{N+}1}}{{\omega }_{\text{N+}1}} \right)\tag{4.13}$
对于本模型而已，到这一步就可以结束了。但是，对于高阶的AR方程，或者说多变量RLS，方程中的逆是比较耗时的（没具体算过，大家都这么说），需要进一步优化。
有这样一个定理，如果方阵 $A$ 能拆分成如下形式
$A={{B}^{-1}}+C{{D}^{-1}}{{C}^{T}}$
有
$A−1=B−BC(D+CTBC)−1CTB{{A}^{-1}}=B-BC{{\left( D+{{C}^{T}}BC \right)}^{-1}}{{C}^{T}}B$
据此，将式(4.13)改写成
$RN+1=((λRN)−1)−1+φN+11φN+1T{{\mathbf{R}}_{N+1}}={{\left( {{\left( \lambda {{\mathbf{R}}_{N}} \right)}^{-1}} \right)}^{-1}}+{{\mathbf{\varphi }}_{\text{N+}1}}1{{\mathbf{\varphi }}_{\text{N+}1}}^{T}$
可得
$RN+1−1=(λRN)−1−(λRN)−1φN+1(1+φN+1T(λRN)−1φN+1)−1φN+1T(λRN)−1(4.14){{\mathbf{R}}_{N+1}}^{-1}={{\left( \lambda {{\mathbf{R}}_{N}} \right)}^{-1}}-{{\left( \lambda {{\mathbf{R}}_{N}} \right)}^{-1}}{{\mathbf{\varphi }}_{\text{N+}1}}{{\left( 1+{{\mathbf{\varphi }}_{\text{N+}1}}^{T}{{\left( \lambda {{\mathbf{R}}_{N}} \right)}^{-1}}{{\mathbf{\varphi }}_{\text{N+}1}} \right)}^{-1}}{{\mathbf{\varphi }}_{\text{N+}1}}^{T}{{\left( \lambda {{\mathbf{R}}_{N}} \right)}^{-1}}\tag{4.14}$
$RN+1−1=1λ(RN−1−RN−1φN+1φN+1TRN−1λ+φN+1TRN−1φN+1)(4.15){{\mathbf{R}}_{N+1}}^{-1}=\frac{1}{\lambda }\left( {{\mathbf{R}}_{N}}^{-1}-\frac{{{\mathbf{R}}_{N}}^{-1}{{\mathbf{\varphi }}_{\text{N+}1}}{{\mathbf{\varphi }}_{\text{N+}1}}^{T}{{\mathbf{R}}_{N}}^{-1}}{\lambda +{{\mathbf{\varphi }}_{\text{N+}1}}^{T}{{\mathbf{R}}_{N}}^{-1}{{\mathbf{\varphi }}_{\text{N+}1}}} \right)\tag{4.15}$
令 $P=R−1\mathbf{P}={{\mathbf{R}}^{-1}}$ ，式(4.15)改写成
$PN+1=1λ(PN−PNφN+1φN+1TPNλ+φN+1TPNφN+1)(4.16){{\mathbf{P}}_{N+1}}=\frac{1}{\lambda }\left( {{\mathbf{P}}_{N}}-\frac{{{\mathbf{P}}_{N}}{{\mathbf{\varphi }}_{\text{N+}1}}{{\mathbf{\varphi }}_{\text{N+}1}}^{T}{{\mathbf{P}}_{N}}}{\lambda +{{\mathbf{\varphi }}_{\text{N+}1}}^{T}{{\mathbf{P}}_{N}}{{\mathbf{\varphi }}_{\text{N+}1}}} \right)\tag{4.16}$
式(4.9)就可以改写成
$θN+1=PN+1zN+1(4.17){{\mathbf{\theta }}_{\text{N+1}}}={{\mathbf{P}}_{N+1}}{{\mathbf{z}}_{N+1}}\tag{4.17}$
到此，似乎可以画上句号了，但是好事者要将游戏进一步玩下去。令
$K=PNφN+1λ+φN+1TPNφN+1\mathbf{K}=\frac{{{\mathbf{P}}_{N}}{{\mathbf{\varphi }}_{\text{N+}1}}}{\lambda +{{\mathbf{\varphi }}_{\text{N+}1}}^{T}{{\mathbf{P}}_{N}}{{\mathbf{\varphi }}_{\text{N+}1}}}$ ，并且发现 $K=PN+1φN+1\mathbf{K}={{\mathbf{P}}_{N+1}}{{\mathbf{\varphi }}_{\text{N+}1}}$ ，那么式(4.16)可以改写成
$PN+1=1λ(PN−KφN+1TPN)(4.19){{\mathbf{P}}_{N+1}}=\frac{1}{\lambda }\left( {{\mathbf{P}}_{N}}-\mathbf{K}{{\mathbf{\varphi }}_{\text{N+}1}}^{T}{{\mathbf{P}}_{N}} \right)\tag{4.19}$
式(4.17)可以展开成
$θN+1=λPN+1zN+PN+1φN+1ωN+1(4.19){{\mathbf{\theta }}_{\text{N+1}}}=\lambda {{\mathbf{P}}_{N+1}}{{\mathbf{z}}_{N}}+{{\mathbf{P}}_{N+1}}{{\mathbf{\varphi }}_{\text{N+}1}}{{\omega }_{\text{N+}1}}\tag{4.19}$
将式(4.16)代入式(4.17)，得
$θN+1=PNzN−kφN+1TPNzN+PN+1φN+1ωN+1(4.20){{\mathbf{\theta }}_{\text{N+1}}}={{\mathbf{P}}_{N}}{{\mathbf{z}}_{N}}-\mathbf{k}{{\mathbf{\varphi }}_{\text{N+}1}}^{T}{{\mathbf{P}}_{N}}{{\mathbf{z}}_{N}}+{{\mathbf{P}}_{N+1}}{{\mathbf{\varphi }}_{\text{N+}1}}{{\omega }_{\text{N+}1}}\tag{4.20}$
$θN+1=θN−kφN+1TθN+kωN+1(4.21){{\mathbf{\theta }}_{\text{N+1}}}={{\mathbf{\theta }}_{N}}-\mathbf{k}{{\mathbf{\varphi }}_{\text{N+}1}}^{T}{{\mathbf{\theta }}_{N}}+\mathbf{k}{{\omega }_{\text{N+}1}}\tag{4.21}$
$θN+1=θN+k(ωN+1−φN+1TθN)(4.21){{\mathbf{\theta }}_{\text{N+1}}}={{\mathbf{\theta }}_{N}}+\mathbf{k}\left( {{\omega }_{\text{N+}1}}-{{\mathbf{\varphi }}_{\text{N+}1}}^{T}{{\mathbf{\theta }}_{N}} \right)\tag{4.21}$
最终可得
${PN+1=1λ(PN−PNφN+1φN+1TPNλ+φN+1TPNφN+1)K=PN+1φN+1θN+1=θN+k(ωN+1−φN+1TθN)\left\{ \begin{matrix} {{\mathbf{P}}_{N+1}}=\frac{1}{\lambda }\left( {{\mathbf{P}}_{N}}-\frac{{{\mathbf{P}}_{N}}{{\mathbf{\varphi }}_{\text{N+}1}}{{\mathbf{\varphi }}_{\text{N+}1}}^{T}{{\mathbf{P}}_{N}}}{\lambda +{{\mathbf{\varphi }}_{\text{N+}1}}^{T}{{\mathbf{P}}_{N}}{{\mathbf{\varphi }}_{\text{N+}1}}} \right) \\ \mathbf{K}={{\mathbf{P}}_{N+1}}{{\mathbf{\varphi }}_{\text{N+}1}} \\ {{\mathbf{\theta }}_{\text{N+1}}}={{\mathbf{\theta }}_{N}}+\mathbf{k}\left( {{\omega }_{\text{N+}1}}-{{\mathbf{\varphi }}_{\text{N+}1}}^{T}{{\mathbf{\theta }}_{N}} \right) \\ \end{matrix} \right.$
第一次看到这个式子，是在一位貌似清华博士的matlab代码里，他出算法，我干移植。问一下公式含义，只收到认真学习XXX的无聊回复——够拽，即使他的产出可用莫名其妙来形容，但是，好拽！

五拉氏变换

式(3.1)所描述的是一个AR2模型，这是时间序列分析领域的术语，而在电子信息领域，则称之为IIR。它常常与拉氏变换交织在一起。
拉式变换，到底是什么意思，我以前不知道，现在依旧不知道。它的提出者，拉普拉斯先生，把它当成一个解微分方程的技巧（在那个年代，类似的技巧太多了），拉氏本人，一开始也不知道它的含义，直到傅里叶变换的提出，拉氏明白了，这是个复频率的问题。但我仍旧不明白，只是有些微不足道的看法，在这里念叨念叨。
拉氏变换，给出了描述一个系统的可视化的几何方法，其重点在于零极点的理解。
一般的传递函数，对分子分母做因式分解，可写作如下形式，面对这样的一个形式，学过复分析读者自然会想到，这是定义了一个复平面上的向量场，工科生所谓的频谱只是这个向量场在虚数轴上的一个切片。
$H\left( s \right)=K\frac{\prod\limits_{m=1}^{M}{\left( s-{{Z}_{m}} \right)}}{\prod\limits_{n=1}^{N}{\left( s-{{Z}_{n}} \right)}}$
让我们举例几个简单的例子。

5.1 极点

如图，是一个RC低通滤波器的幅频特性曲线和相频率特性曲线。
图5.1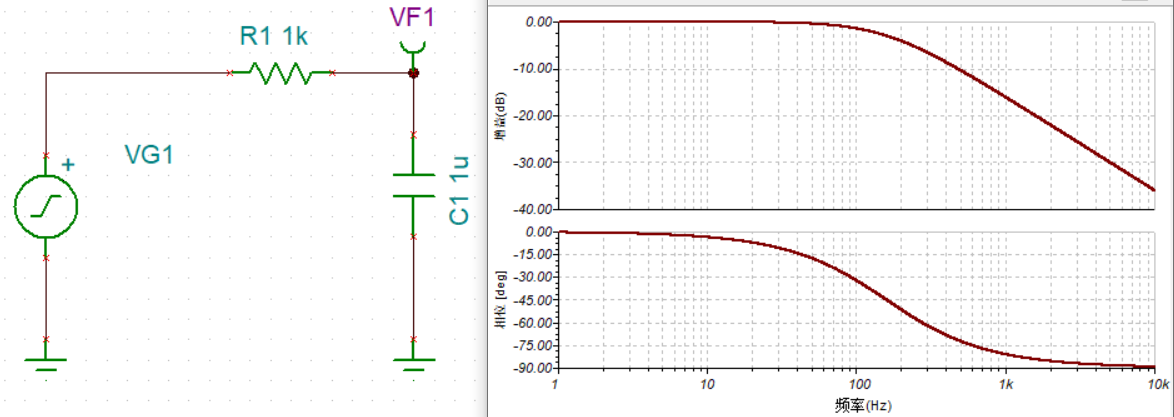 在这里插入图片描述
让我们到从二维平面向量场的角度来看看两条曲线是如何来的。写出传递函数
$H(s)=1RCs+1(5.1)\text{H}\left( \text{s} \right)=\frac{1}{\text{RCs+1}}\tag{5.1}$
即
$H(s)=1RC⋅1s+1RC\text{H}\left( \text{s} \right)=\frac{1}{RC}\centerdot \frac{1}{\text{s+}\frac{\text{1}}{RC}}$
$H(s)=k1s-s1(5.2)\text{H}\left( \text{s} \right)=k\frac{1}{\text{s-}{{\text{s}}_{\text{1}}}}\tag{5.2}$
存在一个极点 $s1=-1RC=−1000{{\text{s}}_{1}}\text{=-}\frac{\text{1}}{RC}=-1000$ ，看一下极点附近的场——请仔细看脚本，绘制的是波利亚向量场。

R = 1000;    %1K
C = 10^(-6); %1uF
Z1 = -1/(R*C) %极点
[X,Y] = meshgrid( -1100:10:-900 , -100:10:100 );
Z = X + 1i*Y;
H = 1./((R*C)*Z+1); %生成向量场 
H_db = 20*log10(abs(H)); %转为分贝值
m = abs(H)./H_db;        %
H_polya = conj(H)./m;    %修改为波利亚向量场
H_db_r = real(H_polya);  %取实部
H_db_i = imag(H_polya);  %取虚部

figure(); hold on;
quiver(X,Y,H_db_r,H_db_i);
grid on;

图5.2
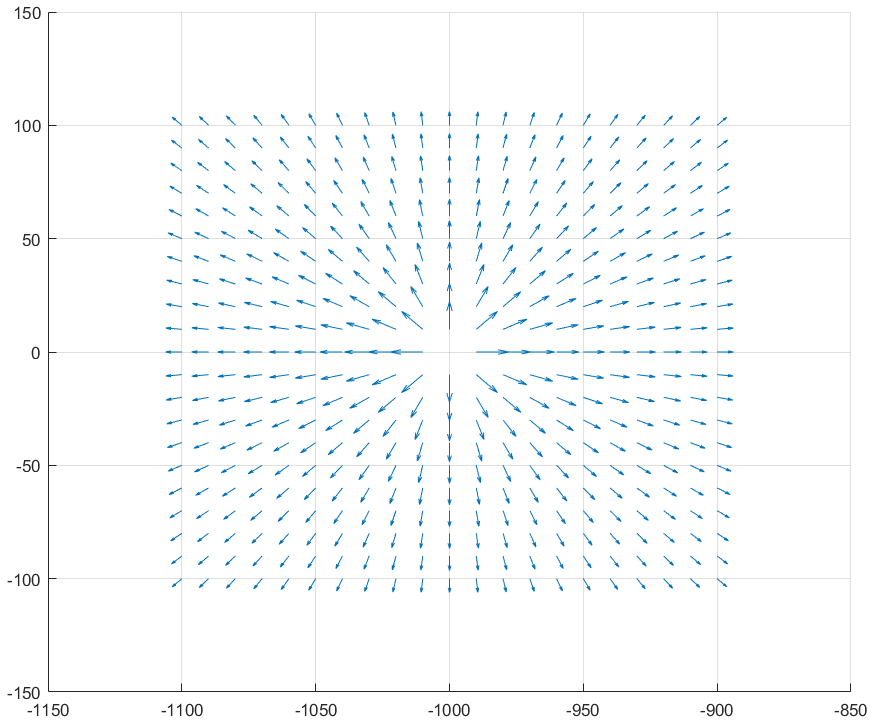
在这里插入图片描述
上个色看看。

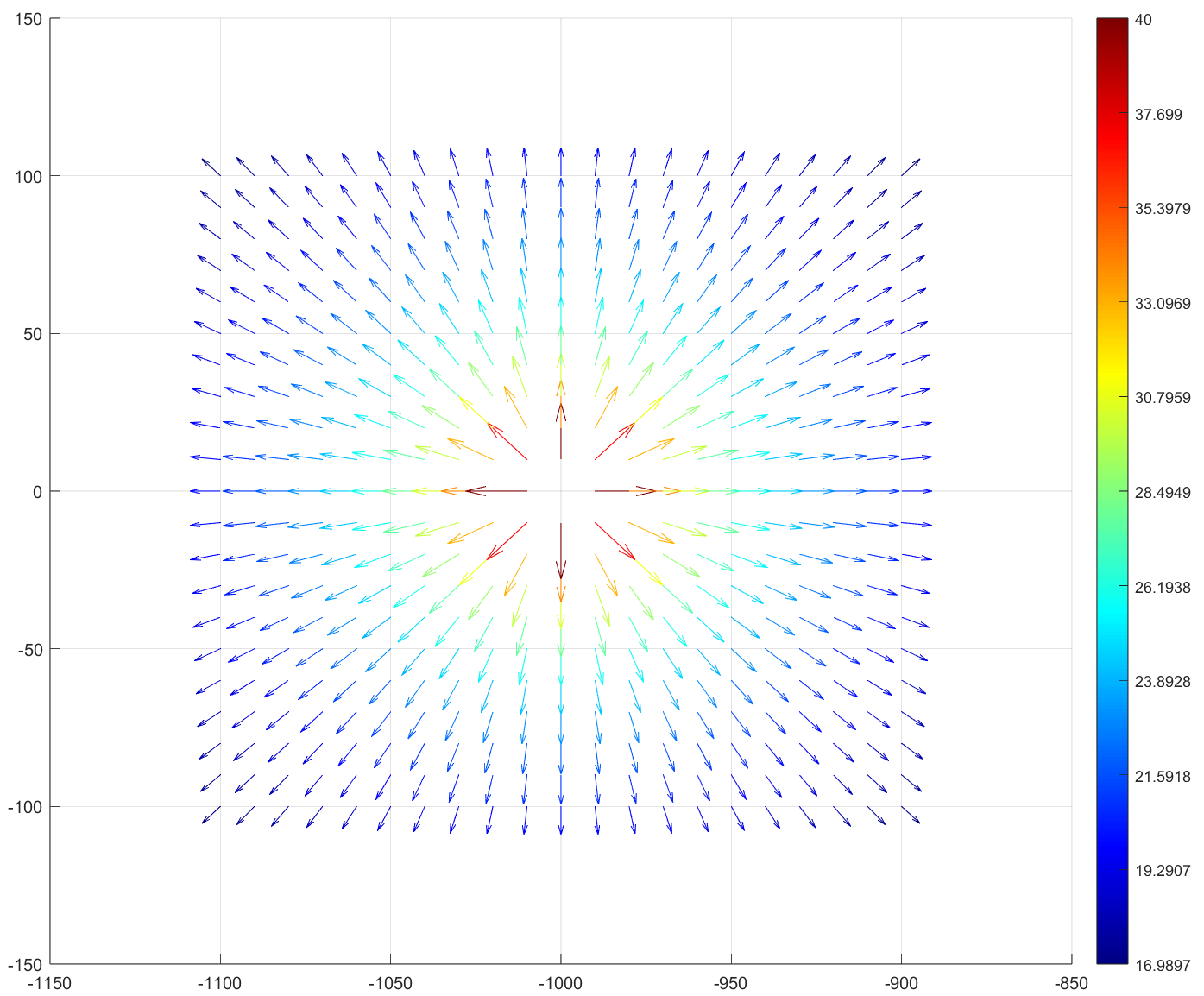
接下来看一下沿着虚数轴上的向量。

R = 1000;    %1K
C = 10^(-6); %1uF
Z1 = -1/(R*C) %极点
[X,Y] = meshgrid( 0 , -10000:500:10000 );
Z = X + 1i*Y;
H = 1./((R*C)*Z+1); %生成向量场
H_polya = conj(H);  %修改为波利亚向量场
H_r = real(H_polya);  %取实部
H_i = imag(H_polya);  %取虚部

figure(); hold on;
quiver(X,Y,H_r,H_i);
grid on;

图5.3
在这里插入图片描述
提取幅频特性曲线和相频特性曲线，请注意看脚本，没有使用波利亚向量场。

R = 1000;    %1K
C = 10^(-6); %1uF
Z1 = -1/(R*C) %极点
[X,Y] = meshgrid( 0 , 0:1:10000 );

Z = X + 1i*Y*2*pi;
H = 1./((R*C)*Z+1); %生成向量场
H_db = 20*log10(abs(H)); %转为分贝值

H_angle = angle( H );

figure();
subplot(2,1,1);
semilogx ( Y, H_db );
grid on
subplot(2,1,2);
semilogx(Y,H_angle*180/pi);
grid on

图5.4
在这里插入图片描述
看式(5.2)和图5.2可知，极点产生的的向量场，是 $1s\frac{1}{\text{s}}$ 的向量场平移到 $s1{{\text{s}}_{\text{1}}}$ 处得到。
图5.2的极点是一个源，从源中射出的箭头就像一个流体，在二维平直空间上，这种流体遵循守恒律，即对任意的内部包含一个极点的闭合曲线 $C$ ，沿着 $C$ 积分结果是 $2πi2\pi i$ 。
向量场中，距离极点越近的点 $s$ ，受到的影响越大，该点的流体密度越大，即模长越长，并且满足反比率 $1r\frac{1}{r}$ ，方向是背离极点，这方向可用和实数轴的夹角 $θ\theta$ 来表示，“ $−θ-\theta$ ”（或者说原来的场——而非波利亚向量场——在 $s$ 的形成的角度）就是相频曲线中的相位。
一个有意思的是，这种反比率 $1r\frac{1}{r}$ 和三维平直空间的平方反比率 $1r2\frac{1}{{{r}^{2}}}$ 实际上是能量守恒的体现，在其他维度的空间中也有各自的表现形式，比如一维空间，就是等比率 $1$ ，高斯定理是表述这种守恒率的数学工具。这种现象在引力学、电动力学、热力学、复分析、偏微分方程等科目被不同地表述。我们这些研究车振的，大体上属于声学的范畴，声学上有一个认识，距离每拉长一倍，功率下降6db，这实际上就是这种守恒律展现出的一个现象。想象一个点声源，声能量从源向外传播，能量可以形象地想象成一种流体，学术点叫通量（能量也好，质量也罢，我常常把它们统一想象成流体，这样一来就可以从统一的角度来看待诸如能量守恒、质量守恒等问题。这种看法其实很古老，西方的前辈曾经把热能认为是一种物质，即热质，为此聚讼纷纭）。用两个闭合曲面 ${{s}_{1}}$ 、 ${{s}_{2}}$ 去包裹源，在稳态的情况下，流经 ${{s}_{1}}$ 、 ${{s}_{2}}$ 的通量（流体） $ϕ1{{\phi }_{1}}$ 、 $ϕ2{{\phi }_{2}}$ 是相等的。不妨把曲面简化成球面 ${{s}_{1}}$ 、 ${{s}_{2}}$ ，半径分别是 ${{r}_{1}}$ 、 ${{r}_{2}}$ ，分别取球面上两个点周围的一小块面积为 $δ1{{\delta }_{1}}$ 、 $δ2{{\delta }_{2}}$ 的曲面， $δ{\delta}$ 在球面面积中的占比自然分别是 $δ14πr12\frac{{{\delta }_{1}}}{4\pi {{r}_{1}}^{2}}$ 、 $δ24πr22\frac{{{\delta }_{2}}}{4\pi {{r}_{2}}^{2}}$ ，各自通量是 $δ1ϕ4πr12\frac{{{\delta }_{1}}\phi }{4\pi {{r}_{1}}^{2}}$ 、 $δ2ϕ4πr22\frac{{{\delta }_{2}}\phi }{4\pi {{r}_{2}}^{2}}$ ，通量密度就是 $ϕ4πr12\frac{\phi }{4\pi {{r}_{1}}^{2}}$ 、 $ϕ4πr12\frac{\phi }{4\pi {{r}_{1}}^{2}}$ 。我喜欢把平方反比率写成 $14πr2\frac{1}{4\pi {{r}^{2}}}$ ，从这些公式里读者们应该能明白。于是乎两球面上的点的功率之差就是 $10log⁡10θ4πr12−10log⁡10θ4πr2210{{\log }_{10}}\frac{\theta }{4\pi {{r}_{1}}^{2}}-10{{\log }_{10}}\frac{\theta }{4\pi {{r}_{2}}^{2}}$ ，即 $20log⁡10r2r120{{\log }_{10}}\frac{{{r}_{2}}}{{{r}_{1}}}$ ，当 ${{r}_{2}}=2{{r}_{1}}$ ，得 $20log⁡10r2r1≈6db20{{\log }_{10}}\frac{{{r}_{2}}}{{{r}_{1}}}\approx 6db$ 。这些当然是题外话了，只是辅助我们对极点的认识，敲代码用不上，买菜也用不上。
回到二维的复平面中，或许读者会有疑问，对解析的复函数 $H(s)H\left( s \right)$ 的积分为什么会看成是其波利亚向量场上的积分？这个只能说是计算的结果。令 $s = x + i y$ ， $H(s)=u+ivH\left( s \right)=u+iv$ ，沿着复平面上的曲线 $γ\gamma$ 对 $H(s)H\left( s \right)$ 积分
$∫γH(s)ds=∫γ(u+iv)d(x+iy)=∫γ(udx−vdy)+i∫γ(vdx+udy)\int_{\gamma }{H\left( s \right)ds=}\int_{\gamma }{\left( u+iv \right)d\left( x+iy \right)}=\int_{\gamma }{\left( udx-vdy \right)}+i\int_{\gamma }{\left( vdx+udy \right)}$
上式右侧第一项 $∫γ(udx−vdy)=∫γ(udx+(−v)dy)\int_{\gamma }{\left( udx-vdy \right)}=\int_{\gamma }{\left( udx+\left( -v \right)dy \right)}$ ，是 $H(s)‾=u+i(−v)\overline{H\left( s \right)}=u+i\left( -v \right)$ 生成的向量场沿 $γ\gamma$ 的环量 $Γ\Gamma$ ，是内积 $γ→⋅H(s)‾\overrightarrow{\gamma }\centerdot \overline{H\left( s \right)}$ ，在物理课上，它常常别表述为功；第二项 $∫γ(vdx+udy)=∫γ(−(−v)dx+udy)\int_{\gamma }{\left( vdx+udy \right)}=\int_{\gamma }{\left( -\left( -v \right)dx+udy \right)}$ 是 $H(s)‾\overline{H\left( s \right)}$ 生成的向量场沿 $γ\gamma$ 的通量 $Φ\Phi$ ，是外积 $γ→∧H(s)‾\overrightarrow{\gamma }\wedge \overline{H\left( s \right)}$ ；而积分就变成了几何积 $γ→H(s)‾\overrightarrow{\gamma }\overline{H\left( s \right)}$ 。在这里，微积分、几何、物理完美地对应起来了。
柯西积分公式是解闭合曲线的好工具。对图5.2中的极点 ${{s}_{1}}$ ，用任意的闭合曲线 $C$ 去包围极点，沿着 $C$ 积分 $∫C1s-s1dz=2πi\int_{C}{\frac{1}{\text{s-}{{\text{s}}_{\text{1}}}}dz=}2\pi i$ ，不管 $C$ 如何变化， $Γ\Gamma$ 始终是0而 $Φ\Phi$ 始终是 $2π2\pi$ ，在物理世界中就是守恒率的体现。

5.2 零点

写出RC高通电路的传递函数，函数中存在一个极点 ${{s}_{0}}=0$ ，在此我们只谈论零点，不讨论极点。
$H(s)=RCsRCs+1(5.3)\text{H}\left( \text{s} \right)=\frac{\text{RCs}}{\text{RCs+1}}\tag{5.3}$
画出零点附近的向量场

R = 1000; %1K
C = 10^(-6); %1uF

[X,Y] = meshgrid( -2:0.4:2 , -2:0.4:2 );

Z = X + 1i*Y;
H  = ((R*C)*Z);  %生成向量场
H_r = real(H);  %取实部
H_i = imag(H);  %取虚部

figure(); hold on;
quiver(X,Y,H_r,H_i);
grid on;

图5.5
在这里插入图片描述
零点“ $s-{{s}_{0}}$ ”生成的向量场，可以看成是“ $s$ ”的向量场平移到 ${s}_{0}$ 处。
零点生成的场，可以比作弹簧，遵循胡克定律，即距离零点越近，受到的影响越小，满足正比率，方向是背离零点。反之，离得越远，影响越大，越是不稳，这也是连续系统中找不到全零点电路的原因。
零点的波利亚向量场也很有趣，如下图。
图5.6
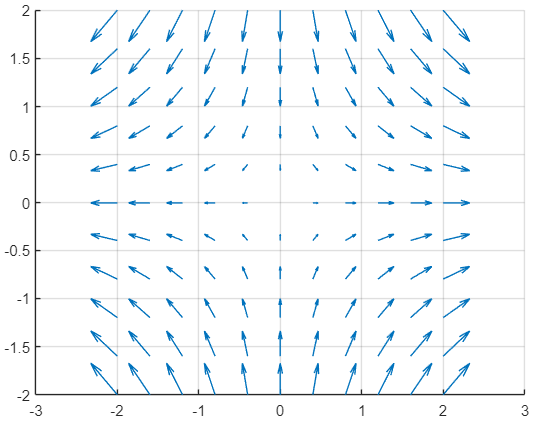
在这里插入图片描述
从图中也可以验证在复分析或者多元微积分中学到的知识，即解析函数 $H(s)=s−s0H\left( s \right)=s-{{s}_{0}}$ 生成的向量场上沿闭合曲线的积分为0。读者不妨在图上任意地方画几个圈圈，看看 $Γ\Gamma$ 如何变化， $Φ\Phi$ 如何变化。从数学上证明这一点，只需要用到格林公式和柯西-黎曼方程。