[数学基础] 正态分布：数学原理、物理意义及Python实验

原创于 2025-10-18 17:55:09 发布 · 1.3k 阅读

17 ·

CC 4.0 BY-SA版权

文章标签：

#python #开发语言 #概率论 #数学 #统计学 #信号分析

正态分布：数学原理、物理意义及Python实验

文章目录

正态分布：数学原理、物理意义及Python实验
- 1. 引言
- 2. 正态分布的数学原理
- - 2.1 概率密度函数
  - 2.2 数学特性
  - - 2.2.1 对称性
    - 2.2.2 渐近性
    - 2.2.3 拐点
    - 2.2.4 矩特性
  - 2.3 标准正态分布
  - 2.4 累积分布函数
- 3. 正态分布的物理意义
- - 3.1 中心极限定理
  - 3.2 误差理论
  - 3.3 自然界的涌现现象
- 4. Python案例演示
- - 4.1 环境准备
  - 4.2 案例1：绘制不同参数的正态分布曲线
  - 4.3 案例2：中心极限定理的模拟验证
  - 4.4 案例3：正态分布在质量控制中的应用
  - 4.5 案例4：正态分布的累积概率计算
  - 4.6 案例5：正态性检验
- 5. 结论
- - 5.1 理论意义
  - 5.2 实践价值
  - 5.3 注意事项

1. 引言

正态分布（Normal Distribution），又称高斯分布（Gaussian Distribution），是概率论与统计学中最重要、最常用的连续概率分布之一。从自然现象到社会现象，从物理测量到经济数据，正态分布无处不在。本文将深入探讨正态分布的数学原理、物理意义，并通过Python案例直观展示其特性。

2. 正态分布的数学原理

2.1 概率密度函数

正态分布的概率密度函数（Probability Density Function, PDF）由以下公式定义：

$f(x∣μ,σ2)=12πσ2e−(x−μ)22σ2f(x|\mu,\sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}$

其中：

$μ\mu$ 是均值（位置参数），决定分布的中心位置
$σ\sigma$ 是标准差（尺度参数），决定分布的离散程度
$σ2\sigma^2$ 是方差

2.2 数学特性

2.2.1 对称性

正态分布曲线关于均值 $μ\mu$ 对称，满足：
$f(μ+x)=f(μ−x)f(\mu + x) = f(\mu - x)$

2.2.2 渐近性

当 $\to \pm\infty$ 时， $\to 0$ ，即曲线以x轴为渐近线。

2.2.3 拐点

正态分布曲线在 $\mu \pm \sigma$ 处有拐点。

2.2.4 矩特性

一阶矩（均值）： $\mu$
二阶中心矩（方差）： $\sigma^2$
偏度：0（对称分布）
峰度：3（常以此为基准定义超额峰度）

2.3 标准正态分布

当 $μ=0\mu = 0$ ， $σ=1\sigma = 1$ 时，称为标准正态分布：
$φ(x)=12πe−x22\varphi(x) = \frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}$

任意正态分布都可以通过标准化变换转换为标准正态分布：
$\frac{X - \mu}{\sigma}$

2.4 累积分布函数

正态分布的累积分布函数（Cumulative Distribution Function, CDF）为：
$\Phi\left(\frac{x-\mu}{\sigma}\right) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\frac{x-\mu}{\sigma}} e^{-\frac{t^2}{2}} dt$

3. 正态分布的物理意义

3.1 中心极限定理

中心极限定理是正态分布普遍存在的理论基石。该定理指出：

独立同分布的随机变量序列，当样本量足够大时，其样本均值近似服从正态分布，且这与原始变量的分布无关。

数学表达：
设 $X_1, X_2, ..., X_n$ 是独立同分布的随机变量， $E[Xi]=μE[X_i] = \mu$ ， $Var[Xi]=σ2Var[X_i] = \sigma^2$ ，则：
$Xˉ−μσ/n→dN(0,1)\frac{\bar{X} - \mu}{\sigma/\sqrt{n}} \xrightarrow{d} N(0,1)$

3.2 误差理论

在测量领域，正态分布描述了随机误差的分布。多次测量同一物理量时，测量误差通常服从正态分布，这是由于：

误差由大量微小、独立的因素共同作用
各因素对总误差的贡献相近
正负误差出现的机会均等

3.3 自然界的涌现现象

许多自然现象近似服从正态分布，如：

人类身高：受遗传、营养、环境等多因素影响
分子运动速度：麦克斯韦-玻尔兹曼分布
测量误差：天文观测、物理实验等

4. Python案例演示

4.1 环境准备

import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
from scipy import integrate
import seaborn as sns

plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False    # 用来正常显示负号

print("环境准备完成！")

4.2 案例1：绘制不同参数的正态分布曲线

# 案例1：不同参数的正态分布比较
def plot_normal_distributions():
    """
    绘制不同均值和标准差的正态分布曲线
    """
    x = np.linspace(-10, 10, 1000)
    
    # 定义不同的参数组合
    parameters = [
        (0, 1, 'μ=0, σ=1 (标准正态)'),
        (0, 2, 'μ=0, σ=2'),
        (2, 1, 'μ=2, σ=1'),
        (-2, 1.5, 'μ=-2, σ=1.5')
    ]
    
    plt.figure(figsize=(12, 8))
    
    for mu, sigma, label in parameters:
        y = stats.norm.pdf(x, mu, sigma)
        plt.plot(x, y, label=label, linewidth=2)
    
    plt.title('不同参数的正态分布曲线', fontsize=16, fontweight='bold')
    plt.xlabel('x', fontsize=14)
    plt.ylabel('概率密度 f(x)', fontsize=14)
    plt.legend(fontsize=12)
    plt.grid(True, alpha=0.3)
    plt.axhline(y=0, color='k', linestyle='-', alpha=0.3)
    plt.axvline(x=0, color='k', linestyle='-', alpha=0.3)
    plt.show()

plot_normal_distributions()

演示结果：各种不同参数的正态分布曲线，都是典型的钟型曲线
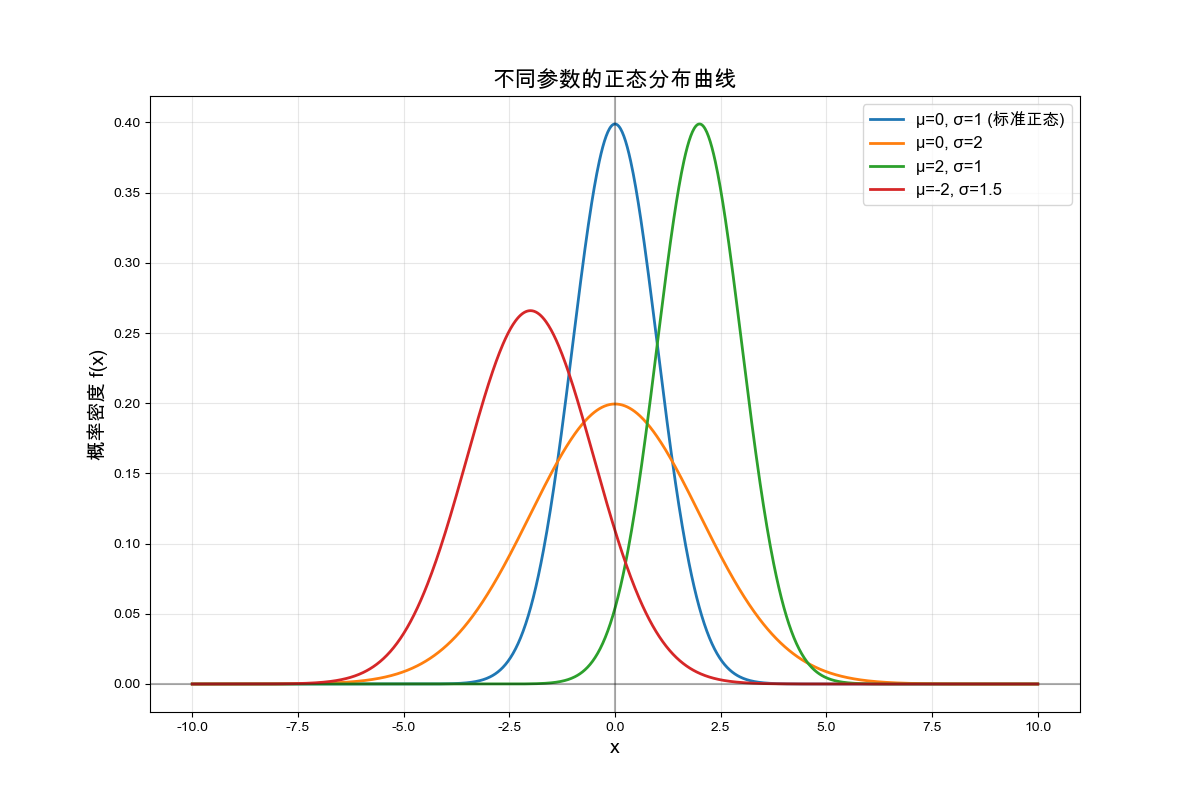
在这里插入图片描述

4.3 案例2：中心极限定理的模拟验证

# 案例2：中心极限定理演示
def central_limit_theorem_demo():
    """
    通过模拟验证中心极限定理
    """
    np.random.seed(42)
    
    # 原始分布：均匀分布
    n_samples = 10000
    sample_size = 30  # 每次抽样的样本量
    
    # 生成样本均值
    sample_means = []
    for _ in range(n_samples):
        sample = np.random.uniform(0, 1, sample_size)  # 从均匀分布抽样
        sample_means.append(np.mean(sample))
    
    # 绘制结果
    fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 6))
    
    # 原始均匀分布
    uniform_samples = np.random.uniform(0, 1, 1000)
    ax1.hist(uniform_samples, bins=30, density=True, alpha=0.7, color='skyblue')
    ax1.set_title('原始分布：均匀分布 U(0,1)', fontsize=14)
    ax1.set_xlabel('x')
    ax1.set_ylabel('密度')
    
    # 样本均值的分布
    ax2.hist(sample_means, bins=50, density=True, alpha=0.7, color='lightcoral', 
             label='样本均值分布')
    
    # 拟合正态分布
    mu = np.mean(sample_means)
    sigma = np.std(sample_means)
    x = np.linspace(min(sample_means), max(sample_means), 100)
    y = stats.norm.pdf(x, mu, sigma)
    ax2.plot(x, y, 'r-', linewidth=2, label=f'N({mu:.3f}, {sigma:.3f}²)')
    
    ax2.set_title('样本均值的分布（中心极限定理）', fontsize=14)
    ax2.set_xlabel('样本均值')
    ax2.set_ylabel('密度')
    ax2.legend()
    
    plt.tight_layout()
    plt.show()
    
    print(f"原始均匀分布的均值: 0.5")
    print(f"样本均值的均值: {mu:.4f}")
    print(f"样本均值的标准差: {sigma:.4f}")
    print(f"理论预测的标准差: {1/np.sqrt(12*sample_size):.4f}")

central_limit_theorem_demo()

演示结果：

原始均匀分布的均值: 0.5
样本均值的均值: 0.5005
样本均值的标准差: 0.0527
理论预测的标准差: 0.0527

分布图：
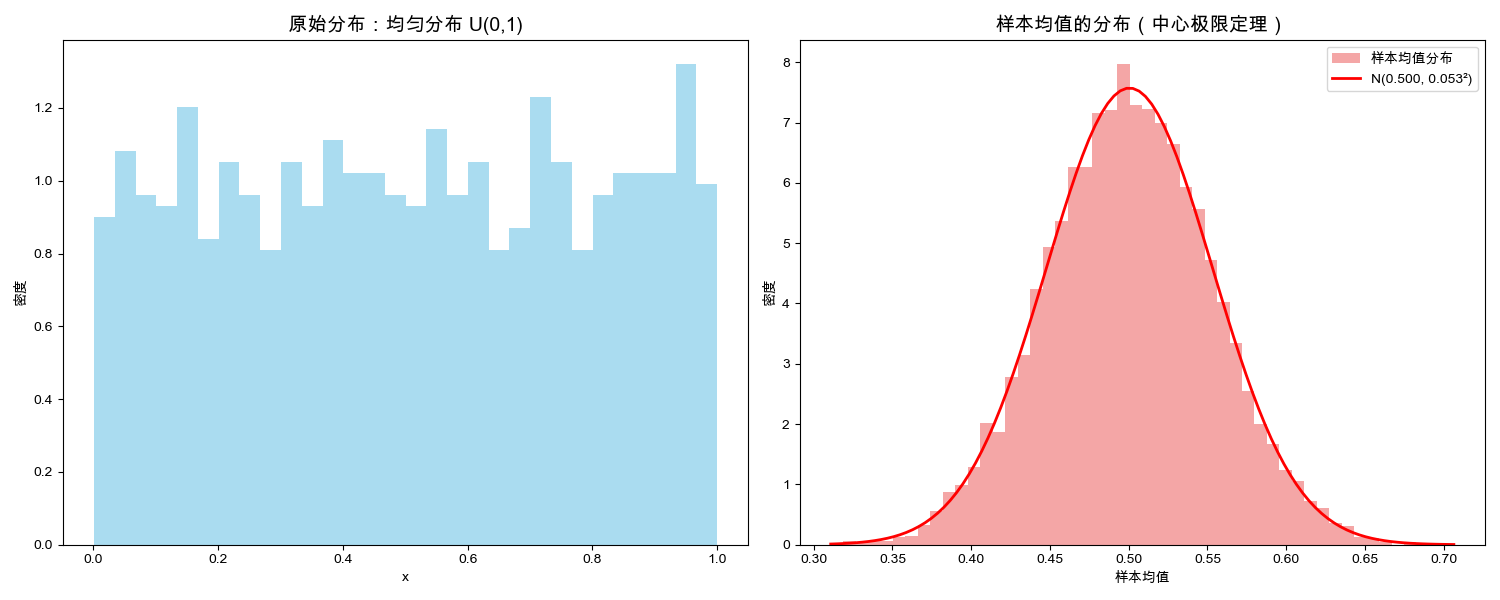
在这里插入图片描述

4.4 案例3：正态分布在质量控制中的应用

# 案例3：质量控制中的正态分布
def quality_control_demo():
    """
    演示正态分布在质量控制中的应用
    """
    np.random.seed(123)
    
    # 模拟生产线上的产品尺寸
    true_mean = 10.0  # 目标尺寸
    true_std = 0.2    # 生产波动
    
    # 生成样本数据
    samples = np.random.normal(true_mean, true_std, 1000)
    
    # 质量控制界限 (6σ原则)
    upper_limit = true_mean + 3*true_std  # 上控制限
    lower_limit = true_mean - 3*true_std  # 下控制限
    
    # 计算不合格品率
    defect_upper = np.sum(samples > upper_limit) / len(samples) * 100
    defect_lower = np.sum(samples < lower_limit) / len(samples) * 100
    total_defect = defect_upper + defect_lower
    
    # 绘制质量控制图
    plt.figure(figsize=(12, 8))
    
    # 直方图与密度曲线
    plt.hist(samples, bins=30, density=True, alpha=0.7, color='lightblue', 
             label='产品尺寸分布')
    
    # 正态分布曲线
    x = np.linspace(true_mean - 4*true_std, true_mean + 4*true_std, 100)
    y = stats.norm.pdf(x, true_mean, true_std)
    plt.plot(x, y, 'b-', linewidth=2, label='理论正态分布')
    
    # 控制界限
    plt.axvline(x=upper_limit, color='red', linestyle='--', linewidth=2, 
                label=f'上控制限: {upper_limit:.2f}')
    plt.axvline(x=lower_limit, color='red', linestyle='--', linewidth=2, 
                label=f'下控制限: {lower_limit:.2f}')
    plt.axvline(x=true_mean, color='green', linestyle='-', linewidth=2, 
                label=f'目标值: {true_mean:.2f}')
    
    # 填充不合格区域
    x_fill_upper = np.linspace(upper_limit, true_mean + 4*true_std, 100)
    y_fill_upper = stats.norm.pdf(x_fill_upper, true_mean, true_std)
    plt.fill_between(x_fill_upper, y_fill_upper, alpha=0.3, color='red', 
                     label=f'上侧不合格: {defect_upper:.2f}%')
    
    x_fill_lower = np.linspace(true_mean - 4*true_std, lower_limit, 100)
    y_fill_lower = stats.norm.pdf(x_fill_lower, true_mean, true_std)
    plt.fill_between(x_fill_lower, y_fill_lower, alpha=0.3, color='red', 
                     label=f'下侧不合格: {defect_lower:.2f}%')
    
    plt.title('产品质量控制图（基于正态分布）', fontsize=16, fontweight='bold')
    plt.xlabel('产品尺寸', fontsize=14)
    plt.ylabel('概率密度', fontsize=14)
    plt.legend(fontsize=12)
    plt.grid(True, alpha=0.3)
    plt.show()
    
    print(f"理论不合格品率: {0.27}% (3σ原则)")
    print(f"实际上侧不合格率: {defect_upper:.2f}%")
    print(f"实际下侧不合格率: {defect_lower:.2f}%")
    print(f"总不合格率: {total_defect:.2f}%")

quality_control_demo()

演示结果：

理论不合格品率: 0.27% (3σ原则)
实际上侧不合格率: 0.10%
实际下侧不合格率: 0.20%
总不合格率: 0.30%

基于正态分布的品控分析图：
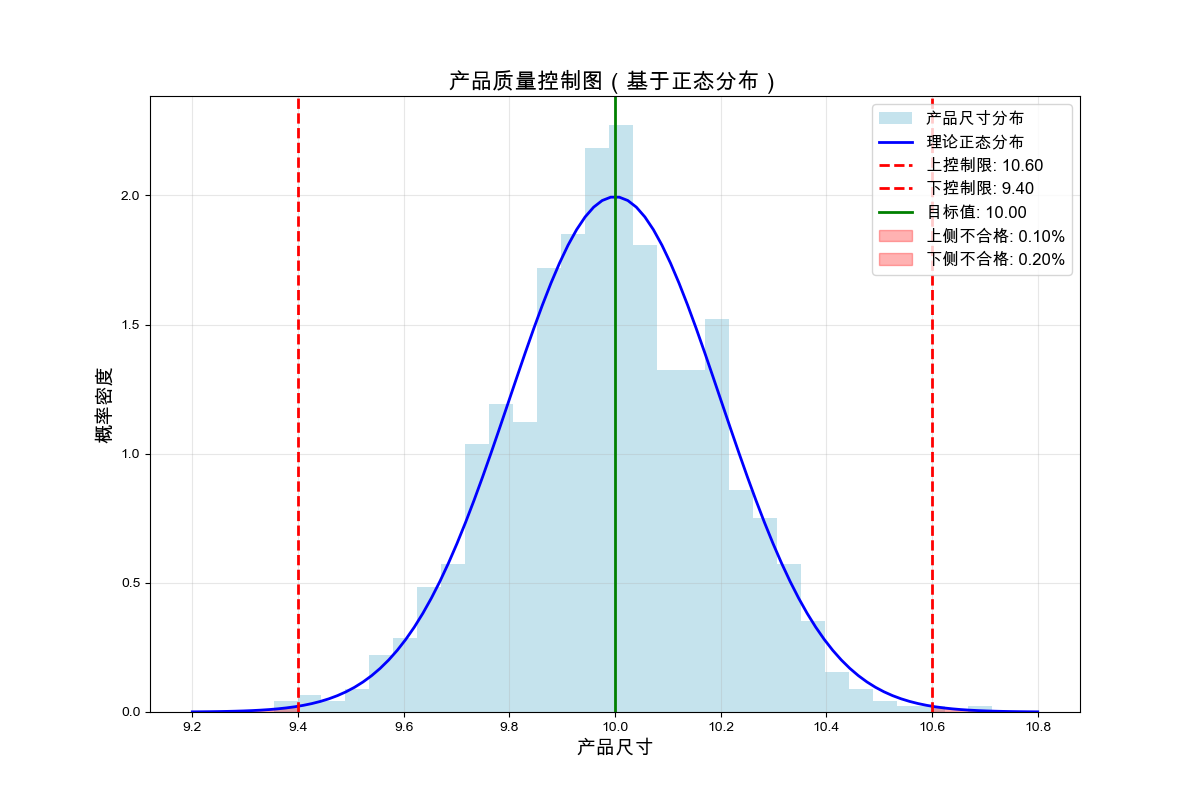
在这里插入图片描述

4.5 案例4：正态分布的累积概率计算

# 案例4：累积分布函数与概率计算
def normal_probability_calculations():
    """
    演示正态分布的概率计算
    """
    # 设定参数：假设智商测试服从正态分布
    iq_mean = 100
    iq_std = 15
    
    # 计算不同区间的概率
    prob_less_than_85 = stats.norm.cdf(85, iq_mean, iq_std)
    prob_between_85_115 = stats.norm.cdf(115, iq_mean, iq_std) - stats.norm.cdf(85, iq_mean, iq_std)
    prob_greater_than_130 = 1 - stats.norm.cdf(130, iq_mean, iq_std)
    
    # 计算百分位数
    percentile_95 = stats.norm.ppf(0.95, iq_mean, iq_std)
    percentile_99 = stats.norm.ppf(0.99, iq_mean, iq_std)
    
    # 可视化
    plt.figure(figsize=(12, 8))
    x = np.linspace(iq_mean - 4*iq_std, iq_mean + 4*iq_std, 1000)
    y = stats.norm.pdf(x, iq_mean, iq_std)
    
    plt.plot(x, y, 'b-', linewidth=2, label=f'N({iq_mean}, {iq_std}²)')
    
    # 填充不同概率区域
    # < 85
    x1 = x[x <= 85]
    y1 = stats.norm.pdf(x1, iq_mean, iq_std)
    plt.fill_between(x1, y1, alpha=0.6, color='red', 
                     label=f'IQ < 85: {prob_less_than_85*100:.1f}%')
    
    # 85-115
    x2 = x[(x >= 85) & (x <= 115)]
    y2 = stats.norm.pdf(x2, iq_mean, iq_std)
    plt.fill_between(x2, y2, alpha=0.6, color='green', 
                     label=f'85 ≤ IQ ≤ 115: {prob_between_85_115*100:.1f}%')
    
    # > 130
    x3 = x[x >= 130]
    y3 = stats.norm.pdf(x3, iq_mean, iq_std)
    plt.fill_between(x3, y3, alpha=0.6, color='purple', 
                     label=f'IQ > 130: {prob_greater_than_130*100:.1f}%')
    
    # 标记特殊点
    special_points = [85, 100, 115, 130, percentile_95, percentile_99]
    special_labels = ['85', '100(均值)', '115', '130', f'95%({percentile_95:.1f})', 
                      f'99%({percentile_99:.1f})']
    
    for point, label in zip(special_points, special_labels):
        plt.axvline(x=point, color='gray', linestyle=':', alpha=0.7)
        y_point = stats.norm.pdf(point, iq_mean, iq_std)
        plt.plot(point, y_point, 'ro', markersize=8)
        plt.text(point, y_point + 0.002, label, ha='center', fontsize=10)
    
    plt.title('智商测试的正态分布分析', fontsize=16, fontweight='bold')
    plt.xlabel('智商分数', fontsize=14)
    plt.ylabel('概率密度', fontsize=14)
    plt.legend(fontsize=12)
    plt.grid(True, alpha=0.3)
    plt.show()
    
    # 输出统计结果
    print("=== 智商测试正态分布分析 ===")
    print(f"均值: {iq_mean}, 标准差: {iq_std}")
    print(f"智商低于85的比例: {prob_less_than_85*100:.2f}%")
    print(f"智商在85-115之间的比例: {prob_between_85_115*100:.2f}%")
    print(f"智商高于130的比例: {prob_greater_than_130*100:.2f}%")
    print(f"前5%的智商分数至少为: {percentile_95:.2f}")
    print(f"前1%的智商分数至少为: {percentile_99:.2f}")

normal_probability_calculations()

演示结果：

=== 智商测试正态分布分析 ===
均值: 100, 标准差: 15
智商低于85的比例: 15.87%
智商在85-115之间的比例: 68.27%
智商高于130的比例: 2.28%
前5%的智商分数至少为: 124.67
前1%的智商分数至少为: 134.90

智商测试分布分析图：
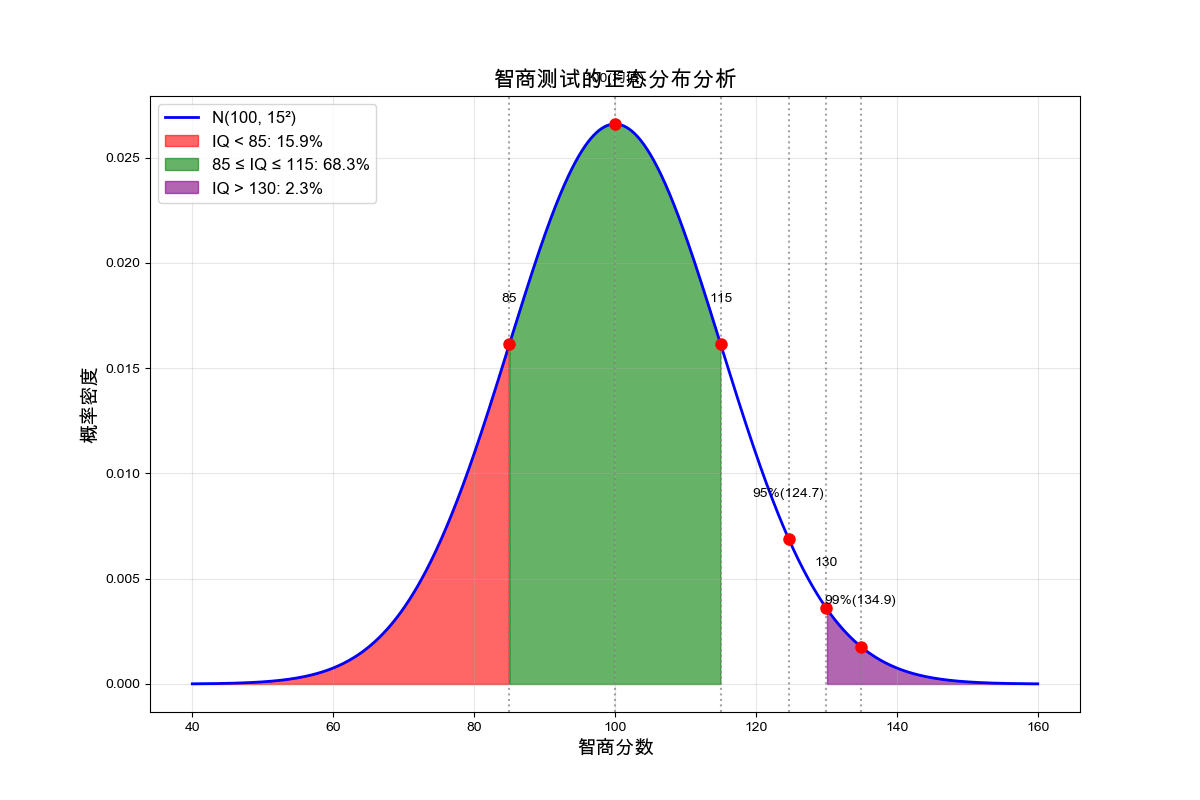
在这里插入图片描述

4.6 案例5：正态性检验

# 案例5：正态性检验
def normality_test_demo():
    """
    演示如何使用统计方法检验数据是否服从正态分布
    """
    np.random.seed(42)
    
    # 生成正态分布和非正态分布的数据
    normal_data = np.random.normal(0, 1, 1000)
    uniform_data = np.random.uniform(-3, 3, 1000)
    exponential_data = np.random.exponential(1, 1000) - 1  # 中心化
    
    datasets = [
        (normal_data, '正态分布数据'),
        (uniform_data, '均匀分布数据'),
        (exponential_data, '指数分布数据')
    ]
    
    # 进行正态性检验 (Shapiro-Wilk检验)
    print("=== 正态性检验结果 (Shapiro-Wilk检验) ===")
    print("原假设: 数据服从正态分布")
    print("显著性水平: α = 0.05")
    print("-" * 50)
    
    fig, axes = plt.subplots(2, 3, figsize=(15, 10))
    
    for i, (data, title) in enumerate(datasets):
        # 直方图与Q-Q图
        # 直方图
        axes[0, i].hist(data, bins=30, density=True, alpha=0.7, color='lightblue')
        axes[0, i].set_title(f'{title}\n直方图', fontsize=12)
        axes[0, i].set_xlabel('值')
        axes[0, i].set_ylabel('密度')
        
        # 添加正态分布曲线
        x = np.linspace(min(data), max(data), 100)
        if len(data) > 1:
            y = stats.norm.pdf(x, np.mean(data), np.std(data))
            axes[0, i].plot(x, y, 'r-', linewidth=2, label='拟合正态分布')
            axes[0, i].legend()
        
        # Q-Q图
        stats.probplot(data, dist="norm", plot=axes[1, i])
        axes[1, i].set_title(f'{title}\nQ-Q图', fontsize=12)
        
        # 正态性检验
        stat, p_value = stats.shapiro(data)
        print(f"{title:20} | 统计量: {stat:.4f} | p值: {p_value:.4f} | {'服从正态' if p_value > 0.05 else '不服从正态'}")
    
    plt.tight_layout()
    plt.show()

normality_test_demo()

演示结果：

=== 正态性检验结果 (Shapiro-Wilk检验) ===
原假设: 数据服从正态分布
显著性水平: α = 0.05
--------------------------------------------------
正态分布数据               | 统计量: 0.9986 | p值: 0.6273 | 服从正态
均匀分布数据               | 统计量: 0.9543 | p值: 0.0000 | 不服从正态
指数分布数据               | 统计量: 0.8391 | p值: 0.0000 | 不服从正态

可视化结果：
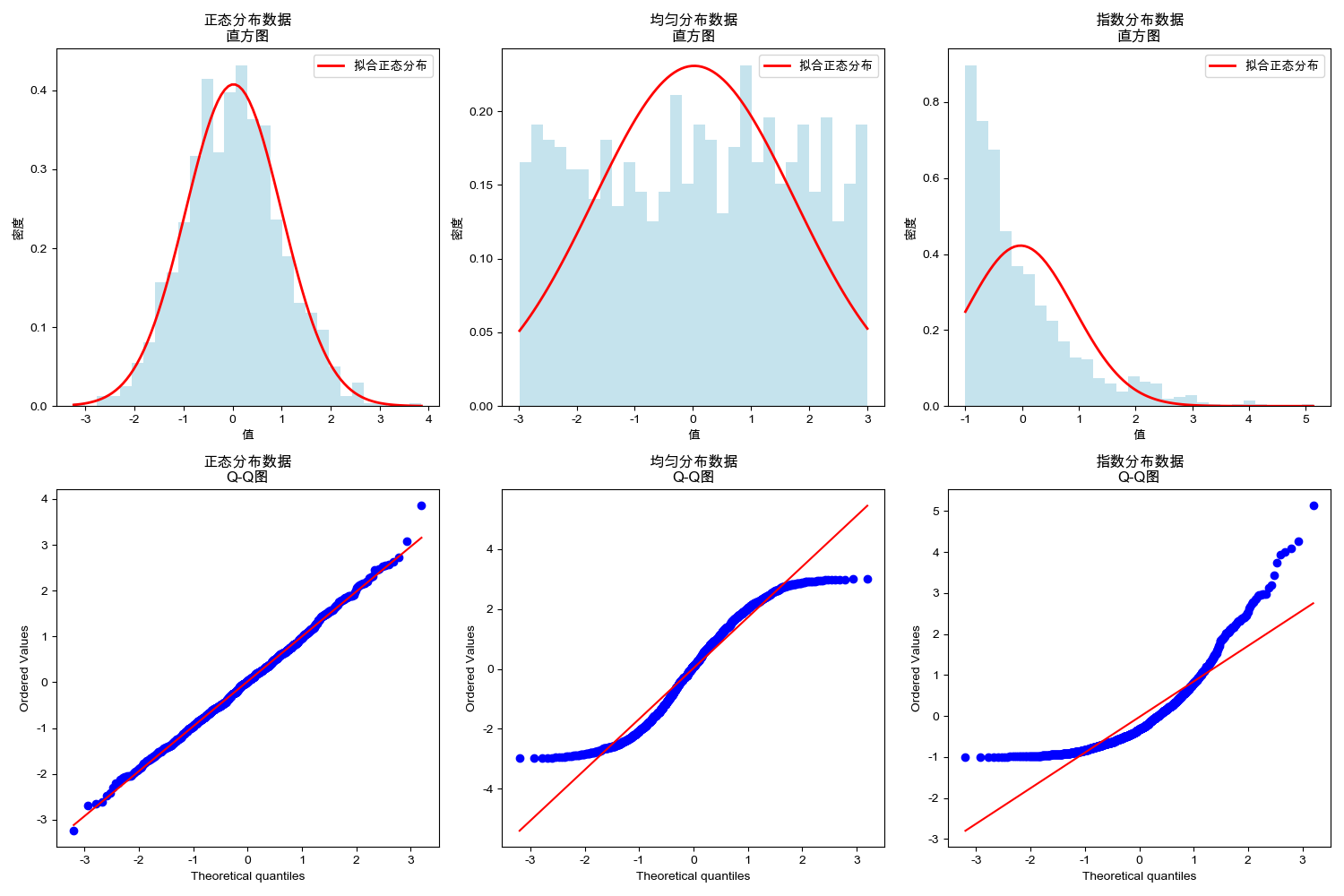
在这里插入图片描述

5. 结论

正态分布作为概率论与统计学中最重要的分布，其重要性体现在：

5.1 理论意义

中心极限定理保证了大量独立随机变量和的渐近正态性
最大熵性质：给定均值和方差，正态分布是具有最大熵的连续分布
良好的数学性质：便于解析处理和数学推导

5.2 实践价值

统计推断的基础：参数估计、假设检验等都基于正态分布假设
质量控制：6σ管理等质量改进方法的核心
风险建模：金融、保险等领域的风险评估
自然科学：测量误差、分子运动等自然现象的建模

5.3 注意事项

虽然正态分布应用广泛，但需要注意：

实际数据可能不严格服从正态分布
厚尾分布、偏态分布等需要其他分布模型
大样本下中心极限定理才有效
需要进行正态性检验来验证假设

正态分布的普适性和良好的数学性质使其成为科学研究与工程应用中不可或缺的工具。通过本文的数学原理分析和Python实践演示，希望读者能够更深入地理解和应用这一重要的概率分布。

参考文献：

Box, G. E. P., Hunter, J. S., & Hunter, W. G. (2005). Statistics for Experimenters
Montgomery, D. C. (2019). Introduction to Statistical Quality Control
Ross, S. M. (2014). Introduction to Probability and Statistics for Engineers and Scientists

代码说明：本文所有Python代码均使用标准科学计算库，可在Jupyter Notebook或Python环境中直接运行。

研究学习不易，点赞易。
工作生活不易，收藏易，点收藏不迷茫：）