并查集——（二）C++ 使用数组实现查并集功能

最新推荐文章于 2022-12-17 22:14:45 发布

原创最新推荐文章于 2022-12-17 22:14:45 发布 · 1.3k 阅读

5 ·

CC 4.0 BY-SA版权

文章标签：

#C++实现并差集 #P3367

OI 同时被 2 个专栏收录

116 篇文章

订阅专栏

并查集

7 篇文章

订阅专栏

本文详细介绍了并查集的基本概念、数据结构定义、初始化、查询及合并操作，并通过一个典型示例展示了如何使用并查集解决问题。此外，还探讨了在合并过程中可能出现的效率问题，并提出了一种通过引入rank数组进行优化的方法。

使用限制

使用数组表示查并集只能表示非负数。因为 C++ 规定数组的下标不能小于零。

数据定义

我们要根据题目的数据大小进行定义数组的大小。这里我们使用 0 ~ 1e5 的范围。

const int MAXN=1e5+4;
int parent[MAXN];

初始化

主要目的是将 parent 数组的值初始化为 -1，表示每个元素的父节点为自己。

void init() {
    memset(parent, -1, sizeof(parent);
}

查询

查询元素 x 的父节点序号。

int find_root(int x) {
    int x_root=x;//缺省父节点为自己。
    while (-1!= parent[x_root]) {//父节点的父节点不是-1，我们继续找
        x_root=parent[x_root];
    }
    return x_root;
}

合并

将元素 x 和元素 y 合并成为一个集合。返回 0，表示这两个元素已经在同一个集合；返回 1，表示合并成功。

int union_set(int x, int y) {
    //首先获得元素 x 和 y 的父节点
    int x_root=find_root(x);
    int y_root=find_root(y);

    if (x_root==y_root) {
        //父节点相同
        return 0;
    } else {
        //合并
        parent[x]=y_root;
        return 1;
    }
}

完整代码

个人喜欢讲这些东西封装在一个结构体或者类中。

typedef struct _DISJOINTSET {
    static const int MAXN=1e5+4;//这里需要根据数据范围进行修改
    int parent[MAXN];

    //结构体构造函数
    _DISJOINTSET(int size=MAXN) {
        init(size);
    }

    //初始化函数
    void init(int size=MAXN) {
        memset(parent, -1, sizeof(parent));
    }

    //查询
    int find_root(int x) {
        int x_root=x;
        while (-1 != parent[x_root]) {
            x_root = parent[x_root];
        }
        return x_root;
    }

    //合并
    int union_set(int x, int y) {
        int x_root = find_root(x);
        int y_root = find_root(y);

        if (x_root==y_root) {
            return 0;
        } else {
            parent[x]=y_root;
        }
    }
} DISJOINTSET;

模板样例

我们使用洛谷的 P3367 【模板】并查集，https://www.luogu.com.cn/problem/P3367。

本题是一个标准的查并集模板题。

AC 代码

//https://www.luogu.com.cn/problem/P3367
//【模板】并查集

#include <bits/stdc++.h>

using namespace std;

//并查集
typedef struct _DISJOINTSET {
    static const int MAXN=1e4+4;
    int parent[MAXN];//父节点

    _DISJOINTSET() {
        init(MAXN);
    }

    //初始化数据
    void init(int size=MAXN) {
        memset(parent, -1, size*sizeof(int));
    }

    //查找节点 x 的父节点
    int find_root(int x) {
        int x_root=x;
        while (-1 != parent[x_root]) {
            x_root=parent[x_root];
        }
        return x_root;
    }

    //将节点 x 和节点 y 合并
    int union_set(int x, int y) {
        int x_root=find_root(x);
        int y_root=find_root(y);

        if (x_root==y_root) {
            //不需要合并
            return 0;
        } else {
            parent[x_root]=y_root;
            return 1;
        }
    }
} DISJOINTSET;

int main() {
    int n,m;
    cin>>n>>m;

    DISJOINTSET myDS;

    for (int i=0; i<m; i++) {
        int op,x,y;
        cin>>op>>x>>y;

        if (1==op) {
            //合并
            myDS.union_set(x, y);
        } else if (2==op) {
            //查询
            int x_root=myDS.find_root(x);
            int y_root=myDS.find_root(y);
            if (x_root==y_root) {
                cout<<"Y\n";
            } else {
                cout<<"N\n";
            }
        }
    }

    return 0;
}

优化

在并集的时候，我们每次都是讲元素 x 的父节点设置为 y。使用这样的模板来实现并集的时候，可能出现一个极端的样例。我们用数据来说明，同样我们的数据集是 1 ~ 8。

问题所在

在极端数据情况下，parent 的深度将达到非常恐怖地步。

初始状态

这样，我们的集合为。对应的 parent 数组值为：

parent[1]=-1;
parent[2]=-1;
parent[3]=-1;
parent[4]=-1;
parent[5]=-1;
parent[6]=-1;
parent[7]=-1;
parent[8]=-1;

合并 1 和 2

我们的集合变为。对应的 parent 数组值为：

parent[1]=2;
parent[2]=-1;
parent[3]=-1;
parent[4]=-1;
parent[5]=-1;
parent[6]=-1;
parent[7]=-1;
parent[8]=-1;

合并 2 和 3

我们的集合变为。对应的 parent 数组值为：

parent[1]=2;
parent[2]=3;
parent[3]=-1;
parent[4]=-1;
parent[5]=-1;
parent[6]=-1;
parent[7]=-1;
parent[8]=-1;

合并 3 和 4

我们的集合变为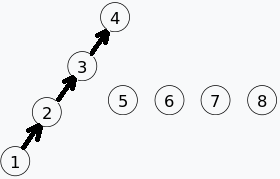。对应的 parent 数组值为：

parent[1]=2;
parent[2]=3;
parent[3]=4;
parent[4]=-1;
parent[5]=-1;
parent[6]=-1;
parent[7]=-1;
parent[8]=-1;

合并 4 和 5

我们的集合变为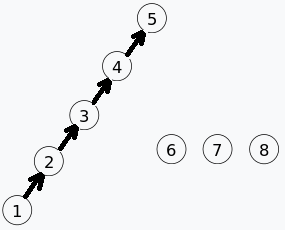。对应的 parent 数组值为：

parent[1]=2;
parent[2]=3;
parent[3]=4;
parent[4]=5;
parent[5]=-1;
parent[6]=-1;
parent[7]=-1;
parent[8]=-1;

合并 5 和 6

我们的集合变为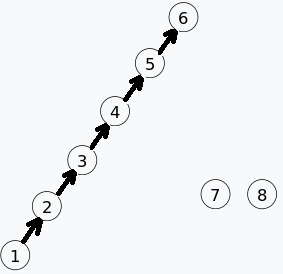。对应的 parent 数组值为：

parent[1]=2;
parent[2]=3;
parent[3]=4;
parent[4]=5;
parent[5]=6;
parent[6]=-1;
parent[7]=-1;
parent[8]=-1;

合并 6 和 7

对应的 parent 数组值为：

parent[1]=2;
parent[2]=3;
parent[3]=4;
parent[4]=5;
parent[5]=6;
parent[6]=7;
parent[7]=-1;
parent[8]=-1;

合并 7 和 8

对应的 parent 数组值为：

parent[1]=2;
parent[2]=3;
parent[3]=4;
parent[4]=5;
parent[5]=6;
parent[6]=7;
parent[7]=8;
parent[8]=-1;

我们可以看到，这个 parent 的深度不断变大。如果 N=1e5 的话，parent 树的深度将达到恐怖的 1e5-1。这样对于 find_root() 就是一个及其耗时的工作。

优化方案

从上面数据分析可知，主要的问题是在合并时候，没有考虑到 parent 树深度问题。

那么优化的方法也很简单，增加一个数组用来表示深度，也就是 rank[i]=5，表示节点 i 的 parent 树深度为 5。

每次在合并树的时候，我们选择深度较小的分支进行合并，这样不会增加 parent 树的深度。只有等深度一样的时候，我们才任选一个分支进行合并。

优化后代码

请注意 rank 数组和 union_set() 函数，经过这样的优化，parent 树的最大深度为 logN。

typedef struct _DISJOINTSET {
    static const int MAXN=1e4+4;
    int parent[MAXN];//父节点
    int rank[MAXN];//层数

    _DISJOINTSET() {
        init(MAXN);
    }

    //初始化数据
    void init(int size=MAXN) {
        memset(parent, -1, size*sizeof(int));
        memset(rank, 0, size*sizeof(int));
    }

    //查找节点 x 的父节点
    int find_root(int x) {
        int x_root=x;
        while (-1 != parent[x_root]) {
            x_root=parent[x_root];
        }
        return x_root;
    }

    //将节点 x 和节点 y 合并
    int union_set(int x, int y) {
        int x_root=find_root(x);
        int y_root=find_root(y);

        if (x_root==y_root) {
            //不需要合并
            return 0;
        } else {
            if (rank[x_root]>rank[y_root]) {
                parent[y_root]=x_root;
            } else if (rank[x_root]<rank[y_root]) {
                parent[x_root]=y_root;
            } else {
                parent[x_root]=y_root;
                rank[y_root]++;
            }
            return 1;
        }
    }
} DISJOINTSET;