新型双永磁电机设计与优化

一种用于电动汽车应用的新型双永磁电机的设计与优化

摘要

本文提出了一种用于电动自动导引车（AGV）的新型直驱式双永磁电机。所提出的电机在定子上采用分体齿结构，并在定子和转子两侧均布置永磁体，有助于降低转矩脉动并提升输出转矩。对所提出电机的气隙磁场进行了理论分析，并得出了槽/极选择指南。仿真结果展示了气隙磁通密度，其傅里叶变换（FFT）分析结果与理论分析结果吻合良好。此外，研究了设计参数对所提出电机性能的影响，发现减小定子槽开口可提高效率并降低转矩脉动。所提出电机在整个运行范围内的效率相对较高。研制了相应的样机，实验验证了设计的可行性。

索引术语 —游标永磁电机，双永磁，直接驱动，高效率。

一、引言

WITH 随着对环境保护的日益关注以及石油资源的日 益短缺，许多研究人员和汽车公司正致力于开发更高效、更可靠的推进系统[1]。电机作推进系统的关键部件，受到了前所未有的重视。通常，在汽车中，电机需要具备更高的性能和更低的生产成本。针对电动汽车应用提出了多种不同的电机。高速感应电机和同步电机结合减速齿轮箱最先得到应用。然而，齿轮箱会为推进系统引入额外的噪声和振动，并且由于在过转矩条件下可能发生故障，从而降低系统的可靠性。为克服这些问题，已开发出消除齿轮箱的直驱电机。

针对直接驱动应用提出了多种类型的电机，而永磁体（PM）因其能够利用永磁体实现高转矩和高功率密度，成为理想的选择[2]–[4]。在[4]–[6]中，对采用分布绕组和集中绕组的电机进行了比较。结论表明，采用集中绕组的电机具有较低的铜损、更高的效率、更低的齿槽转矩以及优异的容错能力。然而，对于采用集中绕组的传统多极永磁电机而言，定子槽数通常接近转子极数。当转子极数增加时，这将导致定子槽数过大，不可避免地增加槽漏磁通并降低槽满率，从而降低效率并提高制造成本。为解决此问题，引入了磁通调制（FM）效应[7]。

近年来，磁通调制效应得到了研究，在基于FM的电机中发现，转子上的小旋转角度可导致气隙磁场[8]–[11]发生大角度变化。绕组极对数不必等于转子极对数，这将显著减少多极电机的定子槽数。文献[8]研究了一种双机械端口双向磁通调制永磁电机，该电机被提出用于混合动力汽车中的电无级变速器（E‐CVT），具有两个转子和三层气隙。该电机可视为传统同步永磁电机与一个作为双向磁通调制电机的功能部分的组合。通过这种结构，可取代传统E‐CVT中的行星齿轮。在[9]中提出了用于低速高推力应用的磁通调制直线电机。结果表明，与传统电机相比，FM电机在低速下产生的推力可达其4.7倍。在[10]中分析了用于推进系统的FM电机的磁力，而这一点通常在大多数文献中未被考虑。验证表明，通过磁通调制效应可在低速下获得较大的转矩。但大多数FM电机结构复杂且具有多层气隙，导致其体积庞大且制造成本较高。仅具有单气隙的永磁游标电机（PMVM）是这些电机的一种有前景的替代方案。这类游标电机同样基于磁通调制效应运行，但其定子齿充当调制铁件，转子充当低速转子，定子槽中的绕组则充当高速转子。目前已提出多种不同的PMVM，总体上可分为三类：定子永磁游标电机（SPMVM）[12]–[14]、转子永磁游标电机（RPMVM）[15],[16]以及双永磁游标电机（DPMVM）。SPMVM仅在定子中设置永磁体，RPMVM仅在转子中设置永磁体，而DPMVM在定子和转子中均设有永磁体。在这三种类型的电机中，由于DPMVM在定子和转子上均有永磁体，能够实现双向磁通调制效应，因此相比SPMVM和RPMVM可产生更高的转矩[17]。DPMVM最早于[8]中提出，并因其在低速工况下的优异转矩密度而被众多研究人员进一步发展。在[19]中提出了一种DPMVM，并对不同DPMVM进行了比较。在[20]中研究了定子永磁体位置对DPMVM性能的影响。此外，在[21]中提出了混合励磁DPMVM。在[22]中研究了DPMVM的不同槽极组合。

本文提出并优化了一种用于自动导引车（AGV）的新型双永磁可变磁阻电机（DPMVM），其定子采用分齿结构。AGV通常以低速运行，需要较大的牵引转矩，同时要求制造成本低、效率尽可能高以及转矩脉动小。所提出的电机在效率和转矩脉动方面表现出相对优异的性能。本文的结构安排如下：首先介绍电机结构，然后分析磁场特性及槽/极选择指南。在第三节中，针对不同转子极数的电机，从效率、转矩脉动和永磁体利用率（输出转矩/永磁体用量）等方面进行分析与比较，并从中选定一种设计方案进行进一步优化，最终的优化结果也在第三节中给出。第四节详细分析所提出电机的性能。第五节展示了样机制作过程及实验结果。

II. 电机结构和工作原理

A. 电机结构

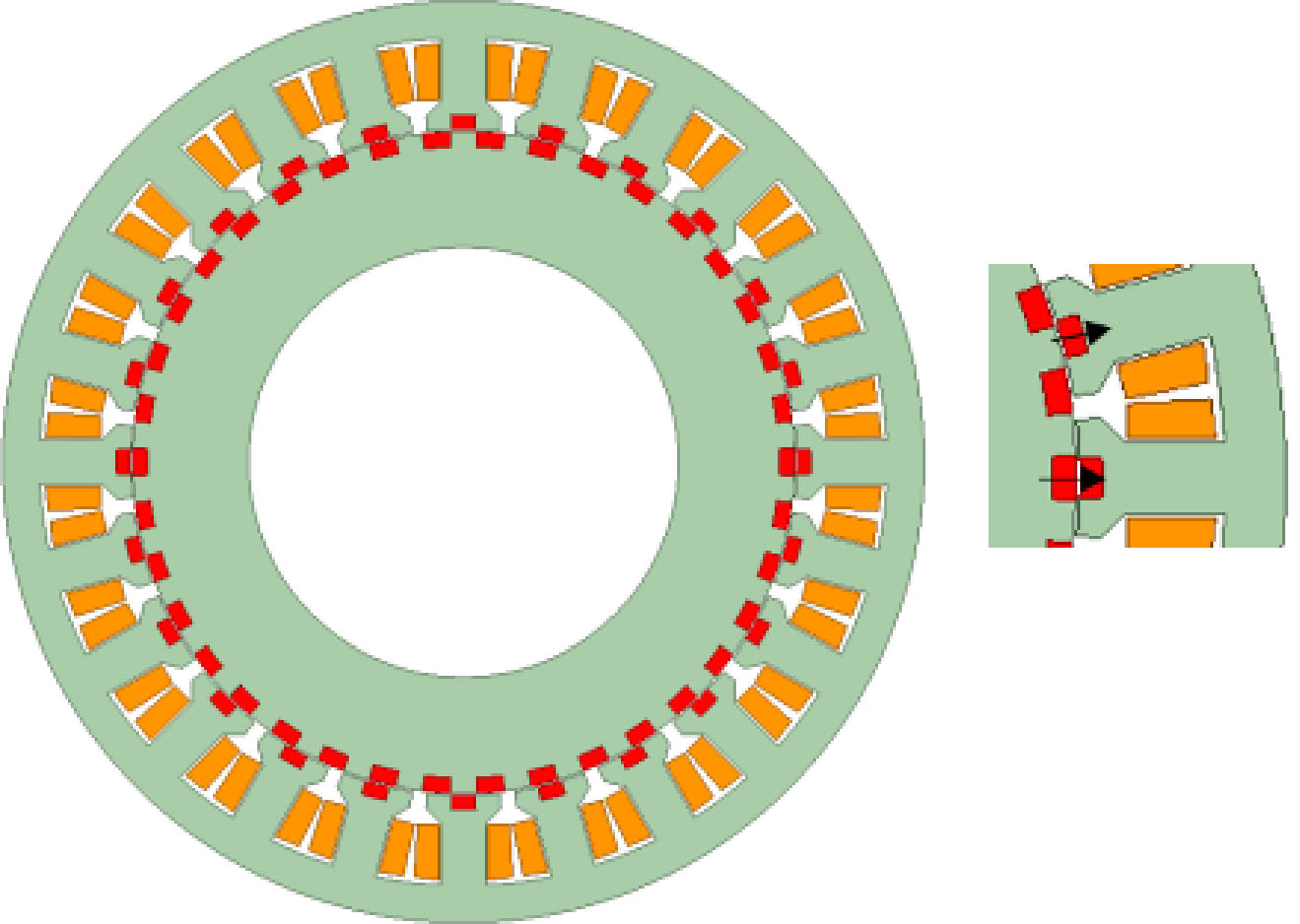
所提出的双永磁可变磁阻电机的结构如图1所示。该电机具有一个定子和一个转子，且两部分均装有永磁体。永磁体被插入到定子齿中，定子永磁体位于定子齿的中部，将一个定子齿分成了两个小齿。两部分中的永磁体均为径向充磁，并具有与图中箭头所示相同的充磁方向。所提出的电机采用双层集中绕组，以减小端部长度、铜用量以及铜损。图1所示样机电机具有24个定子槽数和38对转子极对数。绕组极对数为10。槽/极选择指南将在后文给出。后文将对具有24个定子槽和不同转子极对数的电机进行分析和比较。表I给出了本文中电机的整体设计参数。自动导引车的额定转速为95转/分钟，额定功率为1.1千瓦。自动导引车的最高转速为140 rpm，其功率仍为1.1 kW。自动导引车的转矩‐速度曲线如图2所示。

B. 工作原理

双永磁可变磁阻电机（DPMVM）的工作原理基于磁齿轮效应。转子的微小运动可引起气隙中特定极对的磁通发生巨大变化。DPMVM可视为定子永磁电机和转子永磁电机的组合。其中，转子永磁电机具有相同的定子结构，但去除了定子上的永磁体；而定子永磁电机则采用相同的转子设计，仅保留凸极，并去除了转子永磁体。关键在于，定子和转子凸极齿的调制使得定子和转子永磁体产生的磁场在气隙中产生丰富的磁场谐波。本文将对气隙磁通密度的各分量进行分析，并研究磁场主分量的旋转速度。

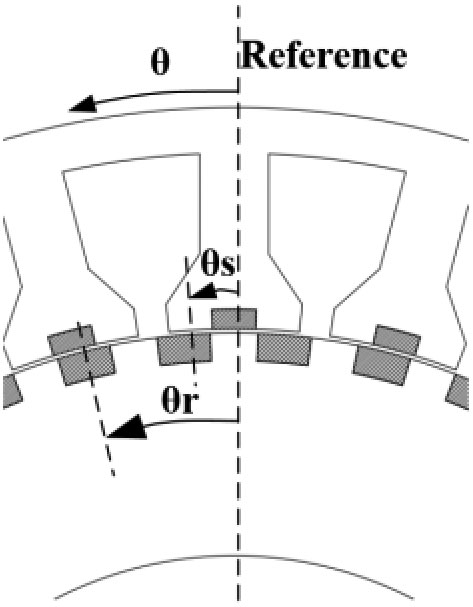
首先，假设转子和定子磁场的正向旋转方向为逆时针方向。如图3所示，θ是一个与旋转无关的空间角度变量速度和时间。θs 是参考线与定子齿中心线之间的夹角。θr 是转子中心线与参考线之间的夹角。θr 等于
$$
θr= ωt+ θr0 \quad (1)
$$

当只有转子永磁体时，由转子永磁体产生的磁动势（MMF）可以表示为
$$
Fr(θ)= \sum_{n1=1}^{+\infty} \frac{Fr_n1}{n1} \cos[n1pr(θ − θr)] \quad (2)
$$
其中，Fr 是转子永磁体的磁动势，Fr˙n1 是第n1次谐波磁动势的幅值，Fr˙1 是基波磁动势的幅值，其等于
$$
Fr_1= \frac{Brhr μr}{4 π} \quad (3)
$$

转子永磁体到定子侧的磁导
$$
λs(θ)= λs0+ \sum_{n2=1}^{+\infty} \frac{λs_n2}{n2} \cos[n2q(θ − θs)] \quad (4)
$$
其中λs0是气隙的总磁导，λs˙n2是n2次谐波的幅值。而 q是定子齿总数，等于定子槽数（Ns）乘以分割数（Nsplit）。
$$
q= Ns × Nsplit \quad (5)
$$

根据公式(2)–(4)，仅考虑基波磁动势时，由转子永磁体在气隙中产生的磁通密度为
$$
Bair_r(θ)= Fr(θ)λs(θ) ≈ Fr_1 · \cos[pr(θ − θr)] ·{λs0+ λs_1 · \cos[q(θ − θs)]}
= Fr_1 · λs0 · \cos[pr(θ − θr)]+ Fr_1 · λs_1 · \cos[pr(θ − θr)] · \cos[q(θ − θs)]
= Fr_1 ·{λs0 · \cos[pr(θ − θr)]+ \frac{λs_1}{2} ·{\cos[(pr+ q)θ −(prθr+ qθs))] +\cos[(pr − q)θ −(prθr − qθs)]}} \quad (6)
$$

电枢绕组一个极距范围内的磁通量是
$$
Φ w_r(θ)= rl ∫ {0}^{\pi / (q − p r)} B air_r(θ)dθ
= rlF r_1 \left{ \frac{λ s 0}{p r} \sin[pr(θ − θ r)]
+ \frac{λ s _1}{2(pr + q)} \sin[(pr + q)θ −(pr θ r + qθs)]
+ \frac{λ s _1}{2 (pr − q)} \sin[(pr − q)θ −(pr θ r − qθs)] \right} \bigg| {0}^{\pi / (q − p r)} .
(7)
$$

由于电枢绕组的极对数为(pr‐q)，其主要作用部分为第三项。因此，电枢绕组一个极对范围内的主磁通为
$$
Φ w _ r(θ)= rlF r _1 · \frac{λr _1}{dt} \sin[(pr − q)θ −(pr θ r − qθs)] \bigg|_{0}^{\pi / (q − p r)}
= rlFr_1 · \frac{λr_1}{(pr − q)} \sin(prθr − qθs) \quad (8)
$$

由Φw˙r可推导出一相中的反电动势如下
$$
ew_r(t)= k(q −pr)Nc\frac{dΦw_r}{dt}
= k(q −pr)NcrlFr_1 λs_1 \frac{pr − q}{d[\sin(prθr − qθs)]}{dt} = kNcrlFr_1λs_1prω \cos(prωt+ prθr0 − qθs)\quad(9)
$$
其中 θr0为转子的初始位置。类似地，对于仅存在定子永磁体的定子‐永磁体电机，其区别在于定子是静止的。由定子永磁体产生的磁动势以及气隙的磁导可表示如下
$$
Fs(θ)= \sum_{n3=1}^{+\infty} \frac{Fs_n3}{n3} \cos[n3qθ] \quad (10)
$$
$$
λr(θ)= λr0+ \sum_{n4=1}^{+\infty} \frac{λs_n4}{n4} \cos[n4pr(θ − θr)] \quad (11)
$$

气隙磁通密度和电枢绕组一个极距范围内的磁通分别如公式(12)和(13)所示。
$$
Bair_s(θ)= Fs(θ)λr(θ) ≈ Fs_1 · \cos(qθ)·{λr0+ λr_1 · \cos[pr(θ − θr)]}
= Fs_1 · λr0 · \cos(qθ)+ Fs_1 · λr_1 · \cos(qθ)· \cos(prθ)−prθr
= Fs_1 · λr0 · \cos(qθ) + \frac{Fs_1 · λr_1}{2}{\cos[(q+ pr)θ −prθr] +\cos[(q −pr)θ+ prθr]} . \quad (12)
$$
$$
Φw_s(θ)= rl∫ {0}^{\pi / (q − p r)} Bair_s(θ)dθ= rlFs_1 \left{ \frac{λ r 0}{q} \sin(qθ)+ \frac{λ r _1}{2(pr +q)} \sin[(pr+q)θ−prθr] + \frac{λ r _1}{2(q − pr)} \sin[(q −pr)θ+ prθr] \right} \bigg| {0}^{\pi / (q − p r)} \quad (13)
$$

主有效磁通部分是第三项，其极对数与电枢绕组相同。因此，磁通可进一步表示为
$$
Φ w_s( θ) ≈ rlF s_1 \frac{λ r_1}{2(q −pr)} \sin[(q −pr) θ+ pr θ r] \bigg|_{0}^{\pi / (q − p r)}
= rlF s_1 \frac{λ r_1}{2(q −pr)} {\sin(π+ pr θ r) − \sin(pr θ r)}
= −rlF s_1 \frac{λ r_1}{(q −pr)} \sin(pr θ r) \quad (14)
$$

由定子永磁体在一相中产生的反电动势可如下获得
$$
e w _ s( t)= \frac{k(q −pr) N c dΦ w _ s}{dt}
= −kNcrlFs_1λr_1 \frac{d \sin(prωt+ prθr0)}{dt}
= −kNcrlFs_1λr_1prω \cos(prωt+ prθr0) \quad (15)
$$

根据公式(8)和(14)，由定子和转子永磁体在一相中产生的反电动势为
$$
ew(t)= ew_r(t)+ ew_s(t) = − kNcrl{Fr_1λs_1prω \cos(prωt+ prθr0 − qθs) +Fs_1λr_1prω \cos(prωt+ prθr0)}
= − kNcrl ·(Fr_1λs_1prω+ Fs_1λr_1prω) · \cos(prωt+ prθr0) \quad (16)
$$

C. 槽/极选择标准

根据公式(6)和(12)，气隙磁通密度的极对数（pB˙air）可以表示为
$$
pB_air= \begin{cases}
n1pr \
n1pr ± n2q \
n3q \
n3q ± n4pr
\end{cases} \quad n1, n2, n3, n4= 1, 2, 3.... \quad (17)
$$

得出结论：当电枢绕组的极对数为(q-pr)，且其频率(f w)等于
$$
fw= \frac{prω}{2π}= \frac{(q −pr)ω · pr}{(q−pr)}{2π} \quad (18)
$$

电枢绕组产生的磁场将与定子和转子永磁体产生的磁场相互耦合。并且电枢绕组的极对数（pw）可以设计得远小于pr。这样，即使采用集中绕组，也可以减少定子槽数。此外，由式(17)可知，具有（q-pr）极对的磁场的旋转速度为 ωpr/(q-pr)。由此可得齿轮比的定义，即
$$
Gr= \frac{pr}{(q −pr)} \quad (19)
$$

同样值得注意的是，当电枢绕组的极对数为(pr+ q)，且电枢绕组的频率为
$$
fw= \frac{prω}{2π}= \frac{(pr+ q)ω · p r}{(pr + q)}{2π} \quad (20)
$$

稳定的输出转矩也可以实现。并且定子和转子永磁体均对输出转矩有贡献。然而，在此条件下，pw甚至大于pr。这不利于减少定子槽数。当电枢绕组的极对数为pr，且频率为
$$
fw = \frac{pr ω}{2π} \quad (21)
$$

仅能利用转子永磁体，而定子上的永磁体将变得无用。该电机变为传统的继极式转子永磁电机。因此，双永磁体电机的槽极选择准则可以总结为
$$
pw = q −pr \quad (22)
$$

III. 设计优化

在本节中，对所提出的电机进行优化。首先，比较了具有不同转子极对数但相同定子槽数和分体齿的电机的性能。本部分对比了四种电机。四种电机的槽极组合如下面的表II所示。对于24槽的电机，当绕组极对数为10、11、13和14时，集中绕组的绕组系数较高。同时，为了满足公式(22)，转子极对数分别设置为34、35、37和38。四种电机的齿轮比也在表II中给出。其中，M I是MachineI的简称。

A. 对比研究

本部分对四种电机的性能进行了比较。为了实现公平比较，不仅四种电机的尺寸和输入功率相同，而且永磁体和铜的总体积也保持一致，定子结构同样保持不变。唯一变化的是转子极对数。整体比较结果如表III所示。可以看出，随着转子极对数的增加，四种电机相反电动势的均方根（RMS）值逐渐增大。其中M III的THD值在四种电机中最低。THD值的计算方法如下：
$$
T HD=\sqrt{\sum_{n=2}^{H} \left(\frac{V_n}{V_1}\right)^2} \quad (23)
$$
其中H和n为谐波次数，V1 是基波的值，Vn是高次谐波的值。

效率根据公式(24)计算。
$$
η= \frac{Toω}{Toω+ Pcore+ Pcopper + Pstray} \quad (24)
$$
其中，To为输出转矩，ω为旋转速度，Pcore为铁芯损耗，Pcopper为铜损，Pstray为所提出的电机的估计杂散损耗。估计的杂散损耗为额定功率的2%，对于所提出的电机为22 W。

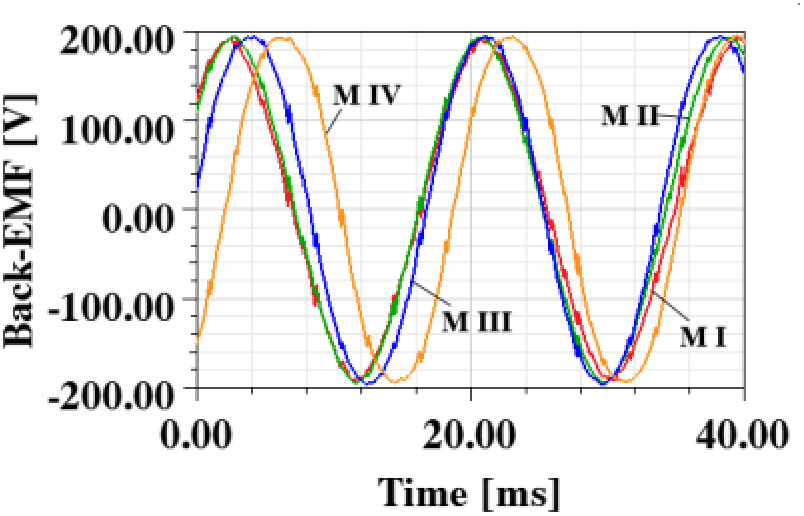
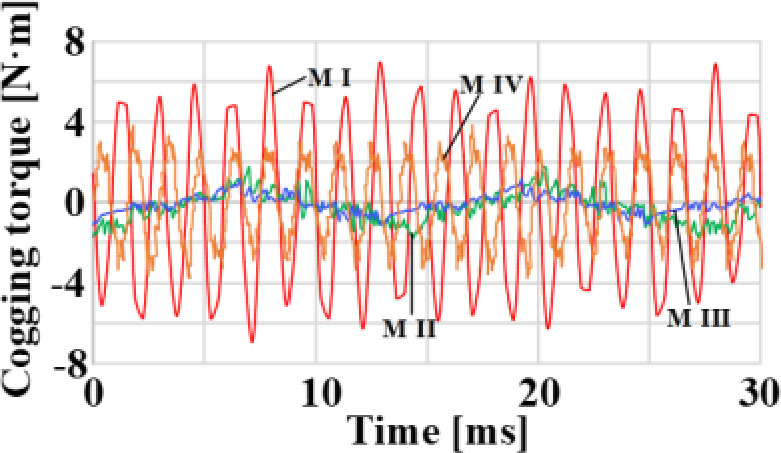
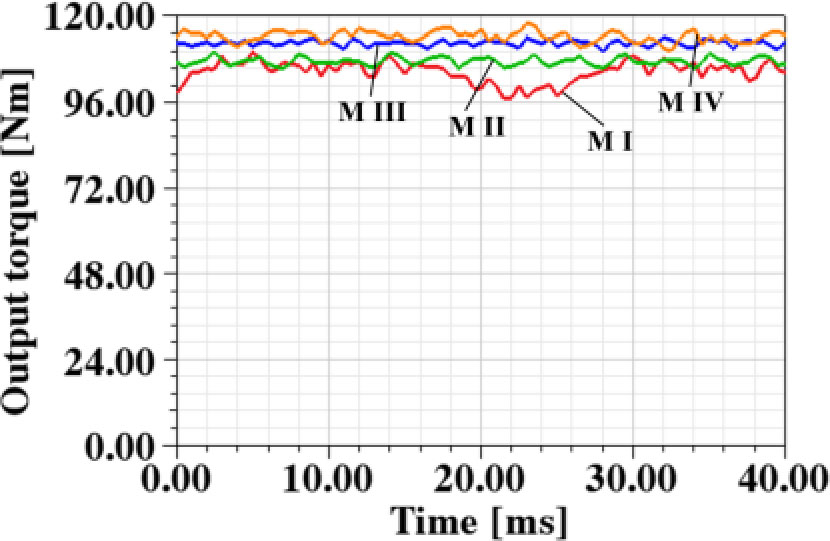
反电动势波形如图4所示。图5展示了四种电机的齿槽转矩。齿槽转矩的峰峰值列于表III中。可以看出，机器I的齿槽转矩在这四种电机中最高，而电机II的齿槽转矩最低。输出转矩的波形如图6所示。可以看出，机器I的转矩脉动最大，且其平均值在四种电机中最低。转矩脉动由仿真结果获得，等于转矩峰峰值与平均转矩之比。电机IV的输出转矩在这四种电机中最高。由于这四种电机的永磁体用量相同，因此电机IV的永磁体利用率在四种电机中最高，同时其效率也是最高的。值得注意的是，电机IV的转矩脉动为6.5%，属于可接受范围。因此，选择电机IV进行进一步研究与优化。

效率和转矩脉动随 Angleslot变化的情况。(b) 效率和转矩脉动随SPMratio变化的情况。(c) 效率和转矩脉动随Anglerpm变化的情况。(d) 效率和转矩脉动随STthick变化的情况。(e) 效率和转矩脉动随Din变化的情况。)

一种用于电动汽车应用的新型双永磁电机的设计与优化

III. 设计优化

B. 参数分析

在本部分中，研究了主要结构变量对电机性能的影响，特别是额定点下的效率和转矩脉动。并根据研究结果设定了各变量的优化范围。

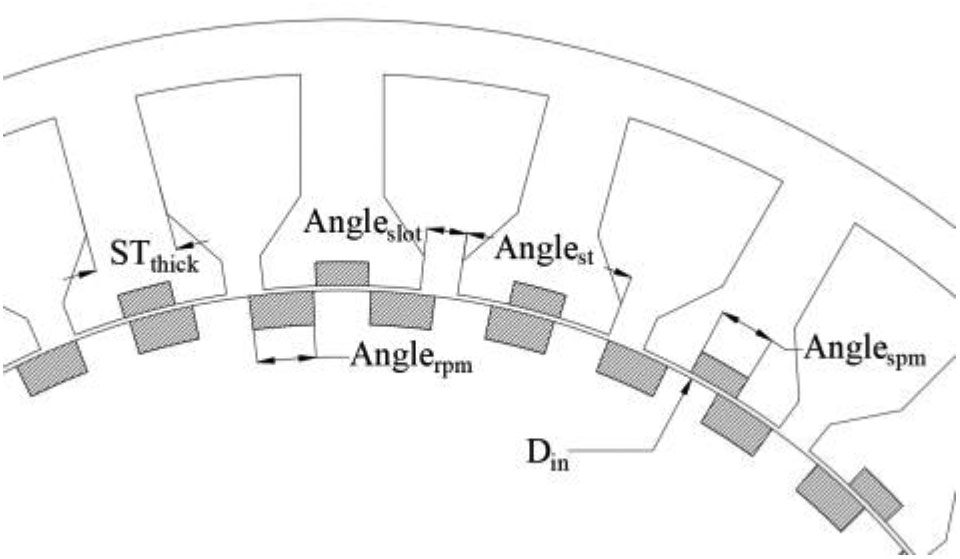
主要结构参数如图7所示。各参数含义如下：STthick：定子齿厚度；Anglerpm：转子永磁体角度；Angleslot：定子槽角度；Anglest：大定子齿内表面角度；Anglespm：定子永磁体角度；Din：定子内径；SPMratio：Anglespm除以Anglest。

图8(a)展示了在额定转速下，效率和转矩脉动随Angleslot变化的情况。可以看出，效率随着Angleslot的增加而降低，并且转矩脉动随着Angleslot的增加而增大。Angleslot越小，效率和转矩脉动性能越好。然而，Angleslot不能过小，以免影响定子绕组的自动加工。因此，Angleslot的优化范围设定为2到3度。对于SPMratio，由图8(b)可知，效率起初随着SPMratio的增加而上升；当SPMratio大于0.5后，效率开始下降。对于转矩脉动，当SPMratio在0.3至0.4之间时，其值波动较小并保持在较低水平。综合考虑效率和转矩脉动，SPMratio的优化范围设定为0.3至0.5。图8(c)显示了Anglerpm的影响。效率起初随着Anglerpm的增加而提高，当Angle超过5.5度后则基本不再变化。对于转矩脉动，在3.4至5.5度之间，其值保持在较低水平（≤5%）。同时考虑效率表现，Anglerpm的优化范围设定为4至5.5度。

对于STthick，从图8(d)可以看出，效率随着STthick的增加先上升，随后随着STthick的进一步增加而下降。转矩脉动则随着STthick的增加先减小，并在STthick继续增加时趋于稳定。因此，STthick的优化范围设定为8至13毫米。对于Din，当内径Din小于222毫米时，效率高于86.5%。转矩脉动随着Din的变化而波动。因此，Din的优化范围设定为216至222毫米。各参数的优化范围总结于表IV中。

C. 设计优化

本部分对所提出的电机进行优化。在优化过程中，输入电流保持不变，且随着槽总面积的变化，电枢绕组的空间也随之变化。槽满率保持不变，因此铜损将相应发生变化。最优模型的选择标准如公式(25)所述
$$
\begin{cases}
T_o \geq 110N \cdot m \
F= w_1Efficiency+ w_2Triple
\end{cases} \quad (25)
$$
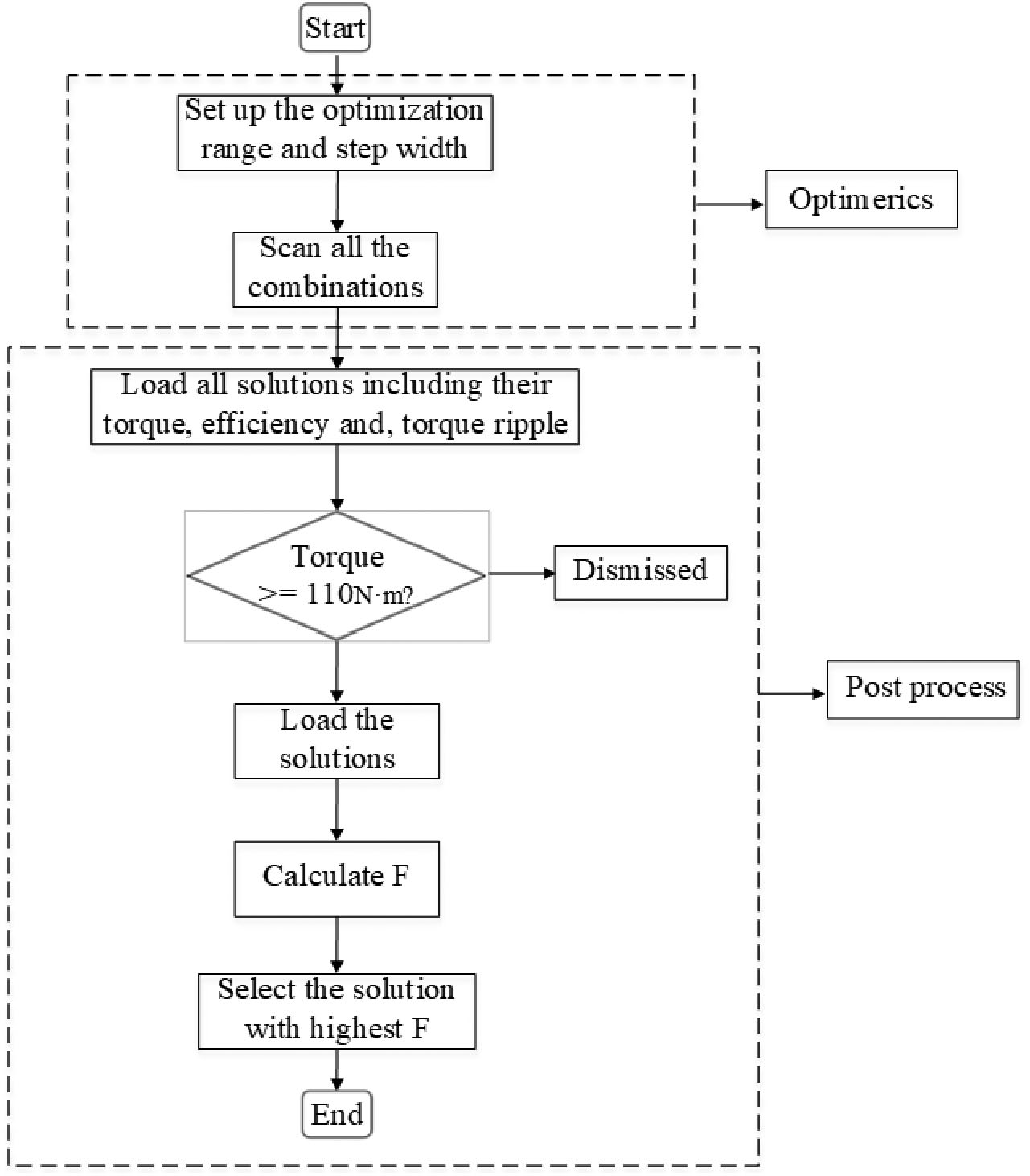
其中，To为额定输出转矩，Triple为转矩脉动，w1和w2为权重系数。采用流程图说明优化过程，如图9所示。

首先，设定表IV中参数的优化范围和步长。然后扫描所有组合，并获取包括输出转矩、效率和转矩脉动在内的结果。通过后处理，筛选出转矩高于110 N·cm的解，结果如图10所示。进一步选择最优解，根据公式(25)的第二个方程确定最优解。图10中用圆圈标出了最优解。最优解处的效率为89.7%，转矩脉动为5.5%。主要设计参数的值见表V。

IV. 性能分析

本部分研究了优化后的电机的性能。展示了空载和负载性能。负载性能包括额定转速和超速。

A. 空载

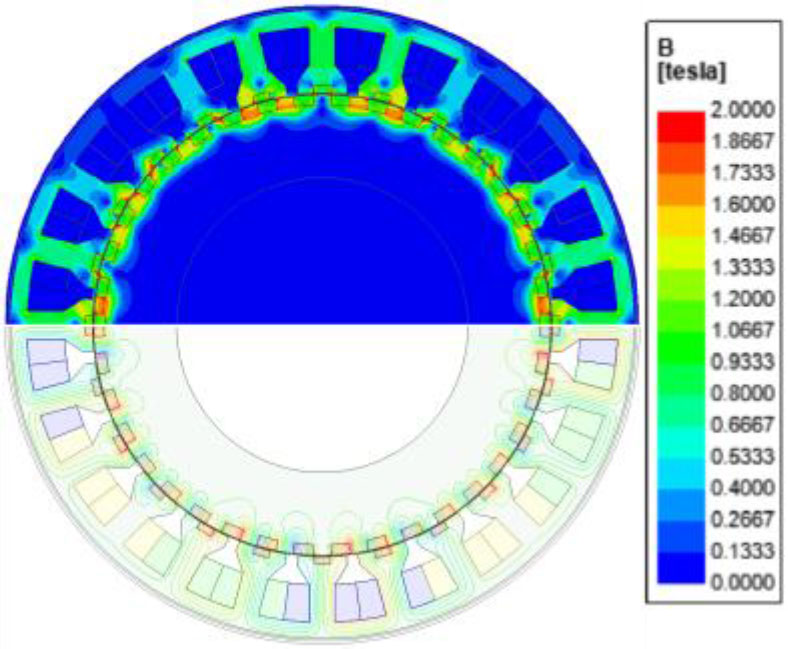
图11显示了空载磁场分布，包括磁通密度和磁力线分布。平均气隙磁通密度为0.82 T，与传统表面贴装式永磁电机和内置式永磁电机相比相对较高。对于相同尺寸和内径的传统电机，该值约为0.4至0.6 T。

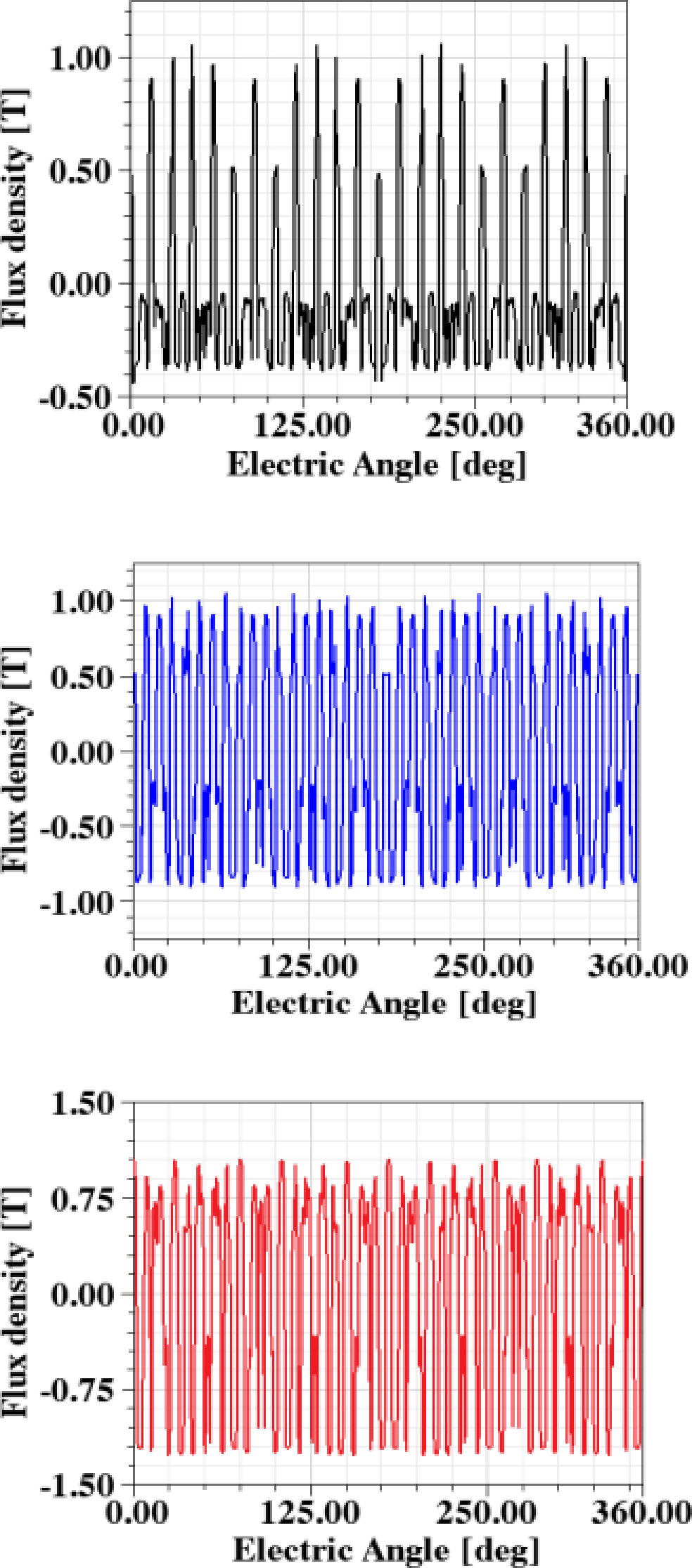
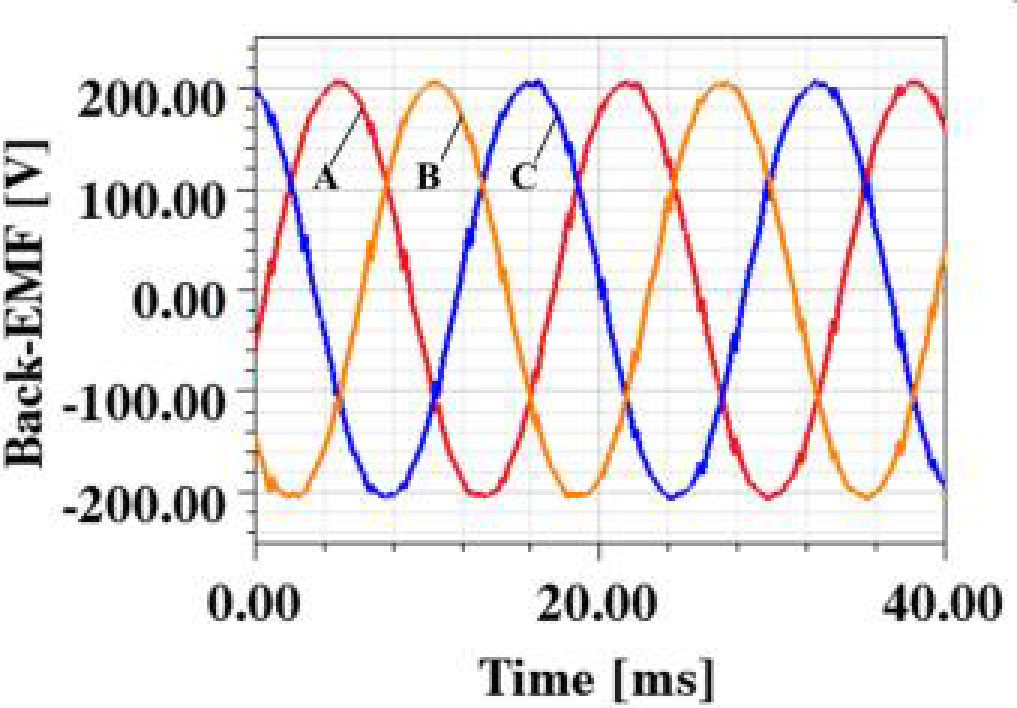
各部分永磁体产生的气隙磁通密度波形如图12所示。图12(a)和(b)显示了由定子永磁体产生的气隙磁通密度。快速傅里叶分析表明，气隙中的磁通极对数包含10、14、24、38、48。当仅存在转子永磁体时，气隙磁通密度波形如图12(c)所示，其FFT结果如图12(d)所示。主分量为10和38极对。当定子和转子永磁体同时存在时，磁通密度及其谐波分量如图12(e)和(f)所示。主分量为10th,14th, 24th, 38th, 48th谐波分量。这些结果与第II节公式(17)中的理论结果一致。图13显示了三相反电动势波形。其有效值为145 V，THD值为0.84%。

B. 负载

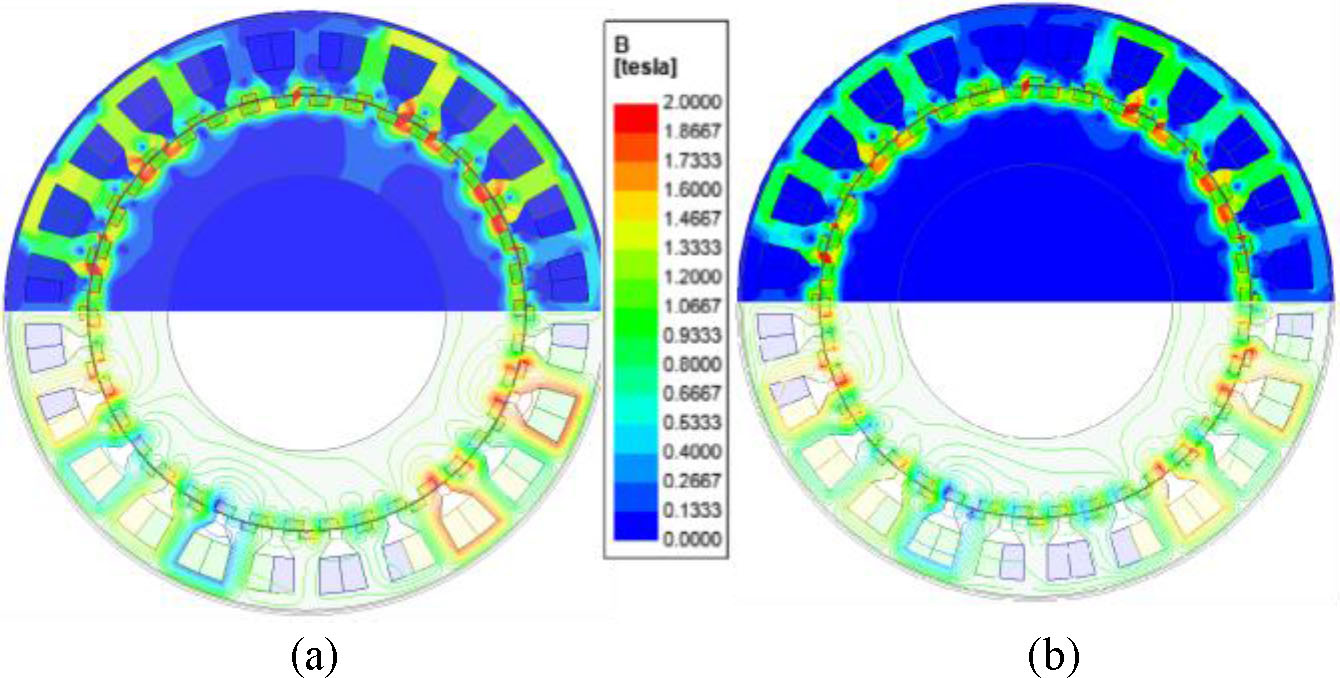
所提出的电机的负载磁场如图14所示。图14(a)显示了A相电压最大时的位置，图14(b)显示了电压为零时的位置。可以看出，转子仅移动了一个非常小的角度，等于2.4度，电角度变化了90度。

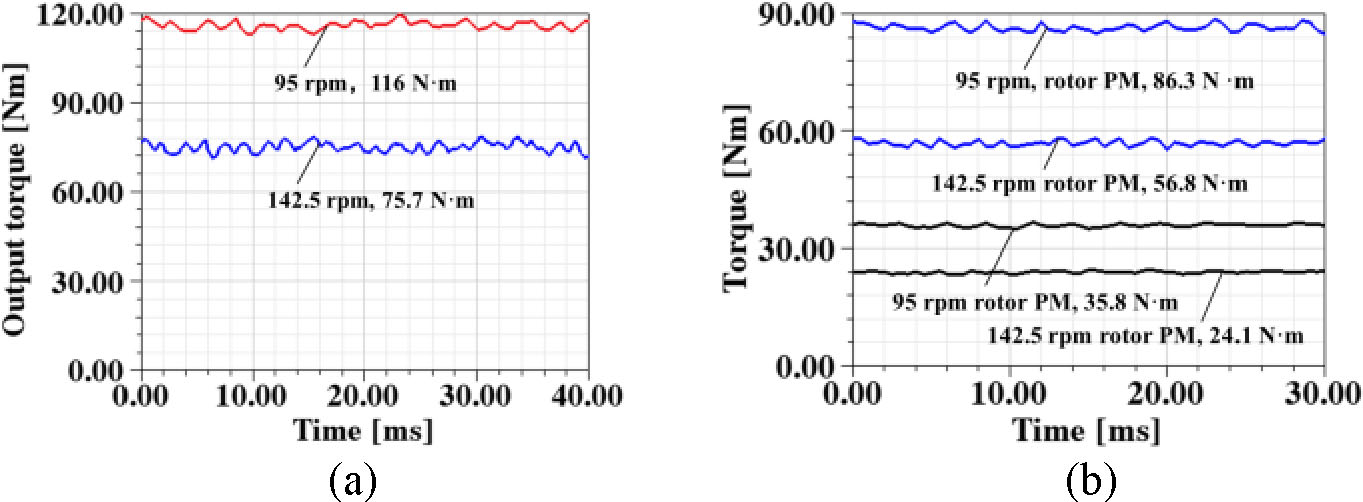
在额定转速95转/分钟和超速142.5转/分钟时的输出转矩如图15(a)所示。额定转速下的转矩脉动为5.5%，142.5转/分钟时的转矩脉动为8.4%。由于定子永磁体和转子永磁体产生的输出转矩如图15(b)所示。可以发现，当转速为95转/分钟时，由定子永磁体和转子永磁体产生的转矩比例分别为29.4%和70.6%；而在142.5转/分钟时，比例分别为29.7%和70.3%。

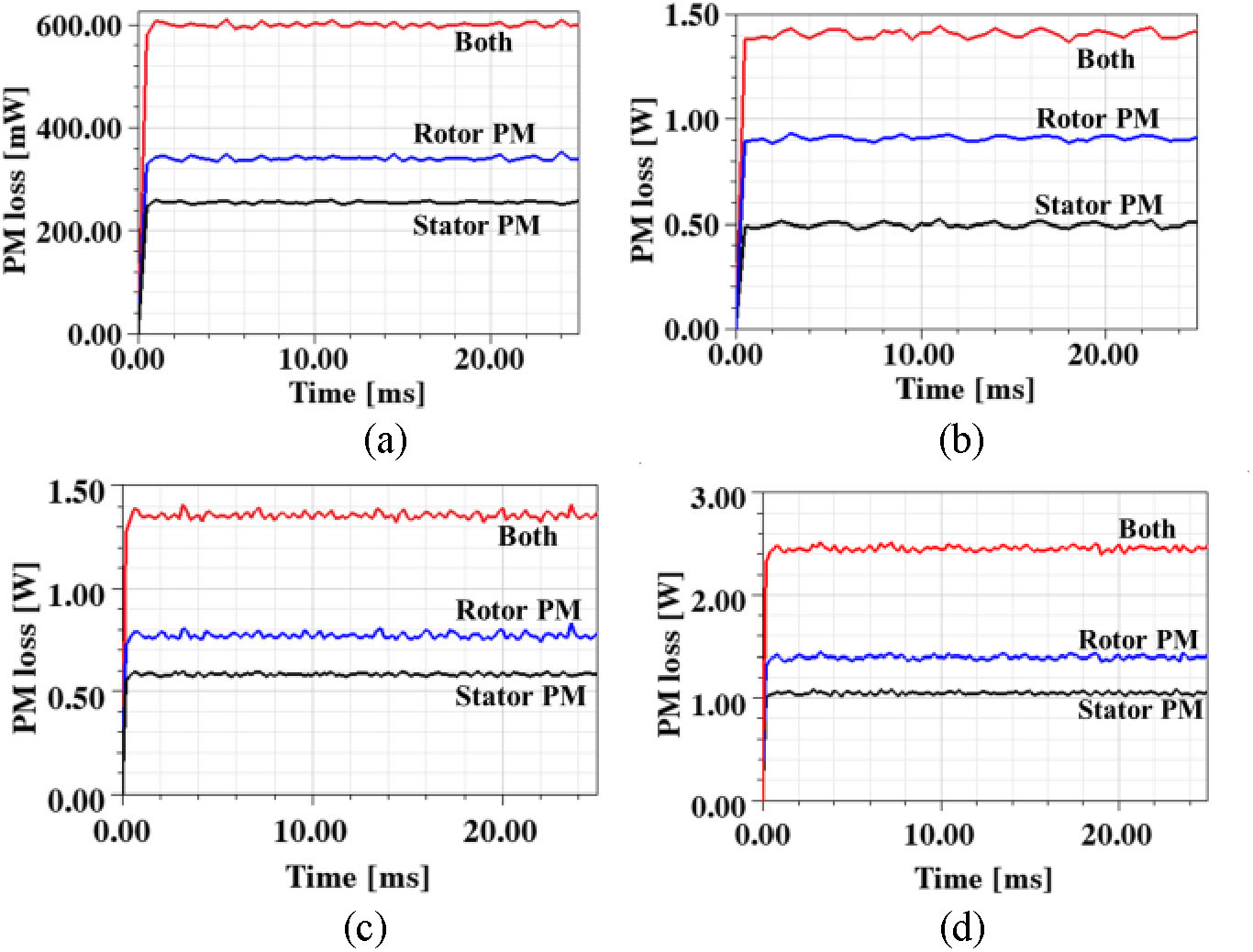
在95转/分钟和142.5转/分钟下对定子永磁体和转子永磁体中的涡流损耗进行了分析。结果如图16所示。当转速为95转/分钟时，永磁体的空载涡流损耗为0.6瓦特。其中定子永磁体和转子永磁体的损耗分量分别为0.26瓦（42.5%）和0.34瓦（57.5%）。负载状态下定子永磁体的涡流损耗为0.5瓦（35.5%），转子永磁体为0.91瓦（64.5%）。在142.5转/分钟时，定子永磁体和转子永磁体的空载涡流损耗分别为0.58瓦（42.7%）和0.77瓦（57.3%）。负载状态下的总涡流损耗为2.13瓦，其中定子和转子永磁体的损耗分别为0.81瓦（37.1%）和1.32瓦（61.9%）。可以发现，当转速从95转/分钟增加到142.5转/分钟时，定子永磁体中涡流损耗比例略有上升。在两种转速下，转子永磁体的损耗均大于定子永磁体。两种转速下的铁芯损耗和铜损如图17所示。可以看出，当转子转速为95转/分钟时，铜损是铁芯损耗的3.7倍；当转速为142.5转/分钟时，铜损是铁芯损耗的1.56倍。

95转/分钟时的空载涡流损耗。(b) 95转/分钟时的负载涡流损耗。(c) 142.5转/分钟时的空载涡流损耗。(d) 142.5转/分钟时的负载涡流损耗。)

V. 实验验证

制造了一台样机以验证所提出的电机的性能。图18展示了定子铁芯、转子铁芯、定子组件和样机。图19展示了测试台。使用一台伺服电机作为负载。

图20(a)显示了样机空载线反电动势的仿真和实验波形，两者整体上具有良好的一致性。实验结果比仿真结果低5.2%，且实验波形上存在毛刺，主要由信息噪声引起。图20(b)给出了仿真线反电动势与实验反电动势的THD值。仿真反电动势的THD值为0.89%，相对较低；实验反电动势的THD值为1.03%，略高于仿真值。

所提出的双永磁电机的负载输出转矩如图21所示。实际输入电流为3.4 A，高于仿真值3.2 A。实验输出转矩为111 N·cm。这是由于实验反电动势较低所致。142.5转/分钟时的电流为2.5 A。实验测得的输出转矩为75.8 N·m。可以发现，实验的转矩脉动低于仿真结果。实际上，转矩脉动受伺服电机的影响。如果伺服电机体积大且重量重，则其惯性较大，转矩脉动就会较小。这就是为什么实验的转矩脉动低于仿真结果的原因。通过功率分析仪测得的输入功率和扭矩传感器测得的输出功率，可得95转/分钟时的实验效率为88%，142.5转/分钟时的效率为91.1%。

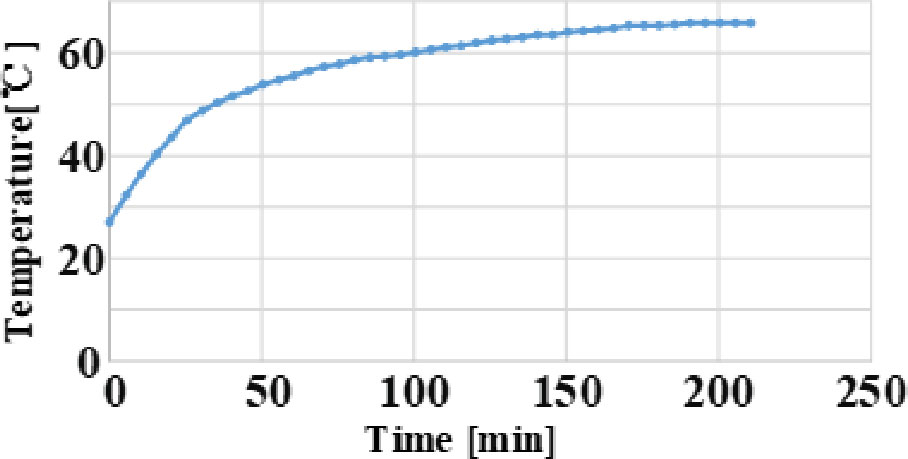
当旋转速度为95rpm时，样机的温升如图22所示。该数据从定子电枢绕组测得。电机的冷却方式为自然冷却。可以注意到，前30分钟内温升较快，之后升温速率降低。该温度在220分钟后趋于稳定。最终稳定在65.8 °C。环境温度为27.1 °C。温升为38.7 K。

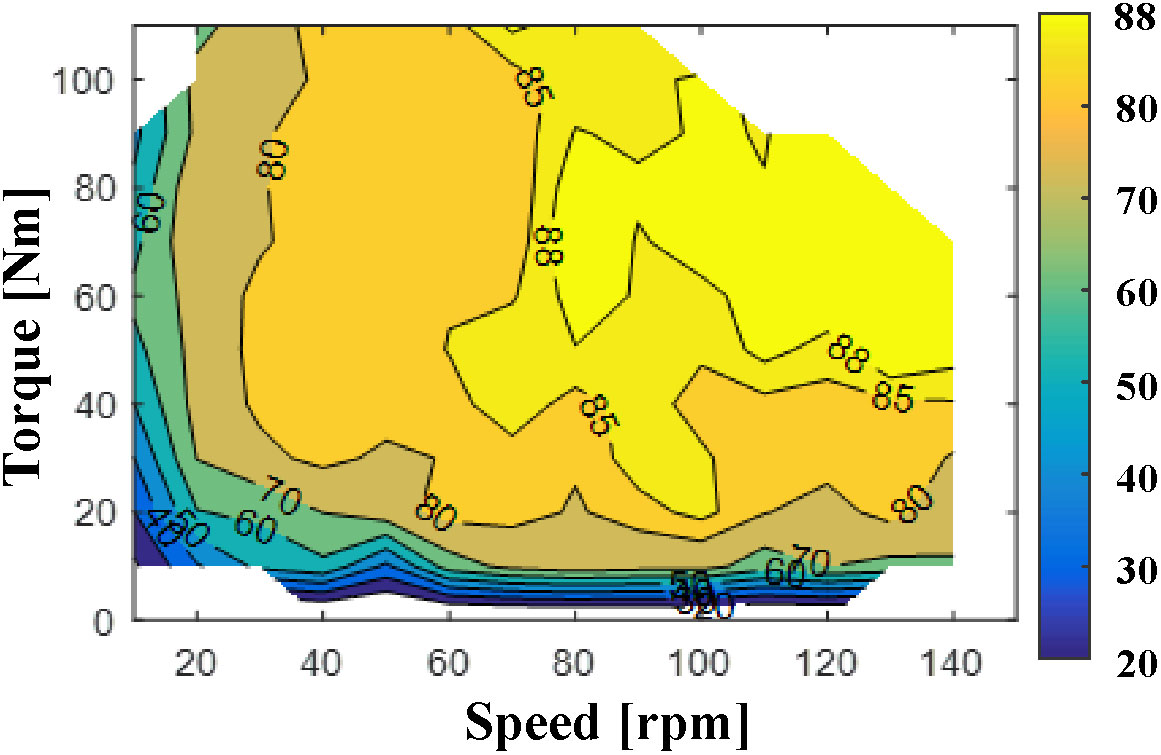
样机的效率图也经过测试，结果如图23所示。转速范围为0到142.5转/分钟，每10转/分钟记录一次数据。从效率图可以看出，所提出的电机在该转速下具有较大部分的效率高于80%，相对较高。当转速较低（小于20转/分钟）时，效率较低；当负载转矩较小时（小于30 N·cm），效率也较低。

转子铁芯。(b) 定子铁芯。(c) 定子组件。(d) 样机。)

样机的线反电动势。(b) 样机的THD值。)

95转/分钟。(b) 142.5转/分钟。)

六、结论

本文提出了一种为电动自动导引车设计的新型紧凑型双永磁可变磁阻电机（DPMVM）。该电机基于磁齿轮效应工作，采用带有两个分体齿和集中绕组的定子。文中对该DPMVM的工作原理进行了理论分析，并得出了槽/极选择指南。比较了相同定子槽数下不同转子极数的方案，选取效率和永磁体利用率较高的方案进行进一步优化。研究了主要尺寸参数对效率和转矩脉动的影响，发现较小的定子槽有助于提高所提出电机的效率并降低转矩脉动。转矩分解分析表明，仅由定子永磁体或仅由转子永磁体产生的总输出转矩高于两部分同时存在永磁体时的情况。制造了一台样机，并验证了所提出电机的性能。即使在低速（95转/分钟）下，该电机仍具有较高的效率。所提出电机的反电动势高度正弦化，总谐波畸变率非常低，且转矩脉动相对较低。通过分析与实验验证，该所提出电机非常适合用于电动自动导引车应用。