块量化：打破大模型部署的内存墙，通往高效推理的架构革命

最新推荐文章于 2025-12-12 14:20:45 发布

原创最新推荐文章于 2025-12-12 14:20:45 发布 · 1.6k 阅读

21 ·

CC 4.0 BY-SA版权

文章标签：

#架构 #大模型 #系统架构 #LLM #量化

AI大模型专栏收录该内容

175 篇文章

订阅专栏

近年来，大型语言模型在各项任务上取得了突破性进展，但其巨大的参数量也带来了严峻的部署挑战。一个拥有1750亿参数的模型，如果以标准的FP16（16位浮点数）精度存储，仅模型权重就需要消耗约350GB的显存。这远远超过了大多数商用GPU的承载能力，形成了所谓的“内存墙”。为了将这些“庞然大物”塞入有限的硬件资源中，模型量化技术应运而生，并成为大模型部署链条中不可或缺的一环。

量化，简而言之，是一种用低精度数据类型来表示高精度数据的技术。其核心思想是：牺牲微不足道的精度，换取巨大的存储空间和计算速度的提升。在量化技术的演进长河中，块量化的出现是一个重要的里程碑。它并非对传统量化方法的简单修补，而是一种架构层面的范式转移，巧妙地解决了传统方法在极低比特量化下的固有缺陷。

本文将作为一份技术指南，带你深入剖析块量化的架构设计。我们将从量化技术的基础讲起，揭示传统方法的痛点，详细阐述块量化的设计原理与优势，并通过生活化的案例和可执行的代码示例，让你彻底理解这一技术。最后，我们还将展望其未来的发展方向。（扩展阅读：SmoothQuant+：大语言模型4位量化技术的突破性进展、QLoRA技术深度解析：量化微调革命与大模型高效适配之道、4Bit NormalFloat量化技术：大模型高效部署的突破性创新、大模型瘦身术：剪枝、量化与蒸馏的技术博弈与创新设计）

量化基础与前Block时代的技术困境

在深入块量化之前，我们必须先理解标准量化的基本原理。

标准量化：从连续到离散的映射

量化的本质是一个信息压缩过程。它将连续的浮点数值映射到一个离散的、有限的整数集合上。这个过程通常分为两个步骤：缩放和零点偏移。

最常用的量化公式是仿射量化：

$X_{int} = \text{round}\left( \frac{X_{float}}{S} \right) + Z$

其反量化公式为：

$X_{float} \approx (X_{int} - Z) \times S$

其中：

$X_{float}$ 是原始的浮点数值。
$S$ 是缩放因子，一个浮点数，决定了量化的步长。
$Z$ 是零点，一个整数，用于确保实数0可以被精确表示。
$X_{int}$ 是量化后的整数值。

另一种常见的是对称量化，它假设数值分布关于零点对称，从而简化了计算（即 $Z=0$ ）：

$X_{int} = \text{round}\left( \frac{X_{float}}{S} \right)$

$X_{float} \approx X_{int} \times S$

关键点在于缩放因子 $S$ 的确定。它通常由待量化张量的数值范围决定。对于一个张量 $X$ ，其值域为 $\left [ \alpha,\beta \right ]$ ，目标整数范围为 $\left [ q_{min},q_{max} \right ]$ （例如，对于8比特，是[-128, 127]或[0, 255]），则：

$S = \frac{\beta - \alpha}{q_{max} - q_{min}}$

在标准量化中，这个“张量”的粒度通常是整个权重张量或一个输出通道。

传统量化的阿喀琉斯之踵：异常值与分布不均衡

标准量化在8比特及以上精度时表现良好。然而，当我们试图将其推向极致，使用4比特甚至2比特时，其根本性缺陷便暴露无遗。

问题根源：单一的缩放因子

标准量化为一个完整的张量（或通道）只计算一个缩放因子 S。这个 S 必须足够大，以覆盖张量中所有的数值，包括那些极其罕见的、绝对值巨大的异常值。

生活化案例：给一个班级的学生评分
想象一个班级，大部分学生的考试成绩在0到100分之间，但有一两个“天才”学生考了1000分。如果我们用标准量化的思路来“压缩”这个分数分布：

为了能表示0到1000分，我们必须将“缩放尺度”设得很大（比如，每1分代表10分）。
这样一来，对于占绝大多数的0-100分的学生，他们的分数在压缩后只有0-10个等级，分辨率极低。90分和100分可能被压缩成同一个等级，无法区分。
而那两个1000分的学生，虽然被精确表示了，但代价是牺牲了绝大多数普通学生的精度。

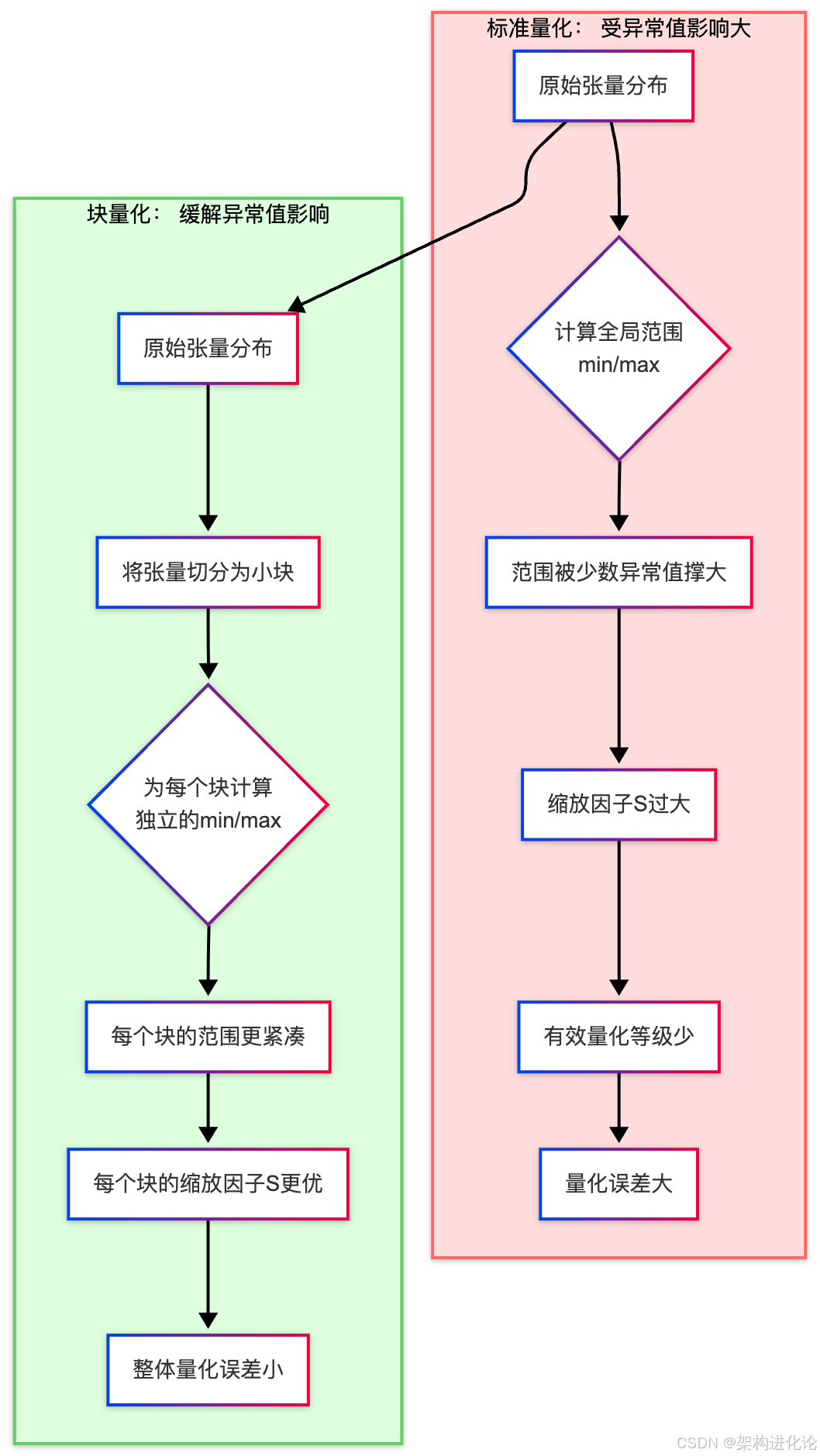
在神经网络中，这些“天才学生”就是异常值。研究表明，在大模型的权重和激活值中，异常值是普遍存在的。一个张量中只要存在极少数的极端异常值，就会“撑大”整个量化范围，导致用于表示绝大多数正常值的数值位被严重浪费，量化噪声急剧增大，最终导致模型精度崩溃。

下图清晰地展示了这一困境：

块量化：一种架构层面的范式转移

面对传统量化的困境，研究者们开始思考：为什么非要用一个尺度去衡量所有数据？能否为数据的不同部分“量身定制”更合适的尺度？这正是块量化核心思想的来源。

核心思想：分而治之，精细化缩放

块量化的核心创新在于改变了量化的粒度。它不再将整个张量或通道作为一个统一的量化单元，而是将其进一步细分为更小的、不重叠的“块”，然后为每一个块独立地计算缩放因子 S 和零点 Z。

这种“分而治之”的策略带来了立竿见影的好处：

局部适应性：每个块可以根据自身内部的数值分布来确定最合适的缩放因子，不再受其他块中异常值的“绑架”。
异常值隔离：即使某个块内存在异常值，其影响也被限制在该小块内部，不会污染整个张量的量化精度。
提升有效精度：由于每个块的范围更紧凑，缩放因子 S 更小，在相同的比特数下，每个块内用于表示数值的“等级”更多，从而显著降低了量化误差。

架构设计详解

块量化的架构设计主要包含三个关键维度：块形状、量化参数和计算流程。

1. 块形状的选择

块形状的选择是平衡计算效率与量化精度的关键。常见的块形状有：

一维块：(B, )，将张量展平后，每 B 个元素作为一个块。这是最常用的方式，实现简单。
二维块：(B1, B2)，适用于矩阵乘法的场景，可以与计算内核更好地结合。
通道维块：在卷积网络中，可以按通道方向分块。

在实践中，对于大型线性层的权重矩阵，通常将其展平后使用一维分块。块大小 B 是一个超参数，常见的值有64、128、256等。B 越小，量化越精细，但存储量化参数的开销也越大。

2. 量化参数的存储

在标准量化中，一个张量只需要存储一套 (S, Z)。而在块量化中，一个张量需要存储 N 套 (S_i, Z_i)，其中 $N = \frac{\text{total elements}}{B}$ 。

这引入了额外的元数据开销。对于一个大小为 M 的张量，量化到 b 比特：

数据体积： $M \times \frac{b}{8} \text{ bytes}$ 。
元数据体积： $\frac{M}{B} \times (\text{sizeof}(S) + \text{sizeof}(Z)) \text{ bytes}$ 。通常 S 和 Z 用FP16或FP32存储。

元数据开销与块大小 B 成反比。当 B 太小时，元数据开销可能变得不可忽视。因此，选择合适的 B 至关重要。

3. 计算流程

在推理时，使用块量化权重的矩阵乘法（MatMul）操作会变得更加复杂。以下是一个简化的计算流程图：

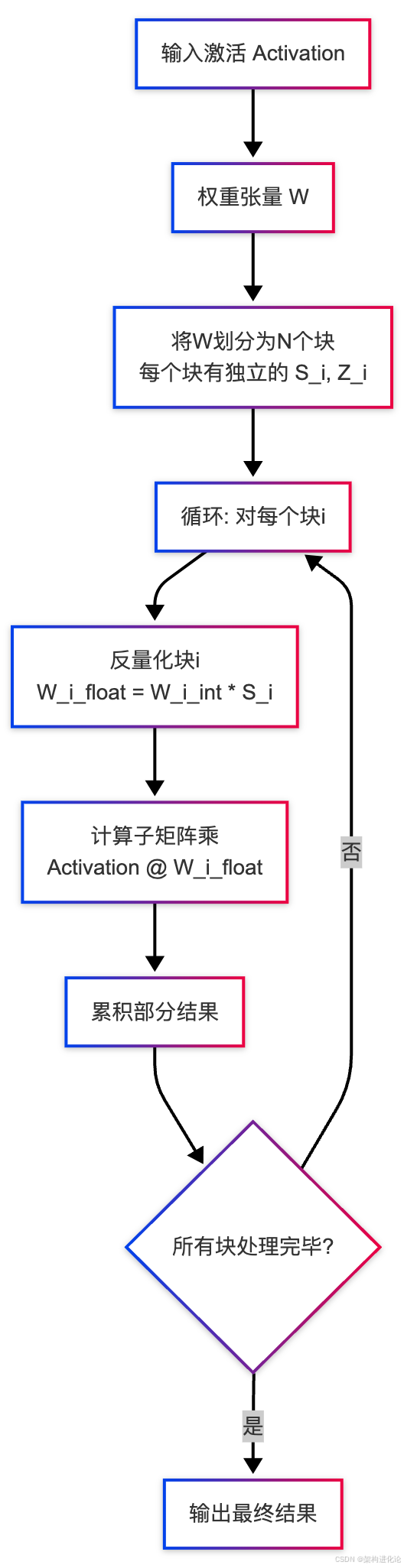
可以看到，标准的单次矩阵乘法被分解为一系列更小的矩阵乘法的累加。这个过程被称为反量化-计算循环。

块量化的优势与代价

优势：

突破极低比特量化瓶颈：这是其最主要的价值，使得4比特、2比特量化变得可行，模型压缩率提升4-8倍。
更高的精度保持：在相同的比特数下，块量化的精度显著高于标准量化。
灵活性：块大小是一个可调的超参数，可以根据模型结构和硬件特性进行优化。

代价：

计算开销：反量化操作需要在计算过程中动态进行，增加了额外的计算量。
元数据开销：需要存储额外的量化参数。
实现复杂性：需要定制化的内核来实现高效的“反量化-计算”融合操作，以避免频繁的内存读写。

从理论到实践：代码示例深度解析

理论总是抽象的，让我们通过一个完整的代码示例，亲手实现一个简单的块量化与反量化过程，并观察其效果。

import torch
import numpy as np
import matplotlib.pyplot as plt

def naive_block_quantize(tensor: torch.Tensor, bits: int, block_size: int):
    """
    实现一个朴素的块量化函数（对称量化）。

    Args:
        tensor: 待量化的FP32张量。
        bits: 目标量化比特数。
        block_size: 块大小。
    Returns:
        quantized_tensor: 量化后的INT张量。
        scales: 每个块的缩放因子。
    """
    # 0. 将输入张量展平为一维，便于分块处理
    original_shape = tensor.shape
    flattened = tensor.flatten()
    num_blocks = (flattened.numel() + block_size - 1) // block_size  # 计算总块数

    # 1. 初始化存储量化后数据和缩放因子的容器
    quantized_tensor = torch.zeros_like(flattened, dtype=torch.int32)
    scales = torch.zeros(num_blocks, dtype=torch.float32)

    # 2. 计算量化范围
    q_min = - (2 ** (bits - 1))  # 对于有符号整数，例如4比特: -8
    q_max = (2 ** (bits - 1)) - 1 # 对于有符号整数，例如4比特: 7

    # 3. 核心循环：对每个块进行独立量化
    for i in range(num_blocks):
        start_idx = i * block_size
        end_idx = min((i + 1) * block_size, flattened.numel())
        block = flattened[start_idx:end_idx]

        # 3.1 找到当前块内的绝对最大值，用于计算缩放因子
        abs_max = torch.max(torch.abs(block))
        # 防止除零，给一个极小值
        if abs_max == 0:
            abs_max = torch.tensor(1e-5)

        # 3.2 计算当前块的缩放因子 S
        # 公式: S = abs_max / q_max
        scale = abs_max / q_max
        scales[i] = scale

        # 3.3 量化：将浮点块缩放到整数范围并四舍五入
        # 公式: X_int = round(X_float / S)
        scaled_block = block / scale
        clamped_block = torch.clamp(scaled_block, q_min, q_max)
        quantized_block = torch.round(clamped_block).to(torch.int32)

        quantized_tensor[start_idx:end_idx] = quantized_block

    # 将量化后的张量和缩放因子恢复为原始形状（分块维度）
    quantized_tensor = quantized_tensor.reshape(original_shape)
    return quantized_tensor, scales

def naive_block_dequantize(quantized_tensor: torch.Tensor, scales: torch.Tensor, block_size: int, original_shape: tuple):
    """
    实现块反量化函数。

    Args:
        quantized_tensor: 量化后的INT张量。
        scales: 每个块的缩放因子。
        block_size: 块大小，必须与量化时一致。
        original_shape: 原始张量的形状。
    Returns:
        dequantized_tensor: 反量化后的FP32张量。
    """
    flattened_quantized = quantized_tensor.flatten()
    dequantized_tensor = torch.zeros_like(flattened_quantized, dtype=torch.float32)
    num_blocks = len(scales)

    # 反量化循环：对每个块进行独立反量化
    for i in range(num_blocks):
        start_idx = i * block_size
        end_idx = min((i + 1) * block_size, flattened_quantized.numel())
        quantized_block = flattened_quantized[start_idx:end_idx]
        scale = scales[i]

        # 反量化公式: X_float = X_int * S
        dequantized_block = quantized_block.float() * scale
        dequantized_tensor[start_idx:end_idx] = dequantized_block

    return dequantized_tensor.reshape(original_shape)

# === 演示与验证 ===
if __name__ == "__main__":
    # 1. 模拟一个包含异常值的权重张量
    torch.manual_seed(42)
    normal_weights = torch.randn(1000) * 0.1  # 大部分正常值
    outliers = torch.tensor([-2.5, 2.8])      # 少数异常值
    simulated_tensor = torch.cat([normal_weights, outliers])
    print(f"原始张量形状: {simulated_tensor.shape}")
    print(f"原始张量范围: [{simulated_tensor.min():.3f}, {simulated_tensor.max():.3f}]")

    # 2. 设置量化参数
    BITS = 4
    BLOCK_SIZE = 64  # 尝试改变这个值，观察效果

    # 3. 执行块量化
    quantized, scales = naive_block_quantize(simulated_tensor, bits=BITS, block_size=BLOCK_SIZE)
    print(f"量化后张量范围: [{quantized.min()}, {quantized.max()}]")
    print(f"缩放因子数量: {len(scales)}")

    # 4. 执行反量化
    dequantized = naive_block_dequantize(quantized, scales, BLOCK_SIZE, simulated_tensor.shape)

    # 5. 计算并比较误差
    quantization_error = torch.abs(simulated_tensor - dequantized)
    print(f"\n=== 量化误差分析 ({BITS}-bit, 块大小{BLOCK_SIZE}) ===")
    print(f"最大误差: {quantization_error.max():.4f}")
    print(f"平均误差: {quantization_error.mean():.4f}")
    print(f"均方根误差: {torch.sqrt(torch.mean(quantization_error**2)):.4f}")

    # 6. 对比标准量化（整个张量作为一个块）
    print(f"\n=== 对比: 标准量化（整个张量作为一个块）===")
    quantized_standard, scale_standard = naive_block_quantize(simulated_tensor, bits=BITS, block_size=simulated_tensor.numel())
    dequantized_standard = naive_block_dequantize(quantized_standard, scale_standard, simulated_tensor.numel(), simulated_tensor.shape)
    error_standard = torch.abs(simulated_tensor - dequantized_standard)
    print(f"标准量化 - 最大误差: {error_standard.max():.4f}")
    print(f"标准量化 - 平均误差: {error_standard.mean():.4f}")
    print(f"标准量化 - 均方根误差: {torch.sqrt(torch.mean(error_standard**2)):.4f}")

    # 7. 可视化结果
    plt.figure(figsize=(12, 6))

    plt.subplot(1, 2, 1)
    plt.hist(simulated_tensor.numpy(), bins=50, alpha=0.7, label='Original')
    plt.hist(dequantized.numpy(), bins=50, alpha=0.7, label=f'Block-Dequantized (B={BLOCK_SIZE})')
    plt.legend()
    plt.title("Value Distribution")
    plt.xlabel("Value")
    plt.ylabel("Frequency")

    plt.subplot(1, 2, 2)
    x = np.arange(len(simulated_tensor))
    plt.scatter(x, quantization_error.numpy(), s=10, alpha=0.5, label=f'Block Quant Error')
    plt.scatter(x, error_standard.numpy(), s=10, alpha=0.5, label='Standard Quant Error')
    plt.legend()
    plt.title("Quantization Error per Element")
    plt.xlabel("Element Index")
    plt.ylabel("Absolute Error")
    plt.yscale('log')  # 使用对数坐标更清晰地观察误差差异

    plt.tight_layout()
    plt.show()

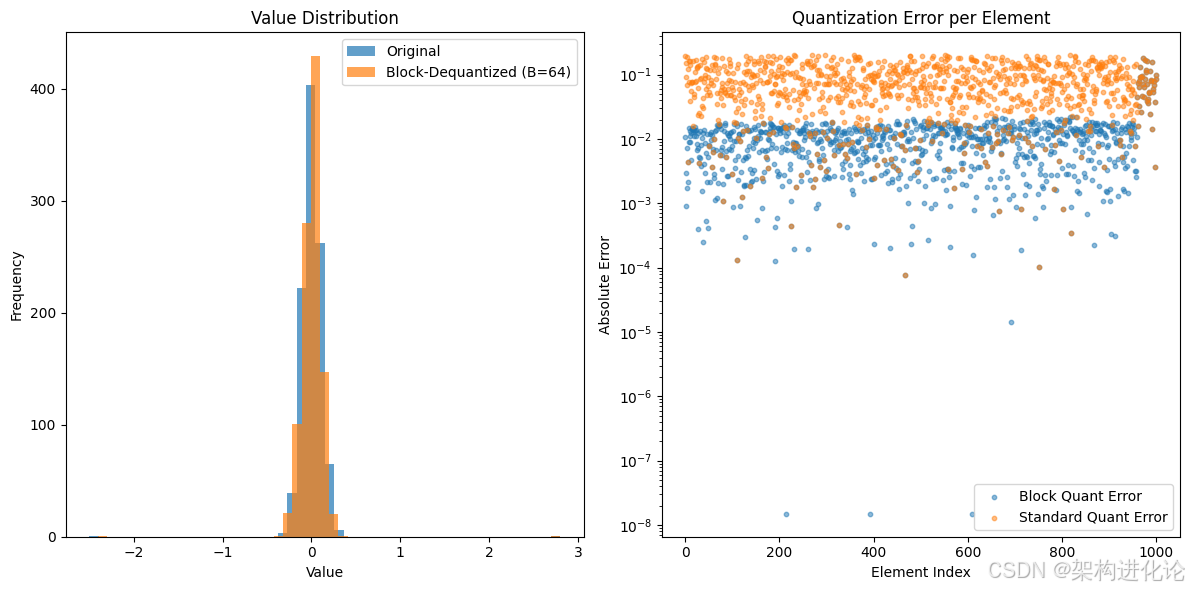
代码解读与运行结果分析：

模拟数据：我们创建了一个包含1000个正态分布值和2个明显异常值的张量，以模拟真实模型中的情况。

量化过程：naive_block_quantize 函数将张量展平后分块，对每个块独立计算缩放因子并进行量化。

反量化过程：naive_block_dequantize 函数根据存储的量化整数值和对应的缩放因子，恢复出浮点数。

误差对比：我们同时计算了块量化和标准量化的误差。

预期结果：块量化的各项误差指标（最大误差、平均误差、均方根误差）会显著低于标准量化。特别是最大误差，因为标准量化的缩放因子被异常值“撑大”，导致对正常值的量化步长过大，误差剧增。

可视化：通过直方图可以看到反量化后的数据分布与原始分布更为接近；通过散点图可以直观地看到，块量化的误差在整体上远低于标准量化。

你可以尝试修改代码中的 BITS（例如改为2或8）和 BLOCK_SIZE（例如改为16或256），观察不同参数下量化误差的变化，从而加深对块量化超参数影响的理解。

超越基础：块量化的高级变体与生态系统

基础的块量化已经带来了巨大的提升，但研究和工程上的优化并未止步。

量化数据类型：NF4与FP4

传统的量化将浮点数映射到均匀分布的整数上。然而，神经网络权重通常服从正态分布或拉普拉斯分布，这意味着数值在零点附近的概率密度更高。均匀分布的整数无法很好地匹配这种分布。

为此，一种名为正态浮点数4比特的数据类型被提出。NF4不是线性的，它的量化等级是非均匀的，在零点附近更密集，在分布的两端更稀疏。这更符合权重的实际分布，从而在相同的4比特下实现了更低的精度损失。

NF4-Levels = {−1.0,−0.696,−0.525,...,0.525,0.696,1.0}（具体的值由分位数决定）

双量化

块量化已经引入了元数据（缩放因子）的开销。为了进一步压缩，可以对缩放因子本身也进行量化，这就是双量化。

例如，首先对权重进行块量化，得到一组FP32的缩放因子 S。然后，再对这组 S 进行第二次量化（通常使用更高精度的量化，如8比特），得到 S_quantized 和 S_scale。在推理时，需要先反量化 S，然后再用它们去反量化权重。

虽然增加了步骤，但由于 S 的数据量远小于权重，对其量化可以带来净的存储收益。

与混合精度推理的结合

在实际部署中，并非所有层对量化都同样敏感。通常，模型的第一层和最后一层对精度更为敏感。因此，一个常见的策略是：

对模型中间的大部分层使用极低比特的块量化（如4比特）。
对输入、输出层和某些关键层保持更高的精度（如16比特或8比特）。

这种混合精度策略可以在保持整体高压缩率的同时，最大限度地减少精度损失。

总结与展望

块量化技术通过引入“分块”这一简单的架构思想，巧妙地解决了异常值对极低比特量化的干扰问题，为大模型的高效部署打开了新的空间。它将量化的粒度从“张量级”细化到“块级”，实现了更精细的数值表示，是模型压缩技术发展中的一个重要突破。

未来展望：

硬件友好型内核的成熟：目前，高效的块量化矩阵乘法需要定制的GPU内核来实现“反量化-计算”的融合，以隐藏反量化的延迟。未来，随着硬件厂商（如NVIDIA, AMD）和软件框架（如TensorRT, vLLM）对这类操作的原生支持，其运行效率将进一步提升。
自动化块大小与形状搜索：最优的块大小和形状可能因模型、层甚至输入数据而异。研究如何自动、高效地搜索这些超参数是一个有趣的方向。
与训练后量化及量化感知训练的深度融合：本文主要探讨的是训练后量化。将块量化的思想融入到量化感知训练中，让模型在训练阶段就适应块量化的噪声，有望在极低比特下实现更高的精度恢复。
更先进的数值表示：像NF4这样的非均匀数据类型将继续演进，以更好地匹配激活函数和权重的最新分布特性。

总而言之，块量化不仅仅是一种技术工具，它更代表了一种解决复杂问题的思维方式：通过引入适当的层次和结构，将全局性的难题分解为一系列可管理的局部问题。随着大模型技术的持续演进，这种“分而治之”的哲学思想必将在未来的模型架构和优化技术中扮演更加重要的角色。