先解释一下是怎么来到这里的(雾...学习Games101为解决走样问题需要对输入信号进行模糊化,这个过程要用到傅里叶变换,傅里叶变换的理解中又涉及欧拉公式(3B1B)。此外在unity学习四元数的时候也初见欧拉公式端倪(毕竟人家是欧拉角的替换方案),然而同济教材对欧拉方程描述一言难尽,我们学校直接跳过了傅里叶变换的部分,所以自学记录一下。借鉴了大量教程,只要我记得来源的都会标注在最下面。
complex number 复数
封闭性
如果对一个集合的成员进行运算 的成员总是产生该集合的成员,那么这个集合就是封闭的(Set is closed)
自然数(不包括0)在加法运算下是封闭的,但在减法运算下不是。 我们需要扩展自然数集,把 0 和负数包括进来才能使自然数集在减法运算下封闭。
整数是集合 Z = {...,-4,-3,-2,-1,0,1,2,3,4,...}。
整数在加法和减法运算下是封闭的。如果我们引入除法运算,就需要扩展我们的数系,将分数也包括在内。
有理数在加法、减法、乘法、除法中都是封闭的。 但幂和根不封闭。Real numbers are closed under addition, subtraction, multiplication and division, but not under power and roots.
在 R 中,方程 x2 = -1 没有解。我们可以从 R因此,我们发明了一个新的数,称为虚数imaginary numbers i。
实数加上虚数,就是最广泛的一类数: 复数。

模长:
共轭复数(complex conjugate)
辐角 Argument of a complex number & 辐角主值 principle value of the argument
注意其范围和表示
一定要画图,因为tanx的周期是Π,计算的辐角值+Π也能得到相同的tanb/a,所以要看图决定是否加Π(周期)
复数的3种表达方式
表示复数的方法有:
1.定义中的实数+虚数
2.复平面中通过向量的坐标表示
3.复平面中结合极坐标用三角函数表示


笛卡尔和极坐标表示的转化
从Cartesian到polar将三角函数的值算出即可

如果X/Y =0,画图就可知道角度,不用再计算了
如果用tan的方式计算从笛卡尔到极坐标的角度转换,先画图判断笛卡尔表示下复数在第几象限,因为tan的周期是Π,对于角度不同的角,结果是一样的,要根据实际角度,加减Π调整结果



当tan y(虚部)/x(实部)=0时,通过自己画图转化为极坐标表示。
如果题目给出复数的图像,也可以直接看图得出复数的polar form
运算
加减法

除法
笛卡尔表示:把除法换算成乘法做,在分子分母同时乘上分母的共轭。互为共轭的两个复数相乘是个实常数。这样做主要是在进行除法运算时,使分母变成一个实数,方便计算。

极坐标表示

乘法
定义表示: (a+bi)(c+di)=(ac-bd)+(bc+ad)i
极坐标表示:”模相乘,角相加“
证明:用到了两角和的余弦公式

一般形式:![]() 乘方
乘方
i 的乘法具有将矢量 z 逆时针旋转的几何效果。
z逆时针旋转 90 o 的几何效果 后面会有解释
De Moivre 公式(棣莫弗定理)
证明:欧拉公式
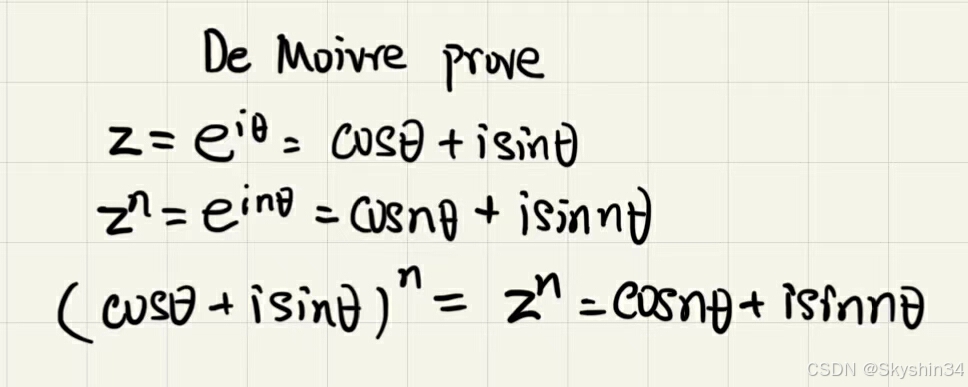
eg:
应用:求N倍角公式
复数高次幂应用德摩根公式(using De moivre's theorem) = 复数高次幂完全次方公式拆开的结果(expanding brackets),等式两侧根据实部和虚部系数相对应相等得到N倍角公式





复数根

eg1:计算含幂复数的根(root):De moivre
注意r大于0
复数转化为极坐标表示时注意tanx通过画图判断是否要加0
如果用Demovir通常是有幂,多少幂就有多少个根或者解,所以要在转化的那一步没进行任何操作时,给角度加2kΠ
eg2 求解复数方程:De moivre
1.等式两侧写为极坐标形式(你这提示我早悟出来了),高次幂复数应用德摩根公式展开
2.求r的特解,角度的通解(+2Π),每个解都小于2Π(因为大于2Π就与之前的解重合了)
3.求Z的通解




由于y/x = 0,看图即可知道角度

eg4.通解公式quadratic formula + 设欧拉解/ 凑平方complete the square求复数多于一项的复数方程的根
eg5.根据复数根的共轭性将一个根拓展到两个根,从而找到该方程的其他根Roots of Polynomials
因为我们这个因子一定是方程的解,所以余数一定为0即方程可以被解整除


eg6. 已知根找可能方程
eg7 Real zero 虚实零点

eg8 使方程满足解


求多项式相除余数remainder:Remainder Theorrm 多项式余式定理 / 长除法
Theorem意思是定理,Theory意思是理论
可以用长除法求
eg1:

eg2:

eg3:


2.欧拉公式
2.1 形式

这两个形式也被称为双曲函数,hyperbolic


2.2 验证(不是证明)
用泰勒展开去证明欧拉公式是错误的,由于在复数域中的泰勒级数展开、求导等运算均需要用到欧拉公式,造成循环论证,就好比你要证明1+1=2,于是先自顾自的规定了0.5+0.5 =1。但不失为一种验证方式:

验证 - 3B1B
i 的几何意义
想象一个复数Z = 0 + i ,在复平面中的坐标即为(0,1),此时我们从图像观察该复数的位置辐角是90°,模是1,用三角函数表示该复数:

此时再思考Z i ,此时模长没有变化,俯角增加90°(模相乘角相加)

至此我们赋予i在复平面单位圆中几何意义:不改变复数所代表的向量模长并逆时针旋转90°

重点:,该函数的随自变量变化的图像就是复平面的单位圆,是周期函数。而复平面单位圆可以用极坐标表示,两者联立起来,便可以得到欧拉公式
在复平面中复数z可用三角函数表示,cosθ^2 + sinθ^2 =1
因为e^iθ当θ =0°时r =1。而由上函数的变化率不改变函数值的大小,且由于变化率垂直于函数所以而e^iθ在复平面的函数图像也是一个半径为1的单位圆
因此两种表示Z的方式的范围是一样的,都是单位圆,因此可以相互等价。由此可建立等式


证明 - 泰勒公式



2.3 应用

例题:
定义->极坐标复数,通过欧拉公式转化为Exponenial指数复数

欧拉形式的复数转化为极坐标->定义复数
![]()

Hyperbolic and trigonometric functions 双曲和三角函数


eg:利用上面的结论证明三角恒等式对于双曲函数也成立

Osborne's Rule(奥斯本法则)

eg:

reference





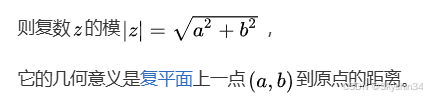














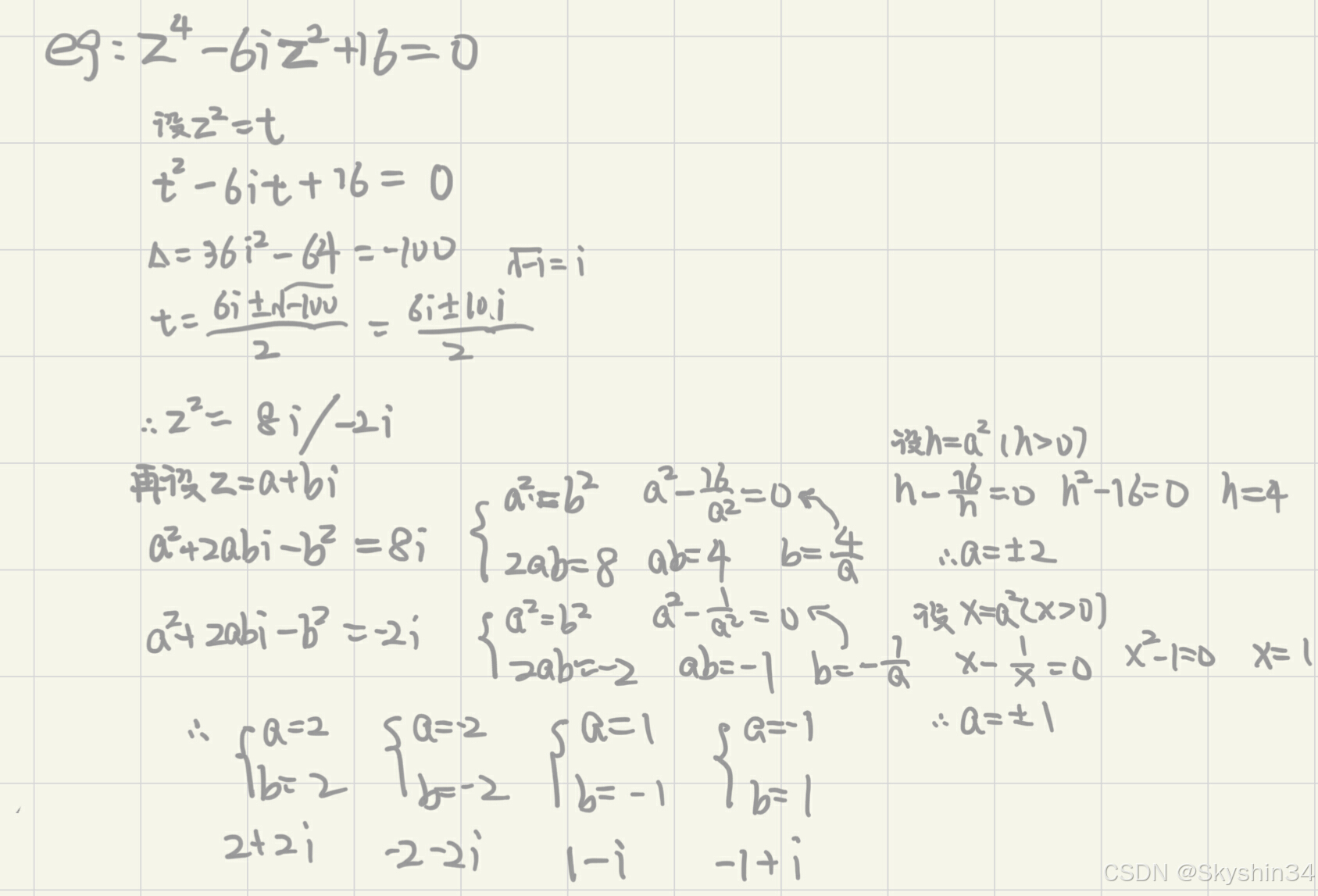



























 4290
4290

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








