In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted i i i, called the imaginary unit and satisfying the equation i 2 = − 1 i^2 = −1 i2=−1; every complex number can be expressed in the form a + b i a + bi a+bi, where a a a and b b b are real numbers. Because no real number satisfies the above equation, i i i was called an imaginary number by René Descartes. For the complex number a + b i a + bi a+bi, a a a is called the real part and b b b is called the imaginary part. The set of complex numbers is denoted by either of the symbols C {\displaystyle \mathbb {C} } C or C C C. Despite the historical nomenclature “imaginary”, complex numbers are regarded in the mathematical sciences as just as “real” as the real numbers and are fundamental in many aspects of the scientific description of the natural world.
Complex numbers allow solutions to all polynomial equations, even those that have no solutions in real numbers. More precisely, the fundamental theorem of algebra asserts that every non-constant polynomial equation with real or complex coefficients has a solution which is a complex number. For example, the equation ( x + 1 ) 2 = − 9 {\displaystyle (x+1)^{2}=-9} (x+1)2=−9 has no real solution, since the square of a real number cannot be negative, but has the two nonreal complex solutions − 1 + 3 i −1 + 3i −1+3i and − 1 − 3 i . −1 − 3i. −1−3i.
Addition, subtraction and multiplication of complex numbers can be naturally defined by using the rule i 2 = − 1 i^2 = −1 i2=−1 combined with the associative, commutative and distributive laws. Every nonzero complex number has a multiplicative inverse. This makes the complex numbers a field that has the real numbers as a subfield. The complex numbers also form a real vector space of dimension two, with { 1 , i } \{1, i\} {1,i} as a standard basis.
This standard basis makes the complex numbers a Cartesian plane, called the complex plane. This allows a geometric interpretation of the complex numbers and their operations, and conversely expressing in terms of complex numbers some geometric properties and constructions. For example, the real numbers form the real line which is identified to the horizontal axis of the complex plane. The complex numbers of absolute value one form the unit circle. The addition of a complex number is a translation in the complex plane, and the multiplication by a complex number is a similarity centered at the origin. The complex conjugation is the reflection symmetry with respect to the real axis. The complex absolute value is a Euclidean norm.
In summary, the complex numbers form a rich structure that is simultaneously an algebraically closed field, a commutative algebra over the reals, and a Euclidean vector space of dimension two.
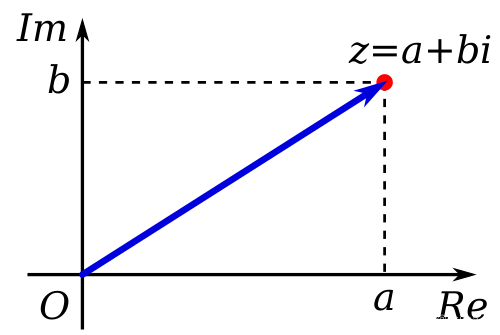
A complex number can be visually represented as a pair of numbers ( a , b ) (a, b) (a, b) forming a vector on a diagram called an Argand diagram, representing the complex plane. R e Re Re is the real axis, I m Im Im is the imaginary axis, and i i i is the “imaginary unit”, that satisfies i 2 = − 1. i^2 = −1. i2=−1.
Contents
1 Definition
A complex number is a number of the form a + b i a + bi a+bi, where a a a and b b b are real numbers, and i i i is an indeterminate satisfying i 2 = − 1 i^2 = −1 i2=−1. For example, 2 + 3 i 2 + 3i 2+3i is a complex number.
This way, a complex number is defined as a polynomial with real coefficients in the single indeterminate i i i, for which the relation i 2 + 1 = 0 i^2 + 1 = 0 i2+1=0 is imposed. Based on this definition, complex numbers can be added and multiplied, using the addition and multiplication for polynomials. The relation i 2 + 1 = 0 i^2 + 1 = 0 i2+1=0 induces the equalities i 4 k = 1 , i 4 k + 1 = i , i 4 k + 2 = − 1 , i^{4k} = 1, i^{4k+1} = i, i^{4k+2} = −1, i4k=1,i4k+1=i,i4k+2=−1, and i 4 k + 3 = − i i^{4k+3} = −i i4k+3=−i, which hold for all integers k k k; these allow the reduction of any polynomial that results from the addition and multiplication of complex numbers to a linear polynomial in i i i, again of the form a + b i a + bi a+bi with real coefficients a , b . a, b. a,b.
The real number a a a is called the real part of the complex number a + b i ; a + bi; a+bi; the real number b b b is called its imaginary part. To emphasize, the imaginary part does not include a factor i i i; that is, the imaginary part is b b b, not b i bi bi.
Formally, the complex numbers are defined as the quotient ring of the polynomial ring in the indeterminate i i i, by the ideal generated by the polynomial i 2 + 1 i^2 + 1 i2+1 (see below).
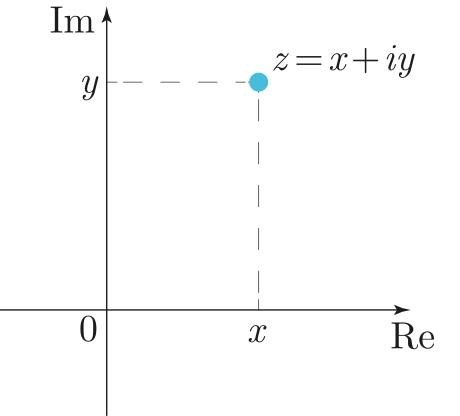
An illustration of the complex number z = x + i y z = x + iy z=x+iy on the complex plane. The real part is x x x, and its imaginary part is y y y.
2 Notation
A real number a a a can be regarded as a complex number a + 0 i a + 0i a+0i, whose imaginary part is 0 0 0. A purely imaginary number b i bi bi is a complex number 0 + b i 0 + bi 0+bi, whose real part is zero. As with polynomials, it is common to write a a a for a + 0 i a + 0i a+0i and b i bi bi for 0 + b i 0 + bi 0+bi. Moreover, when the imaginary part is negative, that is, b = − ∣ b ∣ < 0 b = −|b| < 0 b=−∣b∣<0, it is common to write a − ∣ b ∣ i a − |b|i a−∣b∣i instead of a + ( − ∣ b ∣ ) i a + (−|b|)i a+(−∣b∣)i; for example, for b = − 4 , 3 − 4 i b = −4, 3 − 4i b=−4,3−4i can be written instead of 3 + ( − 4 ) i . 3 + (−4)i. 3+(−4)i.
Since the multiplication of the indeterminate i i i and a real is commutative in polynomials with real coefficients, the polynomial a + b i a + bi a+bi may be written as a + i b a + ib a+ib. This is often expedient for imaginary parts denoted by expressions, for example, when b b b is a radical.
The real part of a complex number
z
z
z is denoted by
R
e
(
z
)
,
R
e
(
z
)
Re(z), {\displaystyle {\mathcal {Re}}(z)}
Re(z),Re(z), or
R
(
z
)
{\displaystyle {\mathfrak {R}}(z)}
R(z); the imaginary part of a complex number
z
z
z is denoted by
I
m
(
z
)
,
I
m
(
z
)
Im(z), {\displaystyle {\mathcal {Im}}(z)}
Im(z),Im(z), or
I
(
z
)
.
{\displaystyle {\mathfrak {I}}(z).}
I(z). For example,
Re
(
2
+
3
i
)
=
2
and
Im
(
2
+
3
i
)
=
3
.
{\displaystyle \operatorname {Re} (2+3i)=2\quad {\text{ and }}\quad \operatorname {Im} (2+3i)=3~.}
Re(2+3i)=2 and Im(2+3i)=3 .
The set of all complex numbers is denoted by C {\displaystyle \mathbb {C} } C (blackboard bold) or C C C (upright bold).
In some disciplines, particularly in electromagnetism and electrical engineering, j j j is used instead of i i i as i i i is frequently used to represent electric current. In these cases, complex numbers are written as a + b j , a + bj, a+bj, or a + j b . a + jb. a+jb.
3 Visualization
Main article: Complex plane
A complex number z z z can thus be identified with an ordered pair ( ℜ ( z ) , ℑ ( z ) ) {\displaystyle (\Re (z),\Im (z))} (ℜ(z),ℑ(z)) of real numbers, which in turn may be interpreted as coordinates of a point in a two-dimensional space. The most immediate space is the Euclidean plane with suitable coordinates, which is then called complex plane or Argand diagram, named after Jean-Robert Argand. Another prominent space on which the coordinates may be projected is the two-dimensional surface of a sphere, which is then called Riemann sphere.
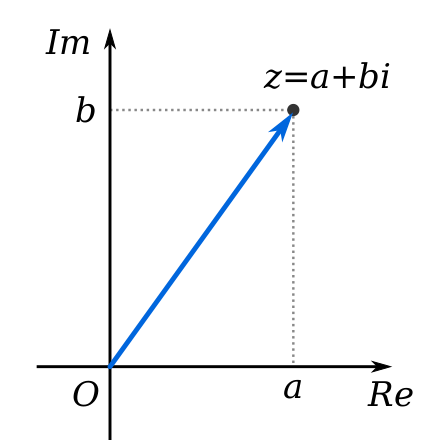
A complex number z z z, as a point (black) and its position vector (blue)
3.1 Cartesian complex plane
The definition of the complex numbers involving two arbitrary real values immediately suggests the use of Cartesian coordinates in the complex plane. The horizontal (real) axis is generally used to display the real part, with increasing values to the right, and the imaginary part marks the vertical (imaginary) axis, with increasing values upwards.
A charted number may be viewed either as the coordinatized point or as a position vector from the origin to this point. The coordinate values of a complex number z z z can hence be expressed in its Cartesian, rectangular, or algebraic form.
Notably, the operations of addition and multiplication take on a very natural geometric character, when complex numbers are viewed as position vectors: addition corresponds to vector addition, while multiplication (see below) corresponds to multiplying their magnitudes and adding the angles they make with the real axis. Viewed in this way, the multiplication of a complex number by
i
i
i corresponds to rotating the position vector counterclockwise by a quarter turn (90°) about the origin—a fact which can be expressed algebraically as follows:
(
a
+
b
i
)
⋅
i
=
a
i
+
b
(
i
)
2
=
−
b
+
a
i
.
{\displaystyle (a+bi)\cdot i=ai+b(i)^{2}=-b+ai.}
(a+bi)⋅i=ai+b(i)2=−b+ai.
3.2 Polar complex plane
Main article: Polar coordinate system
“Polar form” redirects here. For the higher-dimensional analogue, see Polar decomposition.
Modulus and argument
An alternative option for coordinates in the complex plane is the polar coordinate system that uses the distance of the point
z
z
z from the origin (
O
O
O), and the angle subtended between the positive real axis and the line segment
O
z
Oz
Oz in a counterclockwise sense. This leads to the polar form
z
=
r
e
i
φ
=
r
(
cos
φ
+
i
sin
φ
)
{\displaystyle z=re^{i\varphi }=r(\cos \varphi +i\sin \varphi )}
z=reiφ=r(cosφ+isinφ)
of a complex number, where
r
r
r is the absolute value of
z
z
z, and
φ
{\displaystyle \varphi }
φ is the argument of
z
z
z.
The absolute value (or modulus or magnitude) of a complex number
z
=
x
+
y
i
z = x + yi
z=x+yi is
r
=
∣
z
∣
=
x
2
+
y
2
.
{\displaystyle r=|z|={\sqrt {x^{2}+y^{2}}}.}
r=∣z∣=x2+y2.
If z z z is a real number (that is, if y = 0 y = 0 y=0), then r = ∣ x ∣ . r = |x|. r=∣x∣. That is, the absolute value of a real number equals its absolute value as a complex number.
By Pythagoras’ theorem, the absolute value of a complex number is the distance to the origin of the point representing the complex number in the complex plane.
The argument of
z
z
z (in many applications referred to as the “phase”
φ
φ
φ) is the angle of the radius
O
z
Oz
Oz with the positive real axis, and is written as
a
r
g
z
arg \ z
arg z. As with the modulus, the argument can be found from the rectangular form
x
+
y
i
x + yi
x+yi—by applying the inverse tangent to the quotient of imaginary-by-real parts. By using a half-angle identity, a single branch of the arctan suffices to cover the range
(
−
π
,
π
]
(−π, π]
(−π,π] of the
a
r
g
arg
arg-function, and avoids a more subtle case-by-case analysis
φ
=
arg
(
x
+
y
i
)
=
{
2
arctan
(
y
x
2
+
y
2
+
x
)
if
y
≠
0
or
x
>
0
,
π
if
x
<
0
and
y
=
0
,
undefined
if
x
=
0
and
y
=
0.
{\displaystyle \varphi =\arg(x+yi)={\begin{cases}2\arctan \left({\dfrac {y}{{\sqrt {x^{2}+y^{2}}}+x}}\right)&{\text{if }}y\neq 0{\text{ or }}x>0,\\\pi &{\text{if }}x<0{\text{ and }}y=0,\\{\text{undefined}}&{\text{if }}x=0{\text{ and }}y=0.\end{cases}}}
φ=arg(x+yi)=⎩
⎨
⎧2arctan(x2+y2+xy)πundefinedif y=0 or x>0,if x<0 and y=0,if x=0 and y=0.
Normally, as given above, the principal value in the interval ( − π , π ] (−π, π] (−π,π] is chosen. If the arg value is negative, values in the range ( − π , π ] (−π, π] (−π,π] or [ 0 , 2 π ) [0, 2π) [0,2π) can be obtained by adding 2 π 2π 2π. The value of φ φ φ is expressed in radians in this article. It can increase by any integer multiple of 2 π 2π 2π and still give the same angle, viewed as subtended by the rays of the positive real axis and from the origin through z z z. Hence, the arg function is sometimes considered as multivalued. The polar angle for the complex number 0 0 0 is indeterminate, but arbitrary choice of the polar angle 0 0 0 is common.
The value of
φ
φ
φ equals the result of atan2:
φ
=
atan2
(
Im
(
z
)
,
Re
(
z
)
)
.
{\displaystyle \varphi =\operatorname {atan2} \left(\operatorname {Im} (z),\operatorname {Re} (z)\right).}
φ=atan2(Im(z),Re(z)).
Together,
r
r
r and
φ
φ
φ give another way of representing complex numbers, the polar form, as the combination of modulus and argument fully specify the position of a point on the plane. Recovering the original rectangular co-ordinates from the polar form is done by the formula called trigonometric form
z
=
r
(
cos
φ
+
i
sin
φ
)
.
{\displaystyle z=r(\cos \varphi +i\sin \varphi ).}
z=r(cosφ+isinφ).
Using Euler’s formula this can be written as
z
=
r
e
i
φ
or
z
=
r
exp
i
φ
.
{\displaystyle z=re^{i\varphi }{\text{ \ \ \ \ \ or \ \ \ \ \ }}z=r\exp i\varphi .}
z=reiφ or z=rexpiφ.
Using the cis function, this is sometimes abbreviated to
z
=
r
c
i
s
φ
.
{\displaystyle z=r\operatorname {\mathrm {cis} } \varphi .}
z=rcisφ.
In angle notation, often used in electronics to represent a phasor with amplitude
r
r
r and phase
φ
φ
φ, it is written as
z
=
r
∠
φ
.
{\displaystyle z=r\angle \varphi .}
z=r∠φ.
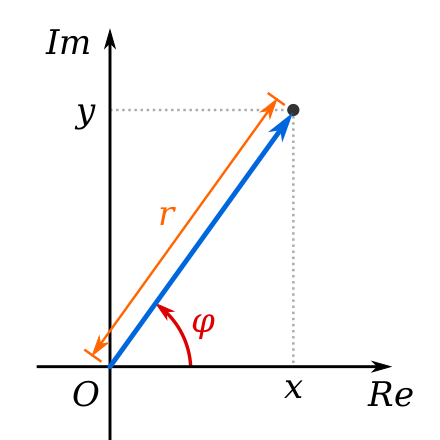
Argument φ and modulus r locate a point in the complex plane.
3.3 Complex graphs
Main article: Domain coloring
When visualizing complex functions, both a complex input and output are needed. Because each complex number is represented in two dimensions, visually graphing a complex function would require the perception of a four dimensional space, which is possible only in projections. Because of this, other ways of visualizing complex functions have been designed.
In domain coloring the output dimensions are represented by color and brightness, respectively. Each point in the complex plane as domain is ornated, typically with color representing the argument of the complex number, and brightness representing the magnitude. Dark spots mark moduli near zero, brighter spots are farther away from the origin, the gradation may be discontinuous, but is assumed as monotonous. The colors often vary in steps of π / 3 π/3 π/3 for 0 0 0 to 2 π 2π 2π from red, yellow, green, cyan, blue, to magenta. These plots are called color wheel graphs. This provides a simple way to visualize the functions without losing information. The picture shows zeros for ± 1 , ( 2 + i ) ±1, (2 + i) ±1,(2+i) and poles at ± − 2 − 2 i . {\displaystyle \pm {\sqrt {-2-2i}}.} ±−2−2i.
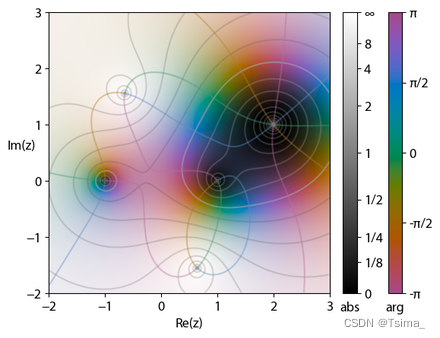
A color wheel graph of the expression
( z 2 − 1 ) ( z − 2 − i ) 2 z 2 + 2 + 2 i \frac{ (z^2 − 1)(z − 2 − i)^2}{z^2 + 2 + 2i} z2+2+2i(z2−1)(z−2−i)2






















 544
544

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








