Q学习在HEV能量管理中的适应性

基于Q学习的混合动力汽车监督控制适应性研究

摘要

作为自适应最优控制方法之一，基于Q学习的混合动力汽车(HEV)能量管理上层控制的适应性研究较为罕见。在实际驾驶场景中，车辆负载、道路条件和交通状况可能发生变化。如果这些变化发生而车辆监督控制未能适应，则可能导致燃油经济性无法达到最优。据我们所知，本研究首次对基于Q学习的混合动力汽车监督控制的适应性进行了探讨。本文针对三种变化工况——驾驶循环、车辆负载条件和道路坡度，对其适应性进行了全面分析。研究采用并联式HEV架构，并使用Q学习作为强化学习（RL）算法来控制发动机与电动机之间的扭矩分配。同时实现了模型预测控制、等效消耗最小化策略和恒温控制策略以进行对比。结果表明，基于Q学习的监督控制在不同条件下表现出较强的适应性，并且在所有三种变化工况下，其燃油经济性均优于四种监督控制中的其他方法。

索引词

强化学习，Q学习，监督控制，混合动力汽车，实时实现。

I. 引言

在混合动力汽车（HEV）的发展中，动力源之间的功率分配监督控制是一个主要挑战[1],[2]，文献表明，监督控制对燃油经济性有显著影响[3],[4]。它安排能量和功率流以协调电池使用、发动机使用、再生制动和动力辅助，这些都会影响车辆的燃油经济性[5]。在所有的混合动力汽车上层控制中，常用的方法包括基于规则的控制[6]、等效消耗最小化策略(ECMS)[7]、模型预测控制（MPC）[8]、和动态规划（DP）[9]、模糊逻辑控制[10]。

基于规则的混合动力汽车监督控制实现了从专家知识中提取的规则。它在上述监督控制中所需的计算能力最少。然而，其规则并非通过优化获得[11]，因此仍有改进空间。模糊逻辑控制是基于规则的控制的一种扩展，通常包含模糊化器、规则和去模糊化器三层结构。文献[5]研究了一种基于模糊逻辑控制/遗传算法的自适应智能能量管理系统（AIEMS）。研究表明，在ADVISOR软件中的（联邦高速公路驾驶循环）FHDS驾驶循环下，与默认的基于规则的控制相比，燃油消耗最多减少了0.7L/100km。尽管遗传算法结合未来的车载计算机可实现实时运行，但在当前车辆的车载计算机上可能面临实施挑战。提出了一个区间二型模糊逻辑控制，在节油方面优于一般的模糊逻辑控制[4]。然而，其道路功率需求方法需要获取车辆前方的道路条件信息。

与基于规则的控制和模糊逻辑控制不同，等效消耗最小策略（ECMS）是一种基于优化的监督控制方法，可在每个时间步长优化燃油经济性，并能够实时实现。然而，其单步优化时域限制了燃油经济性性能，这促使了模型预测控制（MPC）的研究。MPC考虑未来多个时间步长，在有限时间域[12]内优化燃油经济性。随着优化时域中时间步长数量的增加，MPC所需的计算能力急剧上升，限制了其实时实现。为应对多步优化带来的高计算需求，MPC需要采用简化的车辆动力总成模型[13]。但由此带来的副作用是模型精度存在一定的不确定性[14]。此外，MPC获得的优化结果仅为局部最优。动态规划（DP）作为一类全局最优的监督控制方法[15]，能够在给定驾驶循环下生成最佳的燃油经济性基准[16],[17]。然而，其计算需求极高，几乎无法实时实现。尽管已有文献表明，可以通过机器学习从离线DP结果中提取规则，并将训练后的机器学习模型用于实时实现[18]，但这种方法并非直接优化，且可能丢失部分信息。

在训练过程中，强化学习（RL）监督控制具有较低的计算成本，因此有望克服动态规划（DP）[19]对高计算能力的需求。此外，其节油性能已在混合动力汽车应用中以动态规划（DP）为基准进行了广泛研究[16]。因此，本研究将重点研究可实时实现的强化学习监督控制。

适应性对于混合动力汽车监督控制非常重要，因为车辆售出后许多因素可能会发生变化，例如城市和高速公路驾驶条件、道路坡度以及车辆负载条件。在车辆开发过程中，监督控制标定可能考虑了广泛的工况，但标定后的控制策略在特定场景下未必最优。因此，有必要对混合动力汽车上层控制的适应性进行全面的研究和评估。

强化学习（RL）的灵感来源于人脑学习，即在特定环境中获取新技能的过程[19]。作为人类，我们每天都在不断变化和动态的环境中主动调整自身的行为和决策。类似于人脑，强化学习（RL）具备一定的适应能力，尽管其尚未达到人脑的同等水平[20]。

近年来，强化学习（RL）在混合动力汽车监督控制领域受到关注[21],[23]。它与动态规划（DP）共享贝尔曼方程[15]，但可实现实时控制。强化学习通过与实际车辆或车辆模型的交互，学习如何提高燃油经济性。RL会强化带来良好燃油经济性的功率分配比，同时惩罚导致不良燃油经济性的功率分配比。已有研究报道了针对并联式混合动力汽车的强化学习监督控制的参数化研究[24]，讨论了状态、动作选择与离散化、动作探索以及良好经验选择等问题。与发动机与电池二元监督控制相比，RL使燃油经济性提高了16.3%[25]。当考虑不同电池温度和健康状态时，RL相较于基于规则的监督控制还显示出5%的节油效果[22]。一项研究利用基于GPS的强化学习控制来提升燃油经济性[26]。尽管许多研究表明基于强化学习的监督控制器能够改善燃油经济性，但在混合动力汽车应用中，强化学习监督控制的适应性尚未得到充分研究。

近年来，Q学习是混合动力汽车监督控制领域中最流行的强化学习（RL）算法[27],[28],[30]，但其在该领域的适应性尚未得到充分研究。因此，本研究聚焦于Q学习控制。Q学习通常分为两种类型：基于表格的和基于近似的。每种类型各有优缺点。Sutton等指出，表格型求解方法是强化学习最简单的形式，适用于状态数量和动作变量较少的情况，此时值函数可以精确表示为数组或表格[19]。在表格型求解方法中，能够找到精确的最优值函数和最优策略。这与近似求解方法不同，后者只能得到近似的值函数和最优策略。然而，当状态和动作变量的数量较大时，近似求解方法更加高效，因为基于表格的方法会消耗较大的计算成本。在混合动力汽车能量管理系统应用中，目前尚无明确证据证明无论状态和动作变量的数量是多还是少。在本研究中，采用表格法作为求解方法，因为其计算成本低且易于理解。

本研究探讨了基于Q学习的监督控制在变化场景中的适应性。作为对比，还实现了基于规则、等效消耗最小策略（ECMS）和模型预测控制（MPC）的控制方法。本研究的主要贡献体现在两个方面：

(1) 为了评估上层控制（特别是Q学习）的适应性，考虑了三个变化因素，包括驾驶循环、车辆负载条件和道路坡度。这是首个专注于混合动力汽车领域中Q学习适应性的研究。

（2）利用车速、荷电状态（SOC）、扭矩需求、发动机转矩、电动机扭矩、发动机燃油消耗、强化学习状态‐动作函数和强化学习动作图等多种信息，对Q学习、模型预测控制（MPC）、基于规则的控制和ECMS监督控制进行了全面比较。据作者所知，这是首次尝试研究强化学习监督控制在混合动力汽车能量管理问题中的适应性。

本文的其余部分组织如下：第二节介绍了车辆动力总成系统模型，包括发动机、电动机、电池、变速器和车辆动力学。第三节介绍了混合动力汽车功率分配问题的问题描述及相应的控制方法，介绍了Q学习、模型预测控制、等效消耗最小策略和恒温式监督控制。第四节介绍了适应性研究的设置，包括用于测试强化学习监督控制适应能力的所有变化工况。第五节分析了四种监督控制在四种变化工况下的适应性。最后，本文以结论结束。

II. 混合动力汽车动力学建模

本节旨在为混合动力汽车推进系统提供数学模型、映射和重要参数。关于车辆推进系统仿真，存在逆向法和正向法[1]。逆向法假设驾驶员模型是完美的，因此总是能够满足驾驶循环参考速度，这在现实中并不成立[22]。相反，正向法不采用完美驾驶员模型的假设。功率需求按正向计算，即从驾驶员模型到车轮。它考虑了能量管理控制对速度跟踪的影响，更加贴近实际。由于逆向法计算速度快且无失败风险，通常用于车辆设计；而正向法则通常用于实时控制[32]。因此，本研究采用正向法。

车辆配置

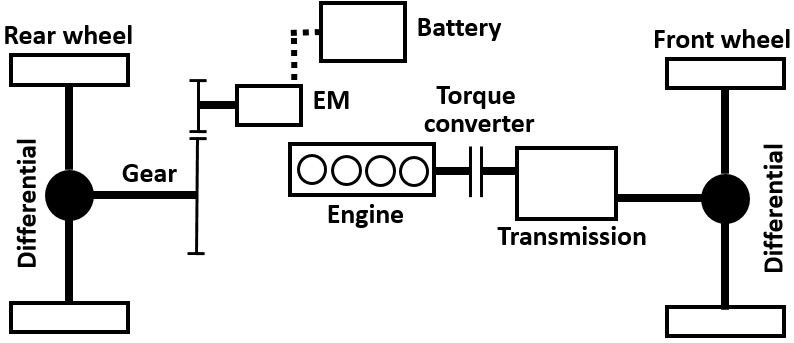
混合动力汽车的结构如图1所示。这是一种并联式混合动力汽车，其中电动机/发电机（EM）驱动后轮，发动机驱动前轮。电动机采用单级齿轮减速，而变速器具有四个档位。混合动力汽车的规格列于表I中。

表I 并联混合动力汽车规格

参数	数值
整车质量 (kg)	1500
车轮半径 (m)	0.33
主减速器传动比	3.5
变速器传动比 (1st-4th)	3.5, 2.0, 1.3, 1.0
发动机最大扭矩 (Nm)	115
电动机最大扭矩 (Nm)	400
电动机峰值功率 (kW)	50
电池类型	磷酸铁锂
电池容量 (Ah)	6.5
电池电压 (V)	300

电池SOC边界分别为10%和99%。单体电池的热管理通过被动风冷实现。初始单体电池温度设定为293K，环境温度也设定为293K。初始SOC设定为80%。

B. 建模

本节介绍了混合动力汽车模型，包括发动机、电动机、电池、变速器、驾驶员模型和车辆动力学。

1) 发动机 ：发动机燃油消耗率根据发动机转矩和发动机转速通过查表插值得到，如图2(a)所示。发动机转矩需求由监督控制确定。发动机转速由车速和变速器传动比决定。

2) 电动机/发电机 ：采用效率图对电动机进行建模，输入为电动机转速和电机扭矩，如图2(b)所示。与发动机模型的输入类似，电机扭矩来自监督控制，电动机转速则根据车速和电动机单级齿轮减速计算得出。

3) 电池 ：采用磷酸铁锂电池，单体电池容量为6.5安时。建立等效电路模型如下:

$$ U_{bat} = U_{oc} - I_{bat} R_{internal}. \quad (1) $$

$$ I_{bat} = \frac{P_{bat}}{U_{bat}} \quad (2) $$

其中，$U_{bat}$、$U_{oc}$分别为电池端电压和开路电压，$I_{bat}$为电池电流，$R_{internal}$为电池内阻，$P_{bat}$为电池输出功率。开路电压和内阻均被建模为电池SOC和温度的函数。

4) 变速器 ：变速器模型以先前的档位数、驾驶员需求和发动机转速为输入，以当前档位数为输出。例如，当先前的档位数为2时，当前档位数通过查找表确定，该查找表可在[24]中找到。

5) 驾驶员模型 ：驾驶员模型通过调节踏板位置来最小化车辆速度跟踪误差。采用前馈控制和反馈PI控制输出踏板位置[29]。前馈控制的输出如下:

$$ u_{ff} =
\begin{cases}
\frac{T_1}{T_{EM,max}}, & T_1 \geq 0, \
\frac{T_1 - T_{EM,min}}{(1 - \sigma) - \frac{H_{CG}}{m g r_{whl}}}, & T_1 < 0.
\end{cases} \quad (3) $$

$$ T_1 = \frac{\dot{v} {ref} J_v}{r {whl}} + r_{whl} \left( c_0 + c_1 v_{ref} + c_2 v_{ref}^2 \right) + m g \sin(\beta) \quad (3a) $$

其中$T_{EM,max}$和$T_{EM,min}$分别为电机最大和最小扭矩，$H_{CG}$为车辆质心高度，取500 mm，$m$为车辆整备质量，$g$为重力常数，$r_{whl}$为车轮半径，$B_w$为轴距，取2550 mm，$J_v$为车辆惯量，取150 kg·m²，$c_0,c_1,c_2$为道路阻力系数，分别取105.95、0.01和0.434，$\beta$为道路坡度。反馈PI控制输出计算如下:

$$ u_{fb} = k_p e_v(t) + k_i \int_0^t e_v(\tau) d\tau. \quad (4) $$

$$ e_v = v_{actual} - v_{ref} \quad (4a) $$

其中，$u_{fb}$为PI控制的输出，$e_v$为车辆速度误差，$k_p$和$k_i$分别为比例和积分增益，其值分别为0.5和0.01。整体驾驶员模型输出计算如下:

$$ u_{driver} = u_{ff} + u_{fb}. \quad (5) $$

$$ \theta_{acc} =
\begin{cases}
u_{driver}, & u_{driver} > 0 \
0, & u_{driver} \leq 0
\end{cases} \quad (5a) $$

$$ \theta_{brake} =
\begin{cases}
-u_{driver}, & u_{driver} < 0 \
0, & u_{driver} \geq 0
\end{cases} \quad (5b) $$

其中，$u_{fb}$是PI控制的输出，$e_v$是车辆速度误差，$\theta_{acc}$、$\theta_{brake}$分别为加速踏板和制动踏板位置，$k_p$、$k_i$为比例和积分增益，其值分别为0.5和0.01。根据$u_{driver}$的符号，仅加速踏板或制动踏板之一会主动执行$u_{driver}$的绝对值。

6) 车辆动力学 ：车辆加速力 $F_{acc}$ 是空气动力 $F_{air}$、滚动阻力 $F_{roll}$、坡度阻力 $F_{grade}$ 和牵引力 $F_{trac}$ 的综合结果，如下所示:

$$ F_{acc} = F_{air} + F_{roll} + F_{grade} + F_{trac}. \quad (6) $$

四个力的计算如下:

$$
\begin{cases}
F_{air} = 0.5\rho C_d A v_{veh}^2 \
F_{roll} = \cos(\beta) f_{roll} m g \
F_{grade} = \sin(\beta) m g \
F_{trac} = F_{ICE} + F_{EM}
\end{cases} \quad (7)
$$

其中，$\rho$为空气密度，$C_d$为空气阻力系数，$A$为车辆迎风面积，$v_{veh}$为车速，$f_{roll}$为道路滚动阻力系数，$m$为车辆整备质量，$g$为重力常数，$F_{ICE}$和$F_{EM}$分别为发动机和电机提供的牵引力。加速度力表达式如下:

$$ F_{acc} = m a. \quad (8) $$

$$ a = \dot{v}_{veh} \quad (8a) $$

其中$m$为车辆重量，$a$为车辆加速度，$v_{veh}$为车辆速度。发动机驱动力如下:

$$ F_{ICE} = \frac{T_{whl,front}}{r_{whl}}. \quad (9) $$

$$ T_{whl,front} = T_{trans,in} r_{fd} r_{gear} \eta_{trans}. \quad (9a) $$

$$ T_{trans,in} = T_{ICE}. \quad (9b) $$

电机驱动力计算如下:

$$ F_{EM} = \frac{T_{whl,rear}}{r_{whl}}. \quad (10) $$

$$ T_{whl,rear} = T_{EM} r_{EM} \eta_{EM,mech}. \quad (10a) $$

燃油消耗率根据燃油特性图进行插值得到，如下所示:

$$ \dot{m} {fuel,ICE} = f(\omega {ICE}, T_{ICE}). \quad (11) $$

$$ \omega_{ICE} = \frac{v_{veh}}{r_{whl} r_{fd} r_{gear}} \quad (11a) $$

其中，$r_{whl}$为车轮半径，适用于前轮和后轮。$r_{fd}$为主减速器传动比，$r_{gear}$为变速器传动比。电池输出功率如下:

$$ P_{bat} =
\begin{cases}
\frac{\omega_{EM} T_{EM}}{\eta_{EM,elec}}, & \text{dischg} \
\omega_{EM} T_{EM} \eta_{EM,elec}, & \text{chg}.
\end{cases} \quad (12) $$

$$ \eta_{EM,elec} = f(\omega_{EM}, T_{EM}). \quad (12a) $$

$$ \omega_{EM} = \omega_{whl,rear} r_{EM}. \quad (12b) $$

$$ \omega_{whl,rear} = \frac{v_{veh}}{r_{whl}} \quad (12c) $$

其中，电磁效率图如图2(b)所示。整车扭矩需求由驾驶员指令确定，并分配为内燃机和电机扭矩需求，具体如下:

$$ T_{dmd} = \theta_{acc} T_{ref} = T_{dmd, ICE} + T_{dmd,EM}. \quad (13) $$

总电机扭矩需求包括由 supervisory control 分配的扭矩需求和制动扭矩需求:

$$ T_{dmd,EM,total} = T_{dmd,EM} + \theta_{brake} T_{EM,min}. \quad (14) $$

III. 监督控制

本节介绍问题描述和上层控制，其中包括Q学习、模型预测控制、等效消耗最小策略和恒温式控制。混合动力汽车上层控制的目标是节约燃油，成本函数如下所示:

$$ J = \int_t^{t+T} \left( \frac{\dot{m} {fuel}(\tau)}{\dot{m} {fuel,norm}} + \frac{e^2_{SOC}(\tau)}{e^2_{SOC,norm}} \right) d\tau \quad (15) $$

其中，$t$为当前时间，$T$为成本函数计算的持续时间，$\dot{m} {fuel}$为燃油消耗率，$e {SOC}$为电池SOC调节项。$\dot{m} {fuel,norm}$固定为0.001kg/s，$e^2 {SOC,norm}$固定为0.01。$\dot{m}_{fuel}$不仅考虑发动机的燃油消耗率，还集成了电池的使用情况。驾驶员扭矩需求将由发动机和电机共同满足。控制策略决定发动机与电机之间的扭矩分配，因此不会与驾驶员的扭矩需求产生冲突。电池充放电通过以下公式转换为等效燃油消耗（EFC）:

$$ \dot{m} {fuel,bat} = \frac{c S {dis}}{\eta_{dis}} + \frac{(1 - c) S_{chg}}{\eta_{chg}} \cdot \frac{P_{bat}}{Q_{LHV} V}. \quad (16) $$

$$ c =
\begin{cases}
1, & \text{dischg} \
0, & \text{chg}
\end{cases} \quad (16a) $$

其中$c$为电池充放电状态，$S$为电池放电与充电等效因子，$\eta$为充放电效率，$P_{bat}$是电池放电/充电功率，$Q_{LHV}$是发动机燃油的低热值。$\dot{m}_{fuel}$是发动机燃油消耗和电池等效燃料消耗的总和:

$$ \dot{m} {fuel} = \dot{m} {fuel,ICE} + \dot{m}_{fuel,bat}. \quad (17) $$

电池SOC调节项目标是将SOC恢复至初始值。其定义如下:

$$ e_{SOC} =
\begin{cases}
SOC - SOC(0), & SOC \leq SOC(0) \
0, & SOC > SOC(0).
\end{cases} \quad (18) $$

监督控制的约束包括电池SOC边界、发动机扭矩限制、电机扭矩限制和电池功率限制。它们如下所示:

$$
\begin{cases}
0.1 \leq SOC \leq 0.99 \
0 \text{Nm} \leq T_{ICE} \leq 115 \text{Nm} \
-400 \text{Nm} \leq T_{EM} \leq 400 \text{Nm} \
-50 \text{kW} \leq P_{bat} \leq 50 \text{kW}.
\end{cases} \quad (19)
$$

A. Q学习

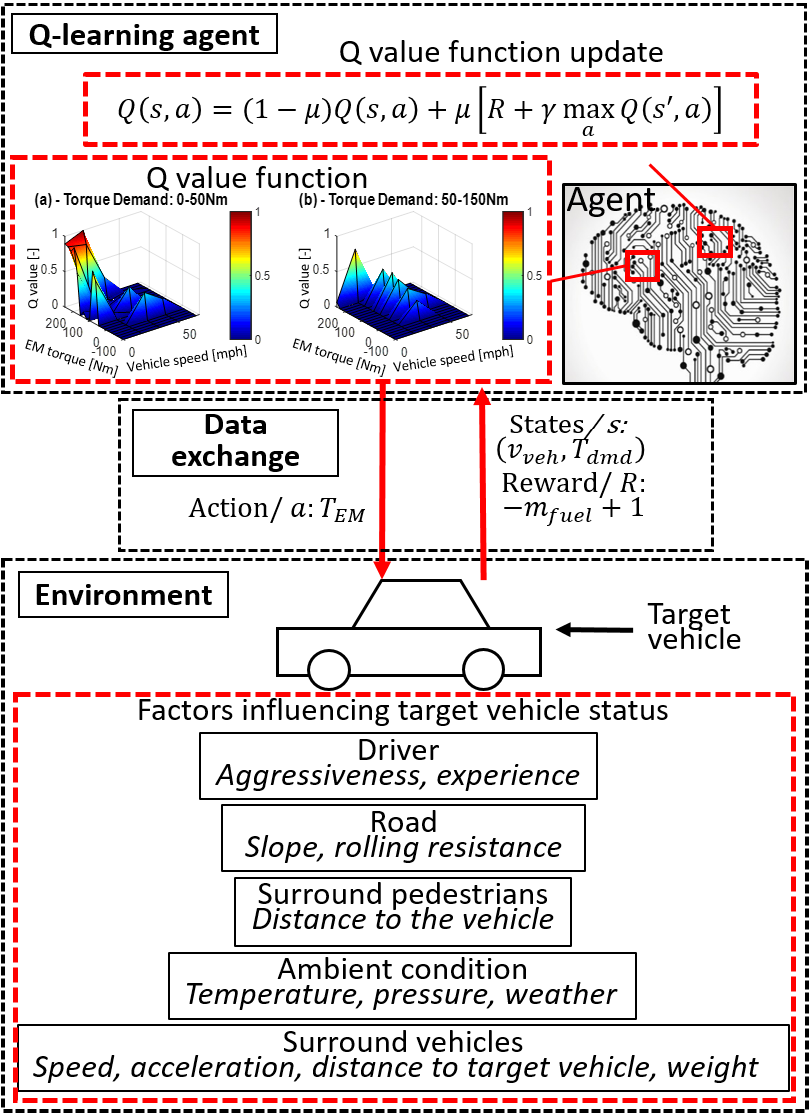
图3展示了混合动力汽车监督控制应用中的通用强化学习框架。该框架包含一个强化学习智能体和一个环境。智能体的目标是通过与环境的交互学习，以最大化奖励。

Q值更新方程如下:

$$ Q(s, a) = Q(s, a) + \alpha \left[ R + \gamma \max_{a’} Q(s’, a’) - Q(s, a) \right] \quad (20) $$

其中，$\alpha$是学习率，$R$是奖励，$s$是当前时间步长的状态，$s’$是下一个时间步长的状态，$\gamma$是折扣因子。本研究中学习率$\alpha$固定为0.05，折扣因子$\gamma$固定为0.9。$\alpha$后面的括号内的项表示Q值的误差。表II给出了Q学习算法。Q值初始化为零。然后，经验探索尝试一些随机动作并生成新经验。经验评估对经验的质量进行评估，并提取经验用于Q学习值函数的更新。最后，经验评估标准更新根据最新信息选择最佳标准。

关于自适应特性，强化学习智能体在检测到燃油经济性发生显著变化时即开始学习。当最佳燃油经济性在200次迭代内不再提升时，学习过程终止。奖励定义在公式(21)，该奖励是通过修改成本函数(15)得到的。

$$ R = 1 - J. \quad (21) $$

车辆扭矩需求、车速（$T_{dmd}, v_{veh}, SOC$）被选为状态。每个状态变量被离散为5个值。状态向量（$T_{dmd}, v_{veh}, SOC$）的下限/上限分别为0牛米/400牛米、0英里/小时/90英里/小时和0.1/0.99。更多状态向量可在[30],[31]中找到。状态向量的选择应进行系统性研究，但这不是本研究的重点。有关状态选择的详细信息，读者可参考[24]。

表II 算法I

电机扭矩需求被选为动作。动作变量离散为20个值。动作的下限/上限为-100牛米/250牛米。动作探索采用ε-greedy方法，本研究中ε固定为2%。

B. 模型预测控制（MPC）

满足第二节B部分定义的车辆动力学，模型预测控制在5秒的预测时域内最小化式(15)中定义的成本函数J，且假设未来的车辆扭矩需求与当前值相同。电机扭矩需求为模型预测控制输入，车辆速度和电池SOC为模型预测控制状态。输入和状态的上下边界与Q学习中的相同。在不同的驾驶条件下，所有变化均反映在车辆扭矩需求和车速中，这些因素已被考虑在模型预测控制优化中。

等效消耗最小化策略(ECMS)

ECMS是一种基于实时优化的控制策略，用于优化瞬时电动机和发动机运行效率。ECMS等效燃油消耗按如下方式计算:

$$ \dot{m} {fuel,ECMS} = \dot{m} {fuel,ICE} + \dot{m} {fuel,bat} \left( 1 - \frac{x {SOC}^3}{2} \right). \quad (22) $$

$$ x_{SOC} = \frac{SOC - SOC(0)}{SOC_H - SOC_L}. \quad (22a) $$

发动机燃油消耗率 $\dot{m} {fuel,ICE}$通过(11)计算，电池等效燃油消耗率 $\dot{m} {fuel,bat}$通过(16)计算。在自适应特性方面，ECMS监督控制能够适应各种变化工况。变化的扭矩需求不会影响(16)中的等效因子。所有变化都将反映在车辆扭矩需求和车速中，这两者是ECMS监督控制的输入。

D. 恒温控制

恒温控制旨在通过根据SOC水平[31]分配功率分配来维持电池SOC在其初始水平。其表达式如下:

$$ T_{EM} = \max\left(-T_{EM,sat}, \min\left(T_{EM,sat}, T_{EM,sat} k (SOC - SOC(0))\right)\right) \quad (23) $$

其中$T_{EM,max}$为电机最大扭矩，$T_{EM,sat}$为饱和电机扭矩，$k$为电机扭矩斜率。

IV. 仿真设置

本研究考虑的变化工况包括高速公路和城市驾驶循环、驾驶员激进程度、车辆负载条件以及道路坡度。

对于高速公路和城市驾驶循环的变化，驾驶循环从高速工况（高速公路燃油经济性驾驶循环 – HWFET，图4(a)）切换到城市工况（城市底盘测功机驾驶工况 – UDDS，图4(b)）。

为了进行比较，还使用了三种常见的混合动力汽车上层控制（即MPC、ECMS和恒温控制）。ECMS的等效因子固定为1.15，该值通过粒子群优化方法在UDDS驾驶循环中进行了优化。

总迭代次数为5000次，场景变化发生在2500次迭代结束时。若最大总奖励在200次迭代内不再增加，则Q学习探索自动终止。

基于Q学习的混合动力汽车监督控制适应性研究

V. 结果

本节首先展示了四种监督控制在无变化工况下的 UDDS驾驶循环中的结果。然后分析了三种变化工况的结果，以说明Q学习自适应特性的优势。

A. Q学习与模型预测控制与等效消耗最小策略与恒温控制对比

恒温控制、等效消耗最小策略、模型预测控制和Q学习的燃油经济性分别为32.6MPGe、42.3MPGe、50.7MPGe和55.8MPGe。MPGe单位表示每加仑汽油当量英里数，通过加入电池能耗对油箱燃油的每加仑英里数进行调整。一加仑汽油相当于电池中的33.7千瓦时能源[33]。

UDDS前600秒的比较结果如图5所示。在车速下降场景中可以观察到再生制动现象。

车速跟踪，(b) 电池 SOC，(c) 电机扭矩输出，(d) 内燃机燃油流量，(e) 内燃机扭矩输出，以及(f) 内燃机燃油消耗)

在前200秒内，MPC和Q学习的电池SOC趋势一致，这两种控制策略的SOC变化较小。相比之下，恒温控制和等效消耗最小策略表现出较大的SOC波动，在200秒时间段内SOC几乎下降了20%。较大的SOC下降反映在图5(c)中50秒至120秒之间的较大电机扭矩上。在同一时期，MPC和Q学习更倾向于使用发动机，如图5(e)所示。在200秒时，MPC和Q学习的等效燃油消耗低于恒温控制和等效消耗最小策略，如图5(f)所示。在200秒至300秒之间，等效消耗最小策略与恒温控制的不同之处在于大量使用发动机。在300秒时，等效消耗最小策略的等效燃油消耗低于恒温控制，如图5(f)所示。300秒之后，所有控制策略下的电池SOC呈现出相似的变化趋势。

四种控制策略之间的累积奖励（21）比较如图6所示。Q学习在所有控制策略中处于领先。

B. 不同驾驶循环下的比较

所有监督控制的总奖励学习曲线如图7所示。当驾驶循环从HWFET切换到UDDS后，四种监督控制的总奖励均立即上升。随后，Q学习在56次迭代后在总奖励上开始领先，并在700次迭代后延长领先优势。该学习过程展示了Q学习对不同驾驶循环的适应能力。如图7(b)所示，恒温控制与其他三种控制之间的等效燃油消耗存在较大差距。综上所述，与恒温控制、等效消耗最小策略和模型预测控制相比，Q学习在5000次迭代中分别节省了46.9%、13.9%和1.1%的燃油。HWFET和UDDS的最终MPGe值如表III所示。

表III 燃油经济性汇总（单位：[MPGe]）

控制策略	HWFET	UDDS
恒温控制	48.2	32.6
ECMS	58.4	42.3
MPC	61.8	50.7
Q学习	63.1	55.8

图8中的最优动作图（即贪婪策略）是根据迭代不同阶段的Q值函数生成的。x轴为整车扭矩需求，对应于(11)，y轴为车速。图中不同颜色代表不同的电机扭矩水平，右侧的颜色条标示了扭矩大小。在未进行任何迭代之前，动作被初始化为零，因此在整个策略图中均采取零电机扭矩动作。经过2500次迭代后，动作图根据HWFET驾驶循环进行了优化，燃油经济性达到63.1MPGe。此时动作图在不同区域显示出不同的电机扭矩。例如，在右下角区域，电机扭矩较大。该区域车速较低且车辆扭矩需求较高，表示车辆处于低速加速状态，对应于图4(a)所示HWFET驾驶循环的初始加速阶段。此区域内较大的电机扭矩表明电机在低车速时辅助车辆加速。经过5000次迭代后，动作图适应了UDDS驾驶循环，更多区域填充了非零电机扭矩，如图8(c)所示。一个明显的变化出现在图8(c)的左下区域，该区域车速范围为0英里/小时‐20英里/小时，整车扭矩需求为50牛·米‐175牛·米范围内。比较如图4所示的HWFET和UDDS速度曲线，UDDS速度值大部分时间处于0英里/小时‐20英里/小时范围内，而HWFET仅在循环的开始和结束时进入该区域。因此，动作图谱左下角更新的电机扭矩与UDDS循环的频繁访问相匹配。

初始化后且迭代前，(b) 2500次迭代后且驾驶循环从 HWFET切换至UDDS前，(c) 5000次迭代后)

HWFET循环下的四种控制仿真结果如图9所示。在图9(a)中，四种控制的速度跟踪性能均表现良好。在图9(f)的766秒处，Q学习的等效燃油消耗最低，其次是模型预测控制、等效消耗最小策略和恒温控制。恒温控制分别在前300秒内优先使用电动机，导致电池SOC下降近40%，这与图9(b)中UDDS驾驶循环下的电池SOC趋势相似。ECMS在前300秒内对电池的使用略少。MPC和Q学习在此期间均轻微充电。前300秒内恒温控制产生的较大电机扭矩解释了图9(c)中SOC的急剧下降。从300秒到766秒，四种控制策略之间的等效燃油消耗（EFC）差异没有显著变化，除了Q学习和MPC在600秒时交换了领先位置。恒温控制由于没有任何优化过程，表现出最差的燃油经济性。ECMS在其优化过程中未考虑未来状态。尽管MPC克服了恒温控制和ECMS的缺点，但其预测时域仍受计算时间限制。Q学习利用贝尔曼方程并考虑长期未来回报，这是其实现优异燃油经济性表现的主要原因。

车速，(b) 电池SOC，(c) 电机扭矩输出，(d) 内燃机燃油流量，(e) 内燃机扭矩输出，以及(f) 发动机和电机等效燃料消耗)

C. 不同车辆负载条件下的对比

当车辆负载在2500秒时增加，燃油消耗也随之增加，因此总奖励如图10所示有所下降。在车辆重量变化后，Q学习大约需要600次迭代来适应新的重量，之后便在无需探索的情况下运行。经过自适应学习后，Q学习在四种监督控制中的总奖励表现最佳。在图10(b)中，与MPC、等效消耗最小策略和恒温控制相比，Q学习分别节省了4.6%、23.2%和61.9%的燃油。

总奖励，以及(b) 等效燃油消耗)

D. 不同道路坡度下的对比

在不同道路坡度下，四种监督控制的燃油经济性在图11中进行了比较。经过2500次迭代后，Q学习在1%的道路坡度下开始学习，并在约550次迭代内产生四种监督控制中最高的每加仑汽油当量英里数。在更高的道路坡度下，四种监督控制的燃油经济性均下降。

E. 验证

在实际车辆应用中，应考虑测量误差。因此，采用正态分布误差注入车速测量中以验证四种控制策略。在车速测量误差（均值为0，方差为0.4）条件下，重复进行HWFET和UDDS驾驶循环的仿真。图12显示了5000次迭代过程中的燃油经济性对比。如图所示，尽管测量误差使总奖励产生小幅波动，但并未改变四种控制策略的总奖励排名。综上所述，四种控制策略对车速测量误差具有鲁棒性。

VI. 结论

本研究探讨了基于Q学习的混合动力汽车监督控制的自适应特性。文中提供了一个包含发动机、电动机、电池和车辆动力学的混合动力汽车模型。本研究首次比较了Q学习、MPC、ECMS和恒温式监督控制的自适应特性。

Q学习在三种驾驶条件（包括驾驶循环、车辆重量和道路坡度）下表现出较强的适应能力。在所有场景中，Q学习相较于恒温控制、ECMS和MPC均实现了最优的燃油经济性。MPC的燃油经济性位居第二，其次为ECMS和恒温控制。因此，Q学习可作为混合动力汽车的控制方法，以提升燃油经济性并适应变化的运行条件。

在未来的研究所中，计划了几个研究方向以改进Q学习在混合动力汽车应用中的表现。本文所使用的Q学习的实验验证是未来研究计划中最重要的部分。尽管Q学习表现出较强的适应性，但在适应过程中学习时间较长。未来的研究将探讨在适应过程中减少学习时间的方法。此外，驾驶员行为和交通拥堵等更多时变参数将在后续工作中加以实现。