XOR仲裁PUF的不安全性

XOR仲裁PUF不安全性：承诺与现实之间的差距

乔治·T·贝克尔(B)
德国波鸿鲁尔大学霍斯特·格特信息技术安全研究所，德国波鸿 georg.becker@ruhr‐uni‐bochum.de

摘要

本文展示了针对商用基于PUF的RFID标签的首个真实世界克隆攻击。所研究的商用物理不可克隆函数仅需测量4次协议执行即可被攻击，耗时不到200毫秒。利用RFID智能卡模拟器，便可冒充（即“克隆”）该物理不可克隆功能。尽管攻击这些标签所使用的四路PUF可通过传统机器学习攻击实现，但我们证明，即使这些标签被配置为理论上安全的异或 PUF，仍然可以被攻击。我们通过一种新的基于可靠性的机器学习攻击实现了这一点，该方法采用分而治之方法来攻击异或PUF。这种新的分而治之方法使得随着异或门数量的增加，所需挑战与响应的数量仅呈线性增长。
这与当前最先进的异或PUF机器学习攻击形成鲜明对比，后者已被证明在挑战与响应需求上呈现指数增长。
因此，现在可以攻击此前被认为能够抵御机器学习攻击的异或PUF结构。由于异或仲裁器PUF是最流行且最具前景的电学强PUF设计之一，我们提出的基于可靠性的机器学习攻击使人怀疑在实际中是否能够实现安全且轻量的电子强物理不可克隆函数。

关键词 ：物理不可克隆函数 · Machine学习 · Real-world攻击 · XOR物理不可克隆函数

1 引言

物理不可克隆函数（PUF）自首次提出以来，已获得广泛的研究关注 2001[21]。
物理不可克隆函数利用每个物理对象内部固有的制造差异，使每个物理实例具有唯一的身份标识。尽管最初的提案基于光散射[21],，但同年Gassend等人提出了首个电学形式的PUF——仲裁器PUF等[8]。物理不可克隆函数具有一些独特特性，使其成为轻量级身份验证方案以及防伪解决方案中颇具吸引力的研究目标。此外，物理不可克隆函数作为安全密钥生成与存储机制也受到了广泛关注。其中一个关键特征是其“不可克隆性”，即不可能构建出两个具有相同特性的物理不可克隆功能实例。

c©国际密码学研究协会2015T.G¨uney su and H. Handschuh(Eds.):CHES 2015, LNCS 9293, pp . 535–555, 2015.DOI:10.1007/978-3-662-48324-4 27
本文档由funstory.ai的开源PDF翻译库BabelDOCv0.5.10(http://yadt.io)翻译，本仓库正在积极的建设当中，欢迎star和关注。

536 G.T.贝克尔

物理不可克隆函数通常分为两类：弱物理不可克隆函数和强物理不可克隆函数。强物理不可克隆函数可以通过指数级挑战数量进行查询，以获得指数级响应数量。它们可用于身份验证协议以及密钥生成与存储。而弱物理不可克隆函数的挑战空间非常有限，仅可用于密钥生成与存储。在实际应用中，物理不可克隆函数有两个主要缺点。一个缺点是物理不可克隆函数容易受到环境条件和噪声的影响，因此其响应不可靠。为了应对这种不可靠性，需要采用错误校正方法，或由所使用的物理不可克隆函数协议容忍部分错误的响应位。另一个主要缺点是现有的电子强物理不可克隆函数可以在软件中被模拟，且此类软件模型所需的参数可通过机器学习技术进行近似估计。仲裁器PUF尤其如此。已提出若干基于仲裁器PUF的构造方案，例如异或PUF[31]和前馈物理不可克隆函数[15]。它们的共同点在于引入了一些非线性特性，以增加机器学习攻击的难度。尽管对于少量异或门的情况可以使用机器学习攻击异或PUF，但普遍认为只要使用足够多的异或门，异或PUF就能抵御机器学习攻击[12,28,29]。
这使得异或PUF成为最有前景的强物理不可克隆函数设计之一。

物理不可克隆函数（PUF）已经走出科学研究实验室，进入了商业产品领域。
例如，恩智浦（NXP）和美高森美（Microsemi）在其部分产品中使用了基于物理不可克隆函数的密钥存储。但PUFs在商用产品中的应用不仅限于安全密钥存储。
目前还有基于物理不可克隆函数的RFID标签可供使用。这些极为轻量级的标签被宣传为存储标签的安全替代方案，并被提议作为药品和奢侈品的防伪解决方案。此外，它们还可用于访问控制和支付应用。本文将深入研究此类商用基于物理不可克隆函数的射频识别标签。我们证明，可以在测量时间低于一秒的情况下对这些 RFID标签实施机器学习攻击。随后，可以利用RFID智能卡模拟器“克隆”这些 RFID标签。
尽管这些标签中检查的物理不可克隆功能架构极弱，可以使用传统的机器学习攻击在几秒钟内攻破，但我们还表明，即使是被认为安全的物理不可克隆功能构造也可能受到攻击。我们通过使用一种新的基于可靠性的机器学习攻击实现了这一点。
这种新攻击随着异或门数量的增加而表现良好，因此增加异或门的数量无法抵御该攻击。

1.1 相关工作

在寻找不同的电学物理不可克隆函数方面已有大量研究。流行的弱物理不可克隆函数方案例如环形振荡器物理不可克隆函数[31],静态随机存取存储器物理不可克隆函数[9],基于灵敏放大器的物理不可克隆函数[10,23]或总线保持器物理不可克隆函数[30]。大多数强物理不可克隆功能设计是仲裁器PUF的变体，例如异或PUF[31],前馈物理不可克隆函数[15]或轻量级物理不可克隆函数[18]。与大量提出新物理不可克隆功能或讨论其在可靠性及唯一性方面性能的论文（例如[14,16,33]）相比，相关研究关注较少

承诺与现实之间的差距：论XOR53的不安全性 7
机器学习攻击。我们对物理不可克隆函数上机器学习攻击的大部分了解都基于 R¨uhrmair等人的2010年CCS论文[29]。在该论文中，R¨uhrmair等人表明，可以使用进化策略和基于逻辑回归的机器学习算法来攻击XORPUF、前馈 PUF和轻量级PUF。然而，他们的结果显示，建模一个XORPUF所需的挑战响应对（CRP）数量随着异或门数量的增加而指数级增长。因此，他们得出结论：如果使用足够多的异或门，XORPUF能够抵御这些机器学习攻击。他们的初步分析是在模拟数据上进行的，但随后通过专用集成电路的实际测量验证了结果 [26]。

除了寻找能够抵御机器学习攻击的物理不可克隆函数外，还提出了协议和系统级对策来对抗机器学习攻击。首个系统级对策是可控PUF[7]的概念。在受控PUF中，PUF响应不会被直接暴露，而是仅传输多个PUF响应的哈希值。
由于PUF本身不可靠，这类受控PUF也需要纠错机制。其他更轻量级的方案包括反向模糊提取器[13] 或纤细PUF协议[17,25]。不同方案及其安全性的良好综述可在[6]中找到。另一研究方向探讨了针对PUF的各种侧信道攻击，例如 [3,5,19,24,32]中所述。PUF也作为密码协议的构建模块受到关注，并提出了强物理不可克隆函数的形式化定义[1,4,20]。然而，有研究指出，大多数现有的PUF并不符合形式化的PUF模型[27]。

1.2 贡献与组织结构

本文的主要贡献可以总结如下：
1. 我们提出了首个针对商用强物理不可克隆功能基RFID标签的克隆攻击，揭示了强物理不可克隆函数在实际应用中承诺安全性和实际安全性之间的差距。所采用的四路PUF可通过机器学习进行攻击，测量时间少于200毫秒。随后可使用硬件成本低于25美元的RFID智能卡模拟器对PUF进行“克隆”。2.提出了一种新的基于可靠性的机器学习攻击方法，用于攻击异或PUF。即使参数此前被认为在计算上不可行被机器学习攻击的异或PUF，也无法抵御这种新型攻击。我们的结果表明，普遍认为攻击异或PUF所需的响应数量随异或门数量呈指数级增长这一假设是错误的。因此，无论使用何种参数，普通异或物理不可克隆函数均无法在实际中使用。
除了这些主要结果外，我们对RFID标签的分析还深入揭示了攻击者在实际中能够收集到多少挑战‐响应对。在许多设计的安全分析中，使用的挑战与响应少于一百万组。相比之下，基于PUF的RFID标签的测量结果表明，攻击者实际上很可能会收集到数十亿个响应。

538 G.T.贝克尔

本文提出的基于可靠性的机器学习攻击基于一种名为CMA‐ES的机器学习算法。该机器学习算法以及仲裁器PUF在背景部分进行了介绍。在第3节中详细讨论了目标商用基于PUF的RFID标签，而在第4节中讨论了对这些标签的克隆攻击。在第5节中介绍了针对XORPUF的新可靠性机器学习攻击。最后，在最后一节中讨论了这些攻击的影响。

2 背景

我们研究的PUF标签使用了n路PUF，这是仲裁器PUF的一种变体。在本节中，我们将首先介绍仲裁器PUF，并解释如何在C语言软件中对仲裁器PUF进行建模，然后说明如何使用机器学习来近似所需的参数。

2.1 仲裁器PUF

仲裁器PUF的示意图如图1所示。仲裁器PUF由顶部和底部信号组成，这两个信号通过 k个延迟阶段传输。每个延迟阶段包含两个具有相同布局的2位多路复用器（MUX），且这两个多路复用器均接收顶部和底部信号作为输入。由于两条路径的布局完全相同，因此预期引入的延迟也应相同。然而在实际中，由于工艺变化，多路复用器中的每个晶体管都具有略微不同的延迟特性。因此，顶部信号和底部信号所经历的多路复用器延迟各不相同。由于每块芯片的工艺变化不同，这些延迟差异对每块芯片而言都是唯一的。如果第 i级的挑战位 ci为 ‘1’，则多路复用器将交换顶部和底部信号；若为‘0’，则两个信号不进行交换。这样，竞争信号可以走不同的路径：n级仲裁器PUF共有 2n条不同的路径可供竞争信号选择。在PUF末端的仲裁器用于判断两个信号中哪一个更快到达，若顶部信号先到达，则仲裁器输出‘1’；若底部信号先到达，则输出‘0’。

为了提高仲裁器PUF对机器学习攻击的抵抗能力，有人提出在PUF设计中加入非线性元素。在PUF设计中增加非线性的最常用方法之一是异或PUF。在 n‐异或PUF中，芯片上集成了 n个仲裁器PUF。每个仲裁器

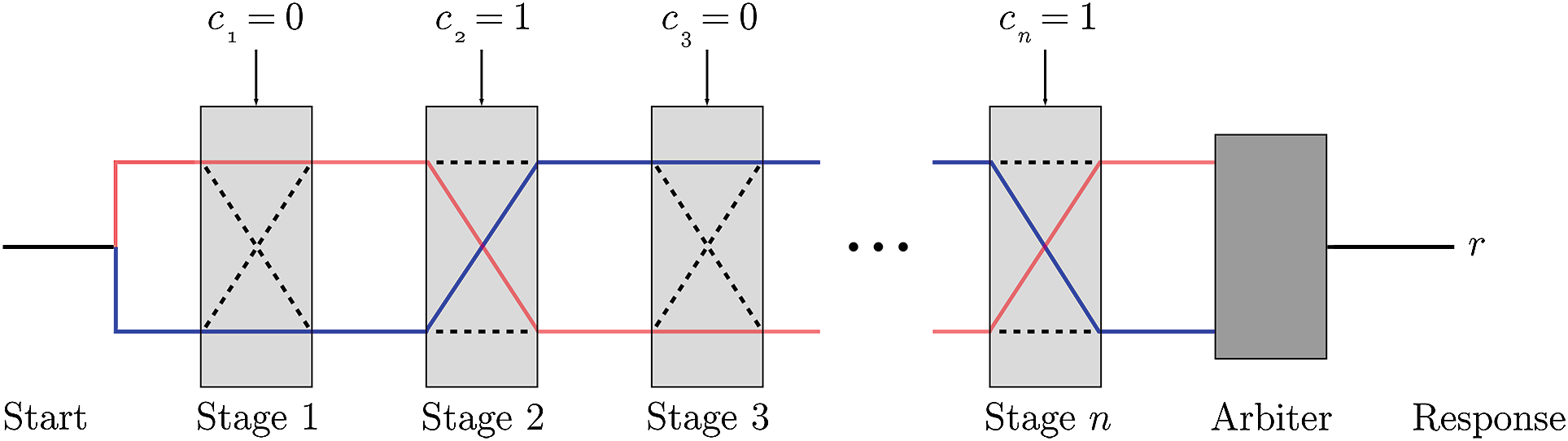
物理不可克隆函数接收相同的挑战， n个物理不可克隆函数的响应经过异或运算以生成最终响应位。虽然通过异或更多物理不可克隆函数可以提高机器学习抗性，但增加额外的PUF实例显然也会增加设计的面积开销。此外，异或的物理不可克隆函数越多，其可靠性越低。这限制了实际中可使用的异或门数量。
n级仲裁器PUF的响应由顶部和底部信号之间的延迟差异决定。该延迟差异是各个阶段延迟差异的总和。每个阶段的延迟差异取决于相应的挑战。因此，每级有两个延迟差异 i，即对应于挑战为‘1’时的延迟差异δ1,i 和对应于挑战为 ‘0’时的延迟差异δ0,i。对 k级仲裁器PUF进行建模的最有效方法是根据这些级间延迟差异计算一个延迟向量 w=(w1,…, wk+1)，具体如下：
w1= δ0,1 − δ1,1, (1a)
wi= δ0,i−1+ δ1,i−1+ δ0,i − δ1,i for 2 ≤ i ≤ k, (1b)
wk+1= δ0,k+ δ1,k (1c)
仲裁器末端的延迟差异 ΔD是转置延迟向量 w与从挑战 c导出的特征向量 Φ进行标量乘法的结果：
ΔD= wT Φ (2a)
r={1, ifΔD< 0. 0, ifΔD> 0.
(2b)
特征向量 Φ 从挑战向量 c中按如下方式导出：
Φi=
k
∏
l=i
(−1)cl for 1 ≤ i ≤ k (3a) Φk+1= 1 (3b)
过去已经表明，可以使用不同的机器学习技术高效地近似延迟向量 w。

2.2 进化策略

进化策略（ES）是一种广泛使用的机器学习技术，其灵感来源于进化理论。在进化过程中，物种通过自然选择（也称为适者生存）来适应环境变化。在每一代中，只有最适配的个体能够存活并繁殖，而较弱的个体则死亡，无法繁殖。由于下一代个体继承了上一代最适配个体的基因，因此物种得以持续改进。在基于进化策略的物理不可克隆函数机器学习攻击中，同样应用了适者生存的原则。如前所述，一个物理不可克隆功能实例

540 G.T.贝克尔

可以用其延迟向量 w来描述。对仲裁器PUF进行机器学习攻击的目标是找到一个延迟向量 w，使其最精确地逼近真实PUF实例。ES机器学习攻击的主要思想是生成随机PUF实例（即随机延迟向量 w），并检查哪些实例是最适配的，即哪些PUF实例最接近真实PUF模型。最适配的PUF实例将作为父代进入下一代，而其他PUF实例则被丢弃。在下一代中，通过父代的延迟向量以及一些随机变异（即对延迟向量的一些随机修改）生成子代。从这些子代实例中再次确定最适配的实例，并将其作为父代保留至下一代。该过程持续多代，使得PUF实例逐渐优化，越来越接近真实PUF的行为。

为了实施ES机器学习攻击，必须能够使用向量 w来描述一个PUF实例。此外，还需要一个适应度测试，该测试在给定延迟向量 w的情况下，能够确定哪些实例（即哪些延迟向量）是最适配的。由于仲裁器PUF可以使用延迟向量 w进行建模，因此ES机器学习攻击是否可行取决于是否存在适用于这些PUF模型的良好适应度测试。通常，针对仲裁器PUF所使用的适应度测试是物理PUF的测量响应 r与被测PUF实例的计算响应 r′之间的模型准确率。具有最高模型准确率的PUF实例被视为最适配的fittest。

存在许多ES机器学习算法的变体，这些变体主要区别在于每一代中保留多少父代、子代如何从父代生成以及随机突变如何被控制。通常，突变是通过向每个参数添加一个随机高斯变量 N(0, σ)来实现的。针对控制突变参数 σ，已提出多种方法。PUF实例越接近最优解， σ应越小。一种控制 σ的方法是在每一代中确定性地减小 σ。相比之下，在自适应中，突变参数会根据机器学习算法当前的表现自行调整。对于基于可靠性的机器学习攻击，采用[11]中建议的默认参数的协方差矩阵自适应（CMA）ES机器学习算法。CMA‐ES使用重组，即一个子代实例依赖于多个父代实例。它还使用自适应，即突变强度不是由确定性方式控制，而是根据ES算法的表现自行调整。

3 基于PUF的RFID标签

我们从一家RFID公司订购了基于PUF的RFID标签，该公司除了为我们主要订购的普通贴纸式标签外，还提供了四种不同格式的样品：智能卡格式、贴纸格式、腕带和抗金属标签。请注意，制造RFID标签的RFID公司与PUF集成电路的制造商不同。标签的照片以及所使用的射频识别读取器如图2所示。贴纸式标签可以使用

承诺与现实之间的差距：论XOR54的安全性问题 1

作为药品和奢侈品的防伪解决方案，在大批量订购时每个仅需几美分。RFID智能卡格式以及手环格式可用于访问控制、身份验证和支付应用。抗金属标签经过特殊设计，即使贴在金属表面也能正常工作，例如可放置于智能手机上。样品标签上的品牌名称表明，智能卡和手环标签是为支付和访问控制应用而设计的，而抗金属标签则印有忠诚度计划的品牌名称。

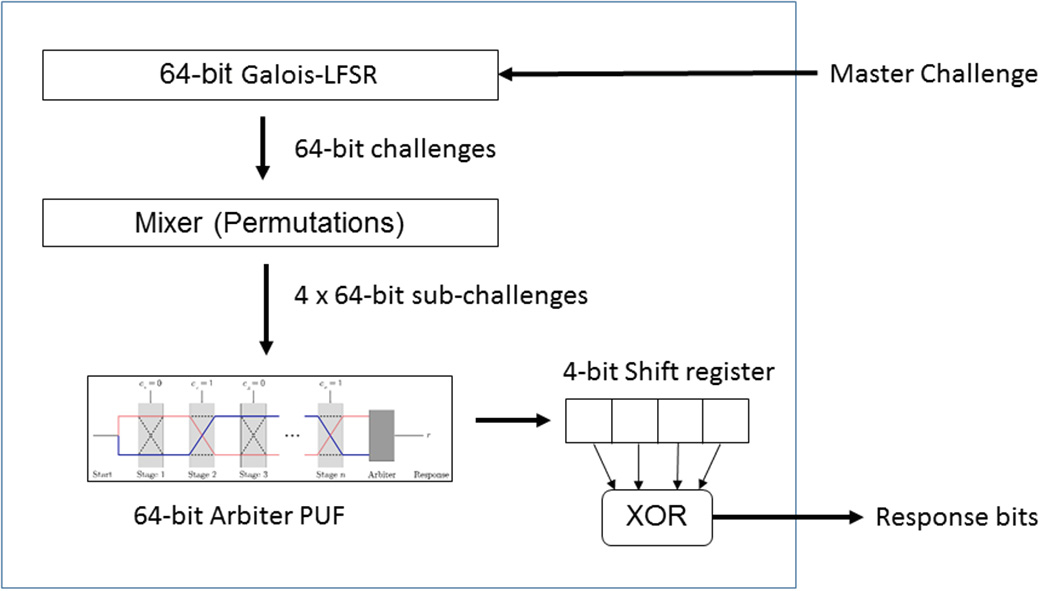
接下来将更详细地描述标签的架构。该架构是如何被逆向工程的，将在第 4节中详细说明。基于PUF的RFID标签的主要特性是，每个标签都可以基于内置的四路仲裁器PUF进行认证。所使用的四路PUF的结构如图3所示。读取器向标签发送一个64位主挑战。该主挑战被输入到一个64位线性反馈移位寄存器，以生成后续的挑战。每个64位挑战随后被输入到我们称为混合函数的模块。混合函数通过洗牌方式对提供的64位挑战进行处理，生成四个子挑战，其方式类似于轻量级物理不可克隆函数。这四个子挑战分别被输入到同一个64位仲裁器 PUF中。产生的四个响应位相互进行异或运算，形成一个单个响应位。这种使用单个仲裁器PUF并将 n响应位进行异或运算的PUF被称为n路PUF。在物理不可克隆函数协议中，每个64位主挑战生成256位响应。

传统上，仲裁器PUF的身份验证过程基于一个设置阶段，在该阶段中收集针对随机生成的挑战的响应，并将其存储在数据库中。在认证步骤期间，从该数据库中选择挑战并发送给标签。然后将被测标签的响应与数据库中存储的响应进行比较。如果响应匹配，则通过身份验证。然而，这种系统存在一些缺点。每个标签都需要维护一个庞大的挑战‐响应对数据库。如果标签用作一种

542 G.T.贝克尔

防伪解决方案，每个验证者都需要一个包含所有标签的挑战‐响应对的最新数据库。在实践中，这在大多数情况下需要互联网连接。
对于基于PUF的RFID标签，选择了一种允许离线认证的不同系统。该系统基于以下理念：如果已知仲裁器PUF的内部延迟参数，则可以在软件中对其建模。虽然这通常是一种不希望的特性，但它有助于构建无需预先收集的挑战‐响应对的PUF协议。在设置阶段，计算四路PUF的内部参数。我们不确定测试中的标签是如何精确实现这一步骤的，因为此步骤已由制造商完成。一种可能的解决方案是在设置阶段直接传输单个PUF响应，而不进行异或操作。仅需几百个这样的响应位，即可构建出PUF参数的精确模型。在建立PUF模型后，应禁用此阶段，以便仅传输混淆输出，即四路PUF的输出。
拥有这些延迟参数的验证者无需存储挑战‐响应对的数据库即可认证标签。
相反，任意挑战的响应可以在软件中实时计算得出。PUF参数的分发通过将参数以加密形式存储在标签上来实现。拥有对应密钥的合法验证者可以解密加密的延迟参数，并使用这些参数来验证标签。需要注意的是，加密的PUF参数仅在标签上进行存储，并不在标签上执行加密操作。因此，标签本身不需要加密功能和密钥。然而，这种方法也存在重大缺陷。验证者必须是可信实体，因为系统安全性依赖于密钥的保密性。这可能带来问题，且可信读取器需要达到最高标准。
承诺与现实之间的差距：论XOR543的不安全性 表1.基于PUF的RFID标签协议
物理攻击安全性。此外，验证者可以对物理不可克隆功能进行软件克隆，因此不再具备不可克隆性。因此，这样的系统不再提供物理不可克隆函数的关键特性之一，即不可克隆性。

4 攻击PUF标签

攻击PUF标签的第一步是逆向工程所使用的PUF设计，而我们对其细节并不了解。该射频识别公司向我们提供了一款用于测试标签的软件工具。该软件工具中使用的认证协议如表1所示。软件工具通过向PUF标签发送查询 auth来启动认证过程。PUF标签以其唯一标识符（UID）和加密的PUF参数进行响应。然后，该工具生成一个随机的主挑战 C并将其发送至标签。标签返回相应的响应字符串 r。该工具使用密钥 k解密加密的PUF延迟向量 w，并利用此延迟向量计算预期的响应字符串r′。如果接收到的响应字符串 r与计算出的响应字符串 r′之间的偏差低于阈值 τ，则PUF标签通过认证。该工具还支持一种以类似方式工作的“在线”验证。其区别在于，PUF参数的解密和响应计算由可信服务器执行，而非由软件工具本身完成。我们收到的标签已经过编程，并包含使用测试工具密钥加密的PUF参数。由于该软件工具也基于加密的PUF参数计算 PUF响应，这使得对PUF的逆向工程变得容易得多。无需进行硬件逆向工程，而是使用IDAPro对软件工具进行逆向分析。通过该逆向工程，我们得以推导出图3中已介绍的四路PUF的结构，包括所有参数，例如精确的线性反馈移位寄存器（LFSR）以及混合函数的详细信息。

544 G.T.贝克尔

4.1 机器学习攻击

为了收集攻击四路仲裁PUF所需的挑战‐响应对（CRPs），我们使用 MATLAB脚本向读取器发送随机挑战。一次完整的协议执行（包括发送一个 64位挑战并接收一个256位响应）大约耗时53毫秒。然而，可以通过在每次测量之间不发送新的主挑战来加快响应收集速度。若不发送新的主挑战，则前一次挑战的最后一个线性反馈移位寄存器（LFSR）状态将被用作新的主挑战。利用这一技巧，每次256位响应的测量时间可缩短至43毫秒。因此，在此设置下，每秒可收集超过5000个响应比特，每分钟可收集超过35万。我们希望强调，我们认为这些数字对于评估PUF在机器学习攻击下的安全性具有普遍参考价值。
在类似我们的设置下，攻击者收集数十亿个挑战‐响应对是完全合理的。
为了攻击PUF标签，我们测试了逻辑回归（LR）结合RProp的方法，如 [29]中所提出的，以及CMA‐ES机器学习算法。这两种算法均可用于攻击 PUF，但LR算法的性能远优于CMA‐ES算法。为了评估机器学习攻击，机器学习算法使用训练集来训练PUF参数，并使用另一个独立的集合——参考集，来评估生成的模型准确率。我们能够可靠地执行基于LR的机器学习攻击，仅需来自4次协议执行的数据作为训练集，即 4 · 256= 1024个挑战‐响应对，得到的平均模型准确率为85.8%。请注意，所达到的模型准确率非常接近观察到的 PUF标签平均可靠性87.5%，因此足以冒充该PUF。我们测试的10个不同标签均被成功攻击。测量1024个挑战‐响应对的时间仅为172毫秒，而在笔记本电脑上的平均计算时间约为40秒。当使用超过1024个挑战‐响应对时，计算时间实际上显著减少至几秒钟。
因此，这些基于PUF的RFID标签上采用的四路PUF无法提供针对机器学习攻击的任何保护，攻击者可以轻易恢复建模PUF所需的PUF参数。

4.2 克隆物理不可克隆功能标签

上一节中的机器学习攻击为我们提供了可用于构建物理不可克隆功能软件模型的参数。剩下的问题是，我们如何利用这些物理不可克隆功能参数来构建 PUF标签的克隆。为此，使用了可自由编程的RFIDsmartcard模拟器变色龙。该变色龙基于一个时钟频率为8兆赫兹的8位ATXmega32A4U微控制器，其外观如图2左侧所示。它的尺寸与标准智能卡相同，成本低于25美元，并且还有由小型电池供电的版本。变色龙是一个开源项目，有关变色龙的详细信息、P CB布局和固件可以在GitHub[22]上在线获取。变色龙的一个关键特性是能够设置唯一标识符，而这一点在大多数商用RFID卡和标签中是无法实现的。
承诺与现实之间的差距：论XOR545的安全性问题
我们在ATXmega上实现了基于PUF的RFID标签所使用的通信协议，以及四路 PUF的软件模型。PUF响应的计算具有时间关键性，因为如果PUF响应的计算耗时过长，将导致超时。为了加快PUF计算速度，我们仅对PUF延迟向量 w使用了5位精度整数，因为在8位系统中这种情况下不会发生溢出。该延迟向量是通过前一节所述的机器学习攻击计算得到的。
实现使用了C语言，在变色龙上计算一个128位响应块大约需要400,000个时钟周期，在32兆赫兹的时钟频率下，计算时间为12.8毫秒。在我们的实验中，这一速度足够快，不会触发任何超时。如前所述，我们为每个PUF仅使用了5位延迟参数，这降低了模型准确率，并导致变色龙的响应与演示工具计算出的响应之间出现约20%的偏差。平均约20%的偏差与软件工具计算出的响应和合法标签之间的偏差相似。该偏差远在软件工具可接受的错误率范围内。如果使用 16位精度数字，通过机器学习攻击推导出的参数实际上比加密的PUF参数具有更高的模型准确率。我们使用测试工具验证了此次攻击，软件将变色龙判定为合法PUF标签。这证明对这类基于PUF的RFID标签的克隆攻击在实践中是可行的。有趣的是，攻击者在实际中面临的最大挑战实际上是找到一种合适的可编程RFID芯片，以便自由设置其唯一标识符。然而，在缺乏可自由编程的 RFID智能卡的情况下，这一问题可以通过构建自己的RFID智能卡模拟器来简单解决。

5 基于可靠性的机器学习攻击

在上一节中，我们已经了解了如何攻击基于64级四路PUF的商用PUF标签。众所周知，小型异或PUF可以受到机器学习攻击，因此所使用的四向PUF能够被攻击并不令人意外。因此，在本节中，我们将更深入地研究更安全的架构。特别是，我们提出了一种新的基于可靠性的机器学习攻击方法，与来自[29]的机器学习攻击相比，该方法在增加的异或门数量增多时具有更好的可扩展性。在传统的机器学习攻击中，攻击者试图基于响应位的值来建模物理不可克隆函数。然而，不仅响应的值包含有用信息，响应的可靠性（即对于给定挑战，PUF产生相同响应位的频率）也包含有价值的信息。Delvaux等人首次指出了这一点 [5]。他们观察到，如果环境条件保持稳定，仲裁器PUF在特定挑战下的延迟差异与相应响应位的不可靠性成正比。这是因为各种噪声源会在延迟差异上添加一个近似高斯延迟 Dnoise= norm（μ， σ） ΔD。因此，当同时考虑噪声时， PUF模型的公式2将变为：

546 G.T.贝克尔

ΔD=ΔDP UF+ Dnoise= wT Φ+ Dnoise (4a)
r={1, ifΔDP UF+ Dnoise< 0. 0, ifΔDP UF+ Dnoise> 0.
(4b)
关键观察结果是，如果给定挑战Φ的延迟差异 ΔDP UF非常大，则噪声项 Dnoise改变ΔD符号的可能性很小。然而，如果延迟差异ΔDP UF接近零，则响应位因 Dnoise而发生变化的概率要高得多。Delvaux等利用单个响应位的确切可靠性值来近似该响应的延迟差异[5]。通过各个响应的确切延迟差异，可通过求解一组线性方程组来计算各个阶段的延迟。然而，Delvaux等指出，这种方法不如机器学习算法高效。此外，他们的方法无法应用于异或PUF，因为需要知道每个仲裁器PUF的单个响应位及其确切的可靠性。
G.T.贝克尔等拓展了利用不可靠性这一思路，并提出了一种基于机器学习[3]的故障攻击。改变环境条件（如温度或电源电压）具有与热噪声类似的效果，但通常更为显著。对受控PUF进行故障攻击的思路是：改变特定响应位的电源电压，并观察受控PUF的响应是否发生变化。该信息随后被用于基于 CMA‐ES的机器学习攻击。本文通过引入分而治之策略，扩展了该攻击的基本思想，从而获得了攻击XORPUF的能力。此外，本文并未通过改变电源电压来执行主动故障攻击，而是仅利用PUF固有的不可靠性。因此，测量可以在相同的环境条件下进行。借助这一新策略，我们能够攻破那些若仅关注输出位的传统机器学习算法将难以在计算上实现攻击的XORPUF。

5.1 基于可靠性的CMA‐ES攻击

基于可靠性的CMA‐ES攻击的核心思想是对同一挑战进行多次测量，以观察哪些响应位是稳定的，哪些响应位有时会发生翻转。如果某个挑战的响应不稳定，则对应的延迟差异 ΔDP UF很可能接近于零，即|ΔDP UF| < ε。但如果某个响应位对于给定挑战具有高可靠性，则延迟差异很可能较大，即|ΔDP UF| > ε。我们通过使用基于这一观察的适应度函数，对CMA‐ES机器学习算法进行了轻微修改。
该适应度函数的目标是测试一组给定的PUF模型 w中哪一个表现最佳，即哪个是最适配的。在第一个步骤中，将相同的挑战 Φi发送到PUF共 l次，以收集 l个响应位
ri,1, ri,2,..,ri,l。然后使用以下公式计算挑战 Φi的可靠性 hi：
承诺与现实之间的差距：论XOR547的不安全性
hi= | l 2 −
l
∑
j=1
ri,j| (5) 为了测试给定的PUF模型 w的适应度，攻击者首先通过检验相应的绝对延迟差 |ΔDi| 是否大于误差边界 ε，来计算所有挑战Φi的假设可靠性˜ hi：
h˜i={1, if|wT Φi| > ε
0, if|wT Φi| < ε
(6)
在下一步中，攻击者会检查假设可靠性向量˜ ˜ ˜h= h1,.., hn与测量的
可靠性向量 h= h1,.., hn的匹配程度。这是通过计算 h和 h之间的皮尔逊相关系数来实现的。相关系数反映了两个向量之间的线性关系。因此，它可用于测试PUF模型 w的假设可靠性向量 h与观测到的可靠性 h的匹配程度。相关系数越高，该PUF模型就越适合。对CMA‐ES算法的唯一其他修改是参数 ε成为一个需要由机器学习算法近似的额外参数。因此，对于一个 k级仲裁器 PUF，机器学习算法需要近似 k+ 2个而非 k+ 1个参数。除此之外，基于可靠性的CMA‐ES攻击的工作方式与传统CMA‐ES攻击相同：在每一代中生成多个PUF模型，并通过适应度测试对其进行评估。保留最优模型，并用它们生成下一代的PUF模型。通过这种方式，PUF模型在每一代中逐步改进。
该攻击首先使用从商用RFID标签的四路PUF中获取的挑战‐响应对进行测试。在四路PUF中，四个独立的响应位经过异或运算生成最终响应位。因此，由于攻击者无法获知给定PUF响应的可靠性，只能测量最终响应位的可靠性，所以需要调整适应度函数。第一步是计算四路PUF四个子挑战的可靠性值，然后将这四个子挑战的可靠性值简单相加。需要注意的是，预期不可靠的子挑战越多，测得的响应位本身不可靠的可能性就越大。我们利用 l= 5次测量的可靠性信息，对四路PUF实施了基于可靠性的CMA‐ES攻击。该攻击的效率低于传统CMA‐ES攻击，大约需要4,000个挑战‐响应对。尽管如此，结果表明基于可靠性的CMA‐ES攻击在实际中是可行的。对于更多异或门的情况，基于可靠性的攻击显著优于传统的机器学习算法。为了验证这一点，我们将四路PUF的两个连续响应位进行异或运算，从而有效地将四路PUF转变为八路PUF。由于异或门带来的非线性增强以及不可靠性增加，当异或门数量增多时，传统机器学习攻击所需的挑战‐响应对数量大幅上升。使用LR机器学习算法攻击八路 PUF需要300,000个挑战‐响应对，而相比之下，基于可靠性的CMA‐ES攻击仍然仅需4,000个挑战‐响应对。

548 G.T.贝克尔

这一结果乍看之下可能令人惊讶，因为与四路PUF相比，所需的挑战‐响应对数量完全没有增加。但在针对n路PUF的基于可靠性的机器学习攻击中，适应度函数将每个单独响应的可靠性相加，而非进行异或运算。因此，异或门的数量对机器学习算法的影响较小。事实上，即使通过将四路PUF的5个连续位进行异或运算来构建20路PUF，我们仍然可以使用4,000个挑战‐响应对成功实施攻击。
该20路PUF的可靠性仅约为63.1%，因此在实际应用中并不可行。然而，基于可靠性的机器学习攻击仍能为该20路PUF找到模型准确率为61.1%的PUF模型。而该攻击下底层四路PUF的实际模型准确率仍高达约87%。因此，与传统的机器学习攻击不同，增加n路PUF中的异或门数量并不能提升其机器学习抗性。

5.2 攻击XORPUF

最流行的强PUF设计不是n路PUF，而是异或PUF，其每个异或门使用不同的仲裁器PUF。每一个额外的异或门还会增加需要建模的参数，此外还增强了异或的非线性特性。这导致每增加一个异或门，所需的挑战‐响应对都会呈指数增长。因此人们认为，如果使用足够多的级数和异或门，异或PUF可以抵御机器学习攻击[12,28]。然而，在下文中我们将展示，即使被认为是安全的异或 PUF实例，也可以通过基于可靠性的机器学习攻击来攻破。
对于一个 n‐异或、 k‐级的PUF，在机器学习攻击中需要确定(k+ 1) · n个参数。然而，在基于可靠性的机器学习攻击中，可以采用分而治之策略，分别对每个仲裁器PUF进行攻击。这将一次机器学习运行中需要逼近的参数数量减少到仅 k+ 1个。这正是基于可靠性的机器学习攻击在异或PUF上显著优于其他机器学习攻击的主要原因。分而治之方法的核心思想是：响应位的可靠性均等地依赖于所使用的 n个仲裁器PUF。假设对于某个PUF模型 w和其中一个˜ n仲裁器PUF的挑战 Φi，预期的可靠性较低，即 hi= 0。那么测得的可靠性hi也应该较低，因为参与异或运算的任一响应位发生翻转，都会直接导致异或 PUF输出位的翻转。因此，在这种情况下，测得的可靠性 hi与计算出的可靠性˜ ˜hi相匹配。如果挑战 Φi的计算出的可靠性较高，即 hi= 1，且观测到的可靠性也较高，则计算出的可靠性向量与观测到的可靠性向量彼此匹配。然而，其余 n−1个仲裁器PUF中的某一个在此特定挑战下可能是不可靠的。因此，尽管我们的假设认为响应是可靠的，但有时仍可能观察到不可靠的响应。但由于˜我们总是能正确猜测到不可靠的情况，因此即使不完全匹配，假设向量 h仍然与观测到的可靠性向量 h相关。由其他 n−1个仲裁器PUF引入的不可靠性因此被削弱。
承诺与现实之间的差距：论XOR54的安全性问题 9
从机器学习的角度来看，这些只是噪声而已。由于CMA‐ES机器学习算法结合相关系数作为适应度函数对噪声具有很强的鲁棒性，因此CMA‐ES算法仍能为被测仲裁器PUF找到精确的PUF模型。因此，在本次攻击中，我们并非同时针对所有仲裁器PUF，而是逐个建模一个仲裁器PUF。这正是我们的攻击在异或门数量增加时具有良好可扩展性的主要原因。每个额外的仲裁器PUF仅会为计算增加额外的噪声。此外，随着异或门数量的增加，单个异或门带来的相对噪声增量会减小。因此，机器学习攻击的复杂度仅随添加的异或门数量线性增加。
唯一剩下的问题是，我们如何从异或PUF所使用的仲裁器PUF集合中针对一个特定的仲裁器PUF。构建异或PUF基本上有两种方式：要么将相同的挑战应用于所有仲裁器PUF，要么为每个仲裁器PUF提供不同的挑战。经典XOR PUF对所有仲裁器PUF使用相同的挑战。但来自[29]的结果表明，为每个P UF使用不同挑战会使机器学习攻击更加困难。让我们首先考虑每个独立的仲裁器PUF拥有自己一组独特挑战的情况。在这种情况下，攻击者可以根据其在机器学习攻击中使用的挑战来针对特定的仲裁器PUF。由于每个仲裁器PUF具有一组不同的挑战，因此可以逐个攻击各个仲裁器PUF。因此，要攻击一个 n‐XORPUF， n需执行 n次基于可靠性的机器学习攻击。在找到所有PUF的 PUF模型后，整个异或PUF可以通过简单地对各个响应进行异或操作来建模。
CMA‐ES机器学习算法是一种非确定性算法，有时无法收敛到近最优解。在这种情况下，需要重新启动该算法。未能找到准确的PUF模型（即未成功收敛）的机器学习运行，其适应度值远小于成功的运行。因此，可以使用相关系数来检验一次机器学习运行是否成功。如果成功，则可转向下一个PUF；否则应使用相同的挑战重新启动机器学习算法。为了测试这一点，我们通过假设各个仲裁器PUF中每个阶段延迟参数 δ服从随机高斯分布，对不同的XORPUF进行了仿真。假设高斯分布是常见的做法（例如在[29]中使用），并且从安全角度来看代表了一种最佳情况。为了建模噪声的影响，向每个计算出的延迟差异 ΔDP UF添加一个服从 norm(0, σnoise)高斯分布的随机变量。挑战是随机生成的，所有仿真均使用MATLAB完成。为了加快计算速度，针对PUF计算和攻击中计算开销较大的部分，用C语言编写了MEX函数，并在具有4个节点、每个节点64个核心的AMDOpteron集群上运行攻击。每次攻击仅使用16个核心，因此在集群上总共可同时运行16次攻击。现在考虑将相同挑战应用于所有仲裁器PUF的情况，这正是经典XOR‐仲裁器PUF所采用的方式。在这种情况下，攻击者无法通过不同挑战来针对特定的仲裁器PUF，因为所有PUF接收到的挑战都相同。然而，其概率特性

550 G.T.贝克

表2.基于可靠性的CMA‐ES在不同模拟的 n‐XOR、128级PUF上，噪声水平为σnoise= 1的结果。在上方的行中，每个仲裁器PUF使用不同的挑战，而在下方的行中，使用与经典XORPUF相同的方式采用相同的挑战。结果是10次独立攻击的平均值。“单个仲裁器准确率”是指单个仲裁器PUF达到的最大和最小模型准确率。

#异或门可靠性	#挑战‐响应对	准确性 参考集 训练集	准确性	运行次数 每个异或	准确性 单仲裁器	Time
1	98.0%	20 · 103	99.0	98.3	8.7	0.9小时
4	92.5%	150 · 103	97.6%	94.6%	4.0	99.0%–99.3%
8	86.2%	300 · 103	95.3%	89.0%	3.4	98.6%–99.7%
16	76.0%	500 · 103	90.8%	80.2%	19.4	98.7%–99.6%
32a	63.7%	2000 · 103	83.6%	68.4%	9.5	99.1%–99.6%
4	92.5%	150 · 103	97.7%	94.2%	4.2	99.1%–99.7%
8	86.2%	300 · 103	95.7%	89.1%	7.2	99.1%–99.7%
16b	76.1%	500 · 103	90.0%	80.1%	30.6	98.7%–99.6%

a此行仅使用了3次独立攻击的平均值，而非10次
b对于经典的16‐XORPUF，采用了两步法，其中前13个 PUF使用基于可靠性的攻击，其余3个PUF使用传统的CMA‐ES攻击。“#runsperXOR”是由基于可靠性的攻击确定的13个PUF的平均值。

表3.在不同噪声值 σnoise下对8异或、128级PUF进行基于可靠性的CMA‐ES攻击的结果。每个条目均执行了10次攻击。

σnoise	可靠性 单仲裁器	可靠性 异或PUF	#挑战‐响应对	准确性 参考集	运行次数 每个异或	准确性 单仲裁器	Time
0.1	99.8%	98.4%	2500 · 103	96.0%	6.8	98.9%–99.7%	16.7小时
0.25	99.5%	96.2%	1000 · 103	95.5%	8.1	97.2%–99.8%	17.0小时
0.5	99.0%	92.6%	500 · 10 3	94.7%	7.5	98.9%–99.8%	6.6小时
1	98.0%	86.2%	300 · 10 3	95.3%	3.4	98.6%–99.7%	3.3小时
2	96.0%	75.8%	200 · 10 3	94.5%	1.6	98.8%–99.6%	1.2小时
4	92.1%	62.7%	100 · 10 3	84.6%	8.5	96.2%–98.2%	4.6h

CMA‐ES在此情况下对我们有所帮助。基于可靠性的机器学习算法将收敛至异或PUF中的其中一个仲裁器PUF，因为正确PUF模型的相关系数高于不准确 PUF模型的相关系数。如果该机器学习算法总是收敛到同一个PUF，则这种攻击效果不会很好。然而，由于CMA‐ES的概率特性，即使使用相同的输入，该算法在不同的运行中也会收敛到不同的PUF。该攻击的思想是执行尽可能多的独立的机器学习运行，直到找到所有 n个不同的PUF模型。理想情况下，每一次运行找到 n个仲裁器PUF中每一个的可能性应当相等。但在实践中，对于给定的挑战和可靠性向量，某些仲裁器PUF“更容易”而某些“更难”被攻击。因此，该机器学习算法更频繁地收敛到某些PUF实例而非其他实例。
承诺与现实之间的差距：论XOR55的不安全性 1
实际上，攻击者在使用基于可靠性的机器学习攻击时，并不一定需要找出所有的 n物理不可克隆函数。如果只剩下少数几个仲裁器PUF，攻击者可以使用传统的LR或CMA‐ES机器学习攻击来找到剩余的PUF模型。当仅剩少数 PUF时，机器学习攻击很可能收敛到一个已经被建模的PUF。因此，这种两步法可以显著减少对具有大量异或门的PUF（例如16‐XORPUF）的攻击时间。通常情况下，失败的运行可以提前中止，从而大大降低攻击的计算时间。为了判断哪些运行可能失败，可以结合全局突变参数 σ和适应度值进行判断。此外，还可以利用被测模型与已计算出的PUF模型之间的响应汉明距离，来检测那些正在收敛到已发现PUF模型的运行过程。这些运行也可以提前中止，从而显著加快计算速度。基于可靠性的机器学习攻击结果总结于表2中。实验采用的噪声水平为 σnoise= 1，这使得128级仲裁器PUF的可靠性达到98%。这是对仲裁器 PUF可靠性的保守估计。作为对比，在[14]中观测到的64级仲裁器PUF在标称工作条件下的不可靠性约为97%。通过这种新攻击方法，即使是对32‐XOR PUF，也仅需200万组挑战‐响应对即可成功攻击，而使用传统LR则无法实现。
我们还测试了更高或更低可靠性的PUF上的攻击效果。该实验的结果汇总于表 3中。对于非常可靠的PUF，虽然需要更多的挑战‐响应对，但攻击仍然有效。
为了通过实际测量验证这些结果，我们通过从最多8个不同的PUFRFID标签采集测量数据，并将其对应的输出位进行异或运算，从而仿真了一个XORPUF结构。这种方法有效地将四路PUF标签转变为n路与XORPUF的混合结构。在 8‐XOR‐4路PUF中，8个不同的四路PUF经过异或运算，单个响应位总共涉及 32个异或门。该实验的结果见表4。实验表明，使用40万组挑战‐响应对即可成功攻击8‐XOR‐4路PUF。因此，我们的基于可靠性的XORPUF机器学习方法在真实硅数据上同样有效。

表4.基于可靠性的CMA‐ES在使用 l= 5次来自基于PUF的RFID标签的重复测量的 n‐异或四路PUF结构上的结果，其中每个四路PUF使用了不同的挑战。

#物理不可	克隆函数#	异或门#挑	战‐响应对可靠	性准确性 参考集训练集四向	准确性	准确性时间
1	4	4 · 10 3	87.5%	87.1%	88.6%	87.1	0.7米
2	8	10 · 10 3	80.0%	78.5%	80.3%	88.0%	1.6米
4	16	40 · 10 3	69.2%	67.2%	69.4%	87.9%	1.7米
8	32	400 · 10 3	56.3%	55.6%	56.4%	87.5%	13.1米

552 G.T.贝克尔

这表明，对于基于可靠性的机器学习攻击而言，随着异或门数量的增加所需响应数量的指数增长并不成立。与之前所述不同，无论使用的参数如何，普通异或物理不可克隆函数都是不安全的。

6 讨论

在本文中，我们表明强物理不可克隆函数的安全性仍然严重不足。这一点对于商用物理不可克隆函数以及科学界提出的强物理不可克隆函数方案均成立。大量研究工作集中在寻找不同的物理不可克隆函数架构上。然而，我们仍远未充分理解机器学习攻击的全部能力，特别是当使用的信息不仅仅是简单的响应位时。新提出的基于可靠性的CMA‐ES攻击正是这一问题的典型例证。
基本上，为了防止基于可靠性的CMA‐ES攻击，攻击者不应能够两次发送相同的挑战并观察响应的可靠性。如果挑战由标签和验证者共同生成，则可以实现这一点。然而，这通常意味着验证者需要一个PUF的软件模型。此类协议的提案已经提出，例如纤细PUF协议[25]。但是，如果需要软件模型，PUF的若干关键特性将会丧失。例如，“不可克隆性”特性将丢失，因为任何拥有该软件模型的人都可以创建一个PUF的软件克隆。此外，每个对PUF实例进行认证的实体都必须是可信实体，因为这种软件模型可被视为等同于对称密钥。这样的PUF还违反了[28]中定义的“无保护的挑战‐响应接口”要求，因此根据形式化定义，它不是一个强PUF。另一种防止此类攻击的方法可能是受控PUF的概念[7]。然而，最近的研究表明，可以基于纠错码的辅助数据执行基于可靠性的机器学习攻击[2]。由于受控PUF依赖于纠错码，因此该攻击也直接适用于受控PUF。因此，仅仅使用受控PUF并不能解决此问题。如何构建一种能够抵抗基于可靠性的机器学习攻击的强PUF，因此是一个有趣的开放研究问题。
我们对商用基于物理不可克隆函数的射频识别标签的攻击揭示了这项研究在现实世界中的影响。攻击者只需将射频识别读取器或支持近场通信的智能手机靠近标签约5厘米范围内200毫秒，即可收集足够的挑战‐响应对来构建精确的软件模型。我们验证了当智能卡格式物理不可克隆函数标签被放置在牛仔裤后袋内的钱包中时，仍可被读取。我们展示了可以使用现成组件自制的成本低于25美元的射频识别智能卡模拟器来克隆这些标签。这使得一种电子“扒窃”攻击可以在实时条件下实施。因此，尽管人们对强物理不可克隆函数作为一种安全且轻量的身份验证解决方案寄予厚望，但学术界和工业界似乎仍远未实现这些目标。
承诺与现实之间的差距：论XOR553的不安全性