理解:信息量,熵,微分熵
摘要:
信息量 := (事件发生)不确定的量 := 惊讶程度 := (发生)概率倒数的对数 ,即:
I(x) = −log p(x)
说明:
1. 构造中,对数化是为了变乘除为加减,加负号是为了让信息量成为概率的减函数,且信息量取值非负。
2. 对数底,机器学习取e,单位纳特;通信领域取2,单位比特。
(信息)熵 := (整个样本空间下)随机变量整体不确定的量 := 随机变量取所有可能值包含的信息量 := 信息量的数学期望,即:
离散随机变量 (离散)熵H(X) = E[I(X)] = −∑P(x)logP(x); 其中P(x)为概率质量函数或叫分布律
连续随机变量 *微分熵*h(X) = E[I(X)] = -∫ f(x) log f(x) dx;其中f(x)为概率密度函数;
微分熵不是连续版的熵,而是熵在连续极限下的形式推广,使用需谨慎。
理解 信息论里的 信息量 熵
Qwen3-Max
当然!信息论中的信息量(自信息)和熵是理解“不确定性”与“信息”的基石。下面用直觉、公式和例子帮你清晰掌握。
一、信息量(自信息,Self-Information)
🔍 直觉:
越不可能发生的事件,发生时带来的信息量越大。
- 明天太阳升起?→ 几乎必然 → 信息量 ≈ 0
- 明天陨石撞地球?→ 极罕见 → 信息量极大
📐 数学定义:
I(x) = −logP(x)
对一个事件 ,其发生概率为 ,则它的信息量为:
- 单位:比特(bit,以2为底)、纳特(nat,以e为底)等;
- 概率越小 → 越大;
- 若 (必然事件)→ (无新信息)。
✅ 信息量衡量的是单个事件的“惊讶程度”。
二、熵(Entropy)
🔍 直觉:
熵是“平均信息量”,即随机变量整体的不确定性。
- 抛一枚公平硬币:结果难预测 → 熵高(1 bit);
- 抛一枚两面都是正面的硬币:结果确定 → 熵为 0。
📐 数学定义(离散):
H(X) = E[I(X)] = −∑P(x)logP(x)
对随机变量 ,其概率分布为 ,则熵为:
- 是信息量 的期望值;
- 衡量:描述 所需的最小平均编码长度(香农信源编码定理)。
🌰 例子:
- 公平硬币: bit
- 偏置硬币(90%正面): bit(更可预测,熵更低)
三、关键关系总结
| 概念 | 对象 | 含义 | 公式 |
| 信息量 | 单个事件 | 该事件发生带来的“惊讶度” | |
| 熵 | 随机变量 | 整体不确定性的平均信息量 |
✅ 熵 = 信息量的期望
✅ 熵越高,系统越“混乱”,越难预测
四、为什么重要?
- 数据压缩极限:
无损压缩的平均码长 ≥ 熵(香农第一定理); - 机器学习:
决策树用熵(或基尼不纯度)选择最优分割; - 通信:
信道容量与熵密切相关; - 物理学:
热力学熵与信息熵在统计意义上相通。
一句话总结:
信息量告诉你“一件事有多意外”,熵告诉你“一个系统平均有多不可预测”。
它们共同构成了信息论的起点——用数学度量“信息”本身。
连续随机变量的熵通常指的是微分熵(Differential Entropy),它是信息论中衡量连续随机变量不确定性或信息量的工具。微分熵的定义为:
H(X) = -∫ f(x) log f(x) dx
其中,f(x) 是随机变量 X 的概率密度函数(PDF)。微分熵与离散熵类似,但用于描述连续分布的随机变量。
微分熵的性质
微分熵的值并不总是无穷大,但在某些情况下可能趋于无穷大或为负值。以下是一些关键点:
- 熵值可能为负:微分熵的值可以为负,特别是当概率密度函数 f(x) 的值大于 1 时(例如在较小范围内分布很集中的变量)。这与离散熵始终为非负数不同。
- 熵值可能趋于无穷大:当概率密度函数的分布范围无限扩展(例如正态分布的标准差 σ 趋于无穷大)时,微分熵可能趋于无穷大。这是因为分布越宽广,不确定性越大,熵值也越高。
- 单位的影响:微分熵的单位与概率密度函数的定义有关,通常以“比特”或“纳特”为单位。与离散熵不同,微分熵没有严格的单位定义。
特定分布的微分熵
以下是一些常见分布的微分熵公式:
- 正态分布:H(X) = 1/2 log(2πeσ²)。当 σ 趋于无穷大时,熵值趋于无穷大。
- 均匀分布:H(X) = log(b - a)。区间 [a, b] 越大,熵值越高。
- 指数分布:H(X) = 1 - log(λ)。参数 λ 越小,熵值越大。
结论
连续随机变量的熵是否为无穷大取决于其概率密度函数的分布特性。如果分布范围无限扩展(如正态分布的标准差无限大),熵值可能趋于无穷大。但在实际应用中,微分熵通常用于衡量有限范围内的随机变量不确定性,因此其值并不总是无穷大。
信息论 微分熵
Qwen3-Max
微分熵(Differential Entropy)是信息论中连续随机变量的“熵”推广,但它与离散熵有本质区别——它不是信息量的直接度量,也不能表示编码所需的最小比特数。理解它需要明确其定义、性质与局限。
一、定义
设连续随机变量 的概率密度函数为 ,则其微分熵定义为:
![]()
- 单位:比特(若以2为底)或纳特(若以 为底);
- 形式上类似离散熵,但将求和换成积分,概率质量换成概率密度 。
二、关键性质 vs 离散熵
| 性质 | 离散熵 H(X) | 微分熵 h(X) |
| 非负性 | H(X)≥0 | ❌ 可为负值(如窄高斯分布) |
| 信息意义 | 表示最优无损编码平均长度 | ❌ 不能直接解释为编码长度 |
| 坐标不变性 | 与符号标签无关 | ❌ 依赖变量单位(如米 vs 厘米结果不同) |
| 最大熵分布 | 均匀分布 | 在固定方差下,高斯分布最大 |
📌 核心区别:
离散熵衡量“不确定性”,而微分熵衡量的是概率密度的“集中程度”,缺乏绝对信息意义。
三、为什么微分熵可以为负?
考虑一个非常集中的分布,例如:
- X∼N(0,σ2),其微分熵为:
![]()
- 当
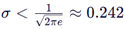 时,h(X) < 0。
时,h(X) < 0。
解释:
密度f(x)可大于1(如尖峰分布),此时 logf(x) > 0,导致−f(x)logf(x) 积分为负。
但这不违反信息论,因为微分熵本身不是“信息量”。
四、微分熵的真正用途
尽管不能直接度量信息,但在以下场景仍有重要价值:
1. 相对比较有意义
- 虽然 绝对值无意义,但差值有意义;
- 例如:互信息 I(X;Y) = h(X) + h(Y) − h(X,Y) 仍非负且有信息意义;
- KL 散度 也有效。
2. 最大熵原理
- 在给定约束下(如均值、方差),使微分熵最大的分布最“无偏”;
- 例:固定方差 → 高斯分布;固定均值(正实数)→ 指数分布。
3. 连续信道容量
- 香农公式 的推导依赖微分熵。
五、与离散熵的关系(极限视角)
若将连续变量X用精度Δ 量化为离散变量 XΔ,则:
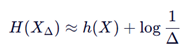
- 当
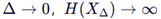 ,(因无限精度需无限比特);
,(因无限精度需无限比特); - 微分熵 = 离散熵减去量化精度带来的发散项。
✅ 这说明:微分熵是“去除无限精度冗余后的相对熵”。
六、常见分布的微分熵

七、一句话总结
微分熵不是“连续版的熵”,而是离散熵在连续极限下的形式推广。
它本身无绝对信息意义,但其差值(如互信息、KL散度)有。
使用时切记:不要将其解释为“平均信息量”或“编码长度”。
它是连接连续概率模型与信息论的桥梁,但必须谨慎解读。




















 1173
1173

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








